Optimal Binary Search Trees

Binary Search Tree 정의

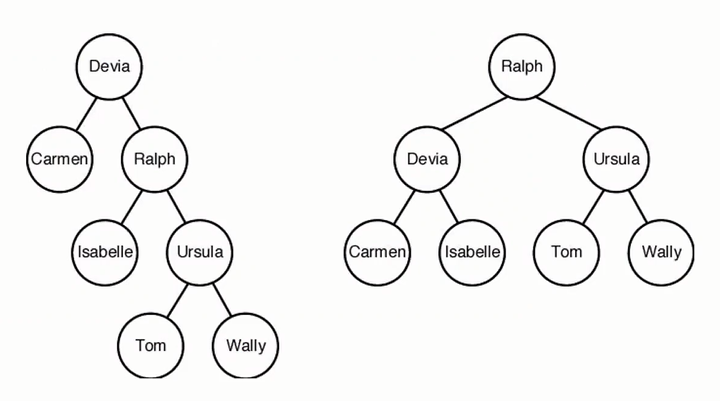
• 값의 중복이 없음
• ordered set(대소 비교 가능한 집합의 원소들) 이 들어온다
• Depth (root는 depth가 0)
• Balanced (depth의 차이가 0~1일경우) ex) 1번 트리는 밸런스 X,2번 트리는 밸런스 O
• Search time = depth+1

그럼 Optimal Binary Search Trees 란

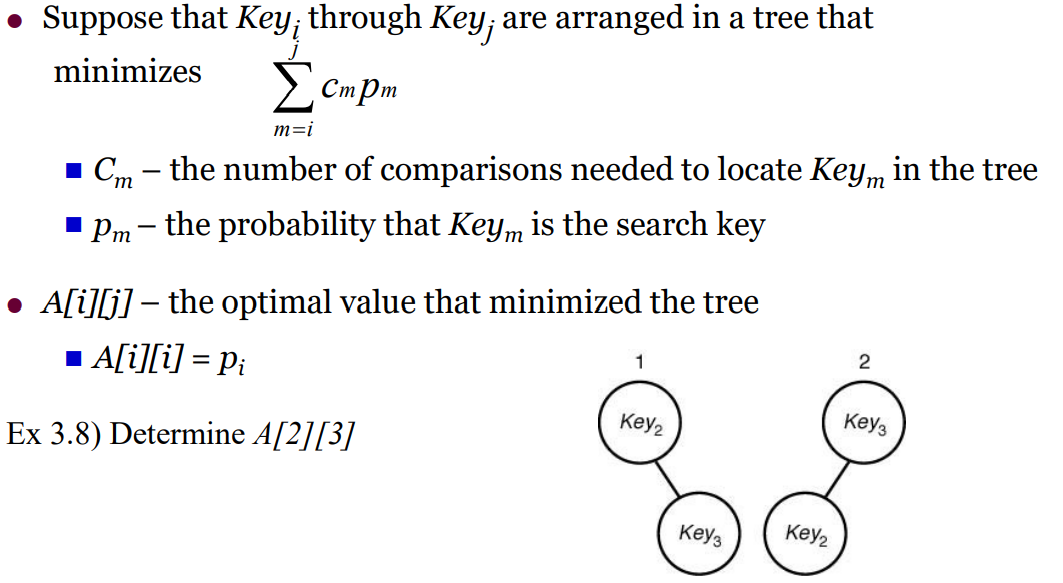
• 평균 탐색 시간이 최소가 되는
  Cm = 비교횟수
  Pm = 단어가 자주 뽑히는 확률
  A = 이진탐색트리를 만드는데 최적 탐색비용의 행렬
  A[i][j] = Ki ~Kj까지 이진탐색트리를 만드는 최적 검색비용
  Ki~kj를 K(i)~K(k-1) K(k) K(k+1)~ K(j) 로 분할하는 재귀 관계식 찾기

즉, 평균 search을 최소화 시키는게 목표!

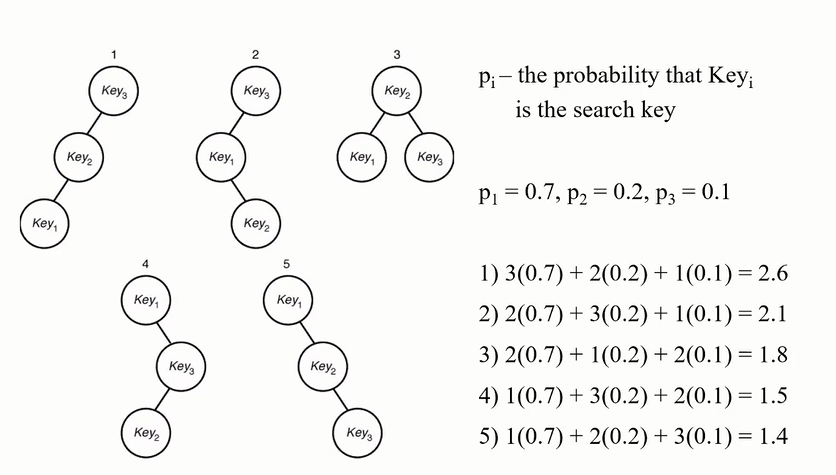
3! 인데 트리 종류는 5개인 이유

• 3번에서 2-1-3 or 2-3-1 두가지가 다 표현되기 때문

DP의 이유

• 어떤 문제의 입력에 대한 최적해가 그 입력을 쪼갠 여러 부분에도 동일하게 최적해가 적용될때.
  (상위트리도, 하위 트리도 똑같은 방식이기 때문) => 최적의 원칙이 적용되기 때문

=> Bottom-Up 으로 풀자

점화식

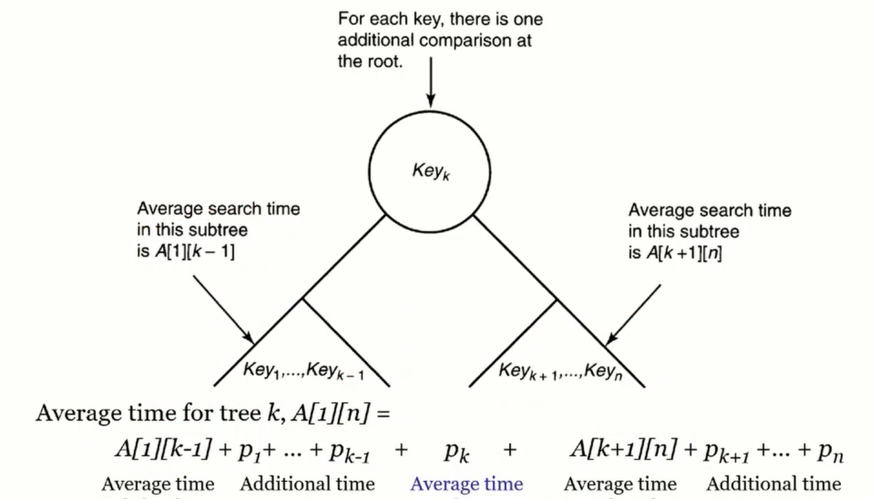
• A[1][k-1] +p1+p2+...+pk + A[k+1][n] +p(k+1)+p(k+2)+...+pn 이다.

p1+...+pn이유

• A[1][k-1] 는 1~(k-1) 일때 평균 서치타임이다.
  근데 root가 k-1 이 아닌 k 임으로 depth는 하나씩 증가하게됨. => 비교횟수가 하나씩 늘어나

• 즉
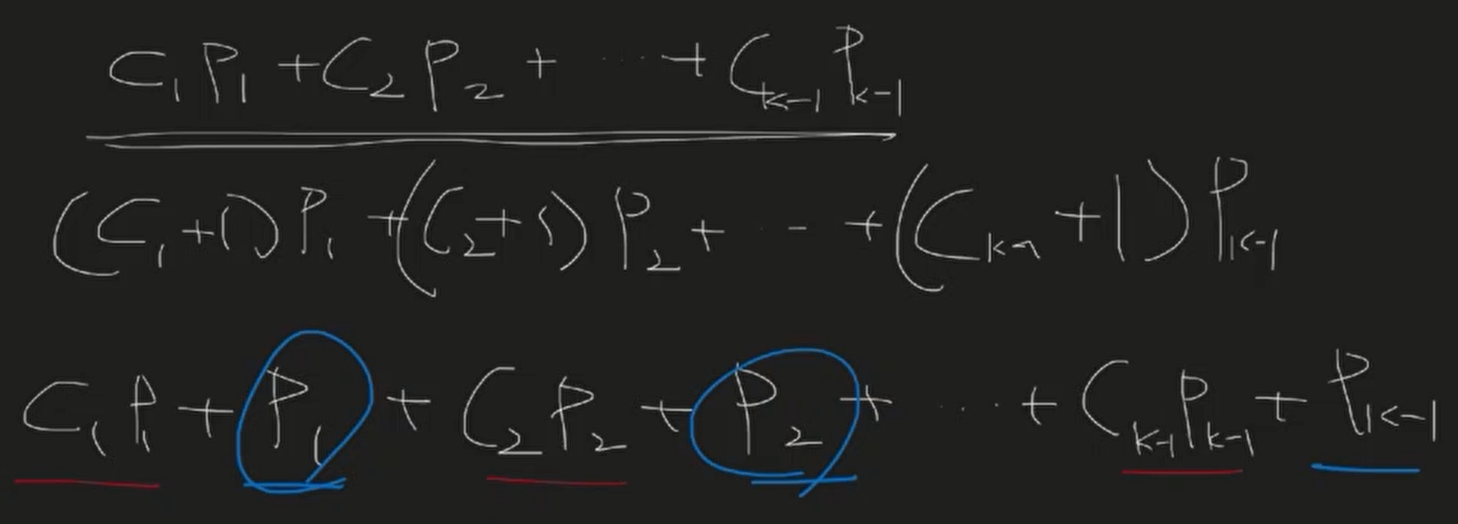
  root가 k가 됨으로서 기존 c1+c2...는 (c1+1)+ (c2+1).. 이 되고
  p1+...+p(k-1) 떨거지가 붙게되는것 + pk(root의 확률) + 반대편...

• 일반화를 한다면
  

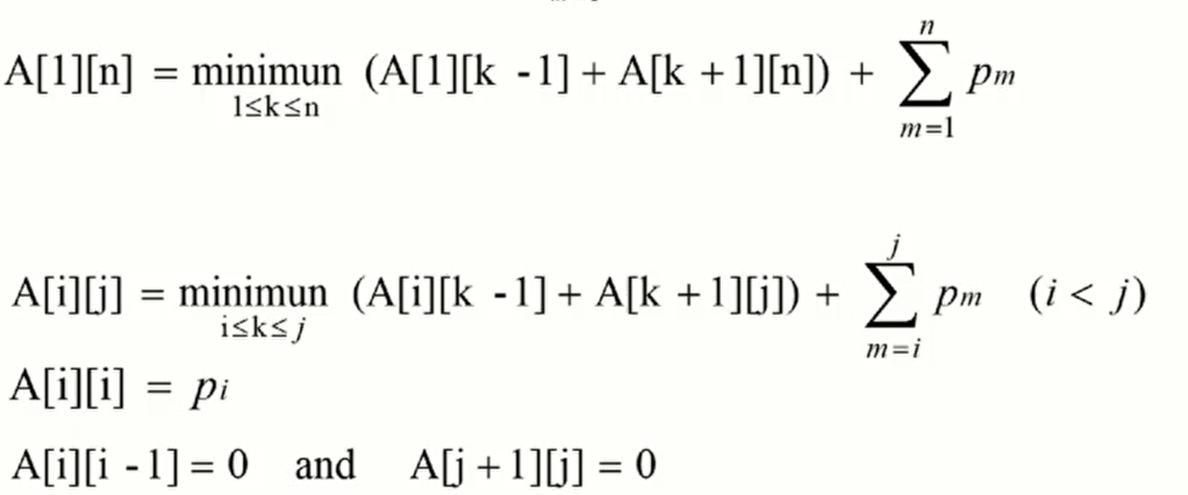
예시

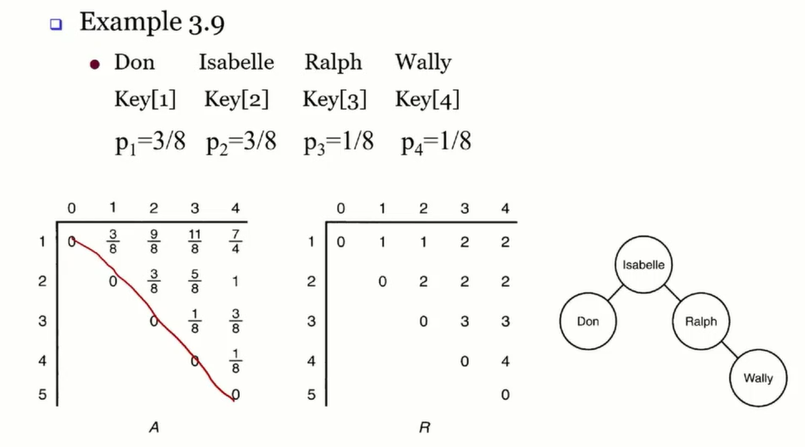
• A[1][0] 같은 경우를 고려하다보니 행은 0~4, 열은 1~5가 나오게 된것

2단계 상향식 방법으로 해답구하기

• 초기화: A[i][i] = p(i)(주대각선을 p(i)로)
• 최종목표: A[1][n]
• A[i][i-1]= A[j+1][j] = 0은 트리의 루트가 맨 끝이여서 왼쪽, 오른쪽이 안나올때
  [i-1] 일때는 행인덱스보다 열인덱스가 하나 더 작을 떄야. A[1][0] 은 말이 안됨으로 0이지

psuedo code

• 필요한건 확률 P배열뿐, R[][] 은 어떤게 루트면 되는지 기록하는 배열
• 3중 loop라서 성능은 O(n^3)
• 원하는 A[1][n] 을 리턴

Ex) R배열의 재귀

• 위 예시에서 R[1][4] = 2
• 2를 루트로 잡고 하면 R[1][1] =1번이 루트 끝, R[3][4] = 3이 루트.
• 3을 루트로 잡고 R[4][4] = 4가 루트

R배열 알고리즘

루트만 계속 결정해주는 재귀