프림 알고리즘은 골랐으면 무조건 soulution set에 넣어. => n-1 회가 무조건 나옴.
사이클 없는 트리에서 vertex가 n개 이기 때문.

반면, 크루스칼은 골랐는데 solution set에 못들어갈 수도 있어서 n-1회보다 많이 돌아.

동작 방식

• 1. weight 순으로 나열해
• v1,v2 연결... v3,v5 연결

• v2,v3는 같은 집합이니 골랐는데 실패
  

수도코드

n= 입력그래프 vertex의 개수
m= 입력그래프 edge의 개수

• 서로소 집합 추상이라는 자료구조 데이터 타입(class)를 임의로 만들고 함수를 사용한것

p= vi가 속한 집합을 찾아라.
q= vj가 속한 집합을 찾아라.

만약 p,q가 같지 않다면,
e라는 엣지를 F에 집어넣고
p집합과 q집합을 합해줘

처음

엣지가 몇개니? n-1 안됐으면 계속 돌아

find,equal,merge,inital 함수 코드설명

inital

• vertex 만큼의 배열 U를 만들고 차레대로 vertex를 넣어.
• 이는 n번 vertex가 n번에 있는 자기자신을 가리켜~ 라는 뜻.

find

• find(1) 하면 return 으로 1이 속한 집합U[1]을 리턴.
• 이는 집합을 대표하는걸 return 한건데. 트리를 대표하는건 root node.
• root 노드는 자기자신을 가리켜.
• root가 다르다는건 집합이 다르다는거 = 트리가 다르다는거

merge

이렇게 2가 1을 가리키는 트리로 변해

U 배열도 이렇게 수정.
같은 root를 가리킨다 = 같은 집합에 있다.

5개의 vertex 가 각각의 집합이었지만,
점점 가다가 find,equal, merge로 마지막에는 하나의 집합으로 합쳐지는 과정

성능분석

• 정렬 할 수 있는 최고의 알고리즘은 O(mlgm)

• 최대 도는 횟수는 O(m). 엣지의 개수만큼

함수들의 오더

inital은 O(n)

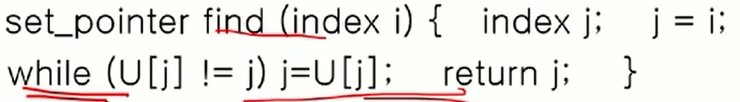
반복문 find가 최악으로 돌 경우 => m번 도는데 O(n)짜리가 안에 있다. => O(mn)

O(n) 인 이유는 선형구조에서 3개일때 비교가 3번, 4개일때 4번....n개일때 n번 비교이기 때문

datastructure 2번으로 바꾸면

노드 개수 n = 2^d(depth 승)
find의 최악의 경우는 = depth +1 = O(lgn)
O(mlgn)

merge 는 O(1) 한번실행.

equal 는 O(1) 한번실행.

최종 성능은 O(mlgm) 엣지들을 정렬하는데 가장 큰 비용이듬.

구현

필요한것

• 1. 간선의 비용을 기준으로 오름차순 정렬
• 2. 각 정점이 포함된 그래프가 어디인지 저장
• 3. 사이클이 발생하지 않는 경우 그래프에 포함

프림 알고리즘과의 차이점

크루스칼

• 모든 가중치를 순차적으로 나열해서 가장 적은 가중치의 간선들을 선택해나감
• 간선 가중치 선택방식
• 간선을 하나씩 선택하는 방식이기때문에 사이클이 나오는지 모니터링해야함
• 간선을 기준으로 정렬하는 과정이 오래걸림
  => 간선 개수 적으면 굳
• O(mlgm)

프림

• 정점을 무지성으로 선택하고 그것과 연결된 가장 적은 비용의 정점을 선택해나감
• 정점 선택방식
• 시작점을 정하고 가까운 정점을 계속 골라가며 트리를 만들어서 사이클 X
• 최소 거리의 정점을 찾는 부분에서 자료구조의 성능에 영향받음
  => 간선 개수 많으면 굳
• O(n^2)