신장트리

• G 안에 있는 모든 정점을 다 포함하면서 트리가 되는 연결 그래프
  (비 순환적, 연결된, 비방향성)이 보장되어야함

MST : 최소 신장 트리

• 모든 신장트리 중에서 가중치의 합이 최소가 되는 신장트리

Brute- Force 방법

• 간선의 개수가 n-1이 될때까지 간선을 하나씩 제거
  트리를 만들면 edge의 개수는 n-1개.
  

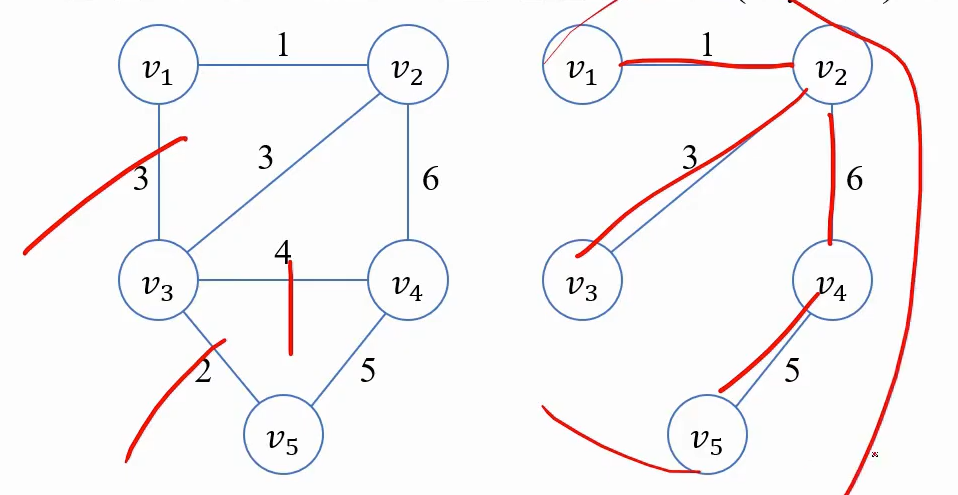
Greedy Approach

프림 알고리즘

High-Level 알고리즘

수도 코드

• nearest[i]. i 는 V-Y 에 있는 얘고,그 값은 Y에 있는 vi랑 가장 가까운 놈을 의미.
  
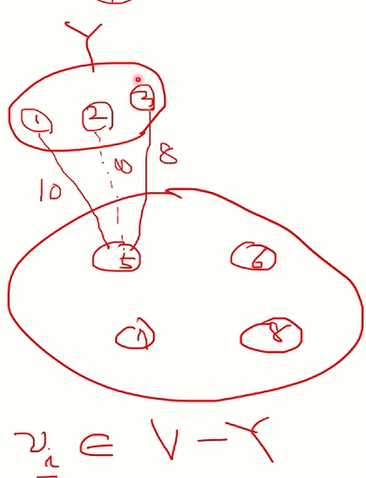
  여기서 nearest[5] = 3이 젤 가까운 vertex.
• distance[5] = 8. 가장 작은 edge weight.

• nearest에서 1은 이미 들어가 있으니까 2~n 까지. Y에 v1은 이미 넣었다고 가정.
  
  Y에 1밖에 없으니 초기화 할때 제일 가까운 nearest은 1이돼.
  distance 는 W[1][i]. 즉 vi와 v1과의 거리

• 새로 편입된 놈들은 vnear에. 그리고 얘네는 -1로 설정해서
  다음 loop를 돌때 0<=distance[i]<= min 에 해당되지 않게 해. => 다음선택을 위한 후처리.

새로 편입된 놈 과 distance[i] 를 비교했을때 새로 편입된 놈이 더 짧으면 그때만 바꿔줘.

성능

루프 두개가 B.O 따라서 2(n-1)(n-1) = O(n^2)