관계대수
1. 관계대수(Relational Algebra)
릴레이션에서 원하는 결과를 얻기 위해 수학의 대수와 같은 연산을 이용하여 질의하는 방법을 기술하는 언어
관계대수와 관계해석
관계대수 : 어떤 데이터를 어떻게 찾는지에 대한 처리 절차를 명시하는 절차적인 언어이며, DBMS 내부의 처리 언어로 사용됨
관계해석 : 어떤 데이터를 찾는지만 명시하는 선언적인 언어로 관계대수와 함께 관계 DBMS의 표준 언어인 SQL의 이론적인 기반을 제공함
→ 관계대수와 관계해석은 모두 관계 데이터 모델의 중요한 언어이며 실제 동일한 표현 능력을 가지고 있음.
관계의 수학적 의미
수학적 개념: ch02 37p 참조
A * B : 집합 A와 집합 B의 각각의 원소들로 만들어낸 모든 조합의 집합
-> (카티전 프로덕트를 집합의 개념으로 본것)
카티전 프로덕트는 뒤에서 설명.
degree(차수)는 더해지고 카디날리티는 곱이 된다!
형식 : R × S
집합에 절댓값 붙으면 집합의 원소 갯수임. 띠용~
카티전 프로덕트 시
degree = abs(a) + abs(b)
cardinarity : abs(a) * abs(b)
abs는 절댓값
+ 재미있는??? 그리스문자 기호 시간~~
통계에서 소문자 시그마 : 표준편차
분산은 시그마의 제곱
퍼져있는 정도가 분산. 루트 씌워서 시그마
셀렉션의 기호도 시그마.
평균은 그리스문자 뮤
영어로 mean이라는 다른 말도 있음
m자로 시작한다
그래서 뮤로 정함.
표준 편차는 영어로 Standard Deviation
따라서 s로 시작해서 시그마.
발음이 s로 시작해서.
소문자와 대문자는 다름.
대문자 시그마는 합. summation
델타는 두가지를 사용한다.
소문자, 대문자.
미분시 소문자. difference
앱실론은 통계, 데이터 분석, 인공지능에서 많이 나옴.
적분 정의할 때 쓰임? 잘 몰루겠다
error. 오륫값 넣을 때 많이 쓰임.
세타 : 쓰레스 홀드. 임계점.
람다 : 람다 계수. 추상화할 때 많이 씀.
오미크론 : 오퍼레이션(연산) 쓸 때 빅 오를 오미크론을 씀.
파이 : 원주율, 대문자 파이는 중복순열 할 때 씀. product의 p를 써서 파이
관계대수 연산자 및 기호
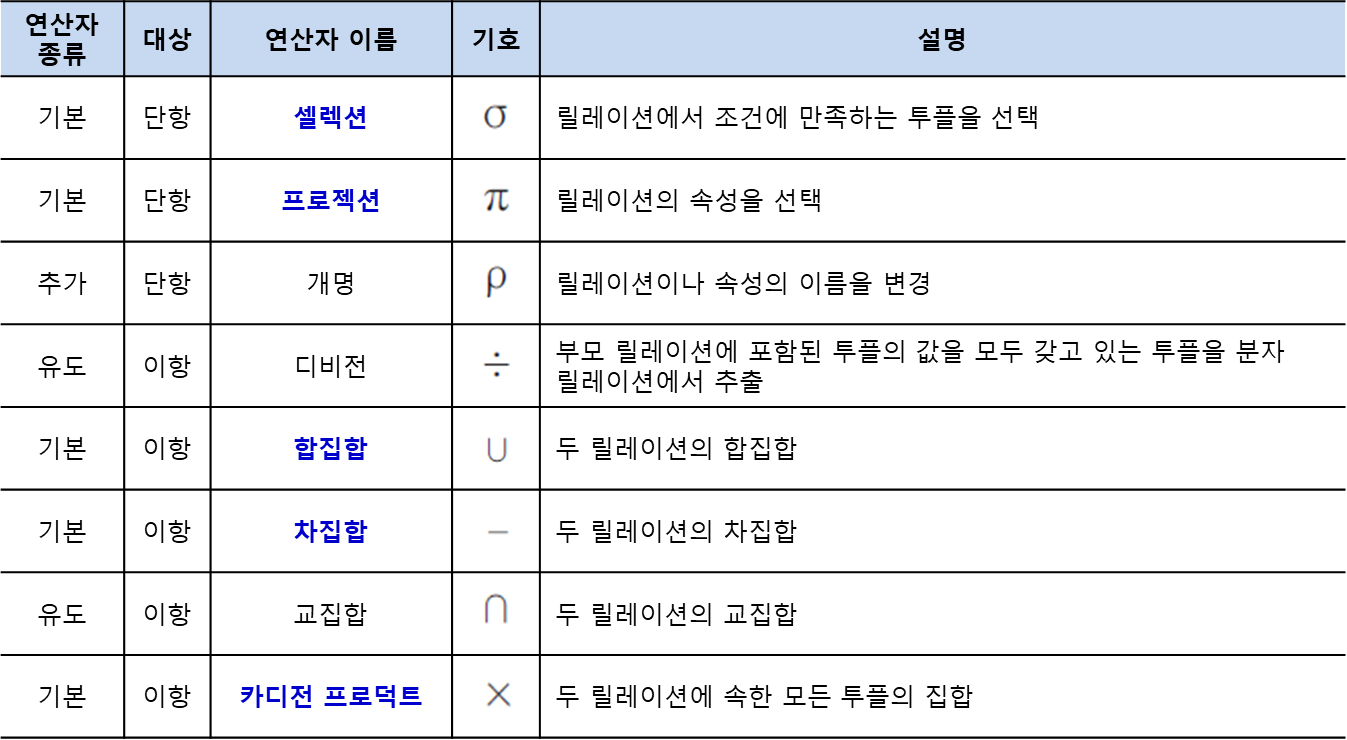
셀렉션 : 소문자 시그마
프로젝션 : 소문자 파이
둘이 유사해서 헷갈릴 수 있음.
rename(개명) : 그리스문자 rho
릴레이션이나 속성 이름을 변경함.
프로젝션은 기벡에서의 프로젝션(정사영)과 유사하다.
프로젝션 보면 축이 3개인데, 2개로 만든 것으로 보면 됨.
이것이 프로젝션과 셀렉션의 차이
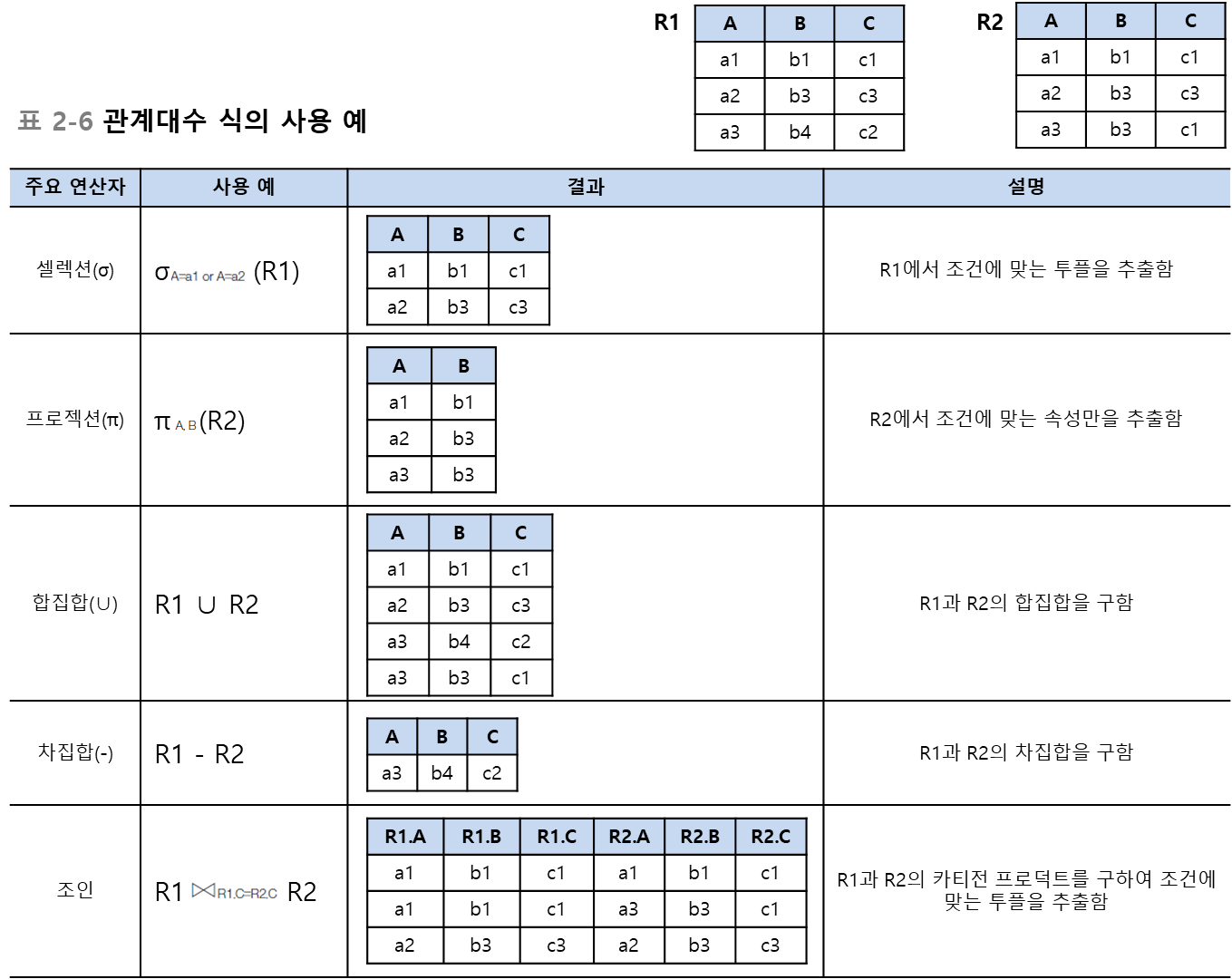
관계대수식
관계대수는 릴레이션 간 연산을 통해 결과 릴레이션을 찾는 절차를 기술한 언어로, 이 연산을 수행하기 위한 식을 관계대수식(relational algebra expression)이라고 함. 관계대수식은 대상이 되는 릴레이션과 연산자로 구성되며, 결과는 릴레이션으로 반환됨. 반환된 릴레이션은 릴레이션의 모든 특징을 따름
단항 연산자 : 연산자<조건> 릴레이션
이항 연산자 : 릴레이션1 연산자<조건> 릴레이션2
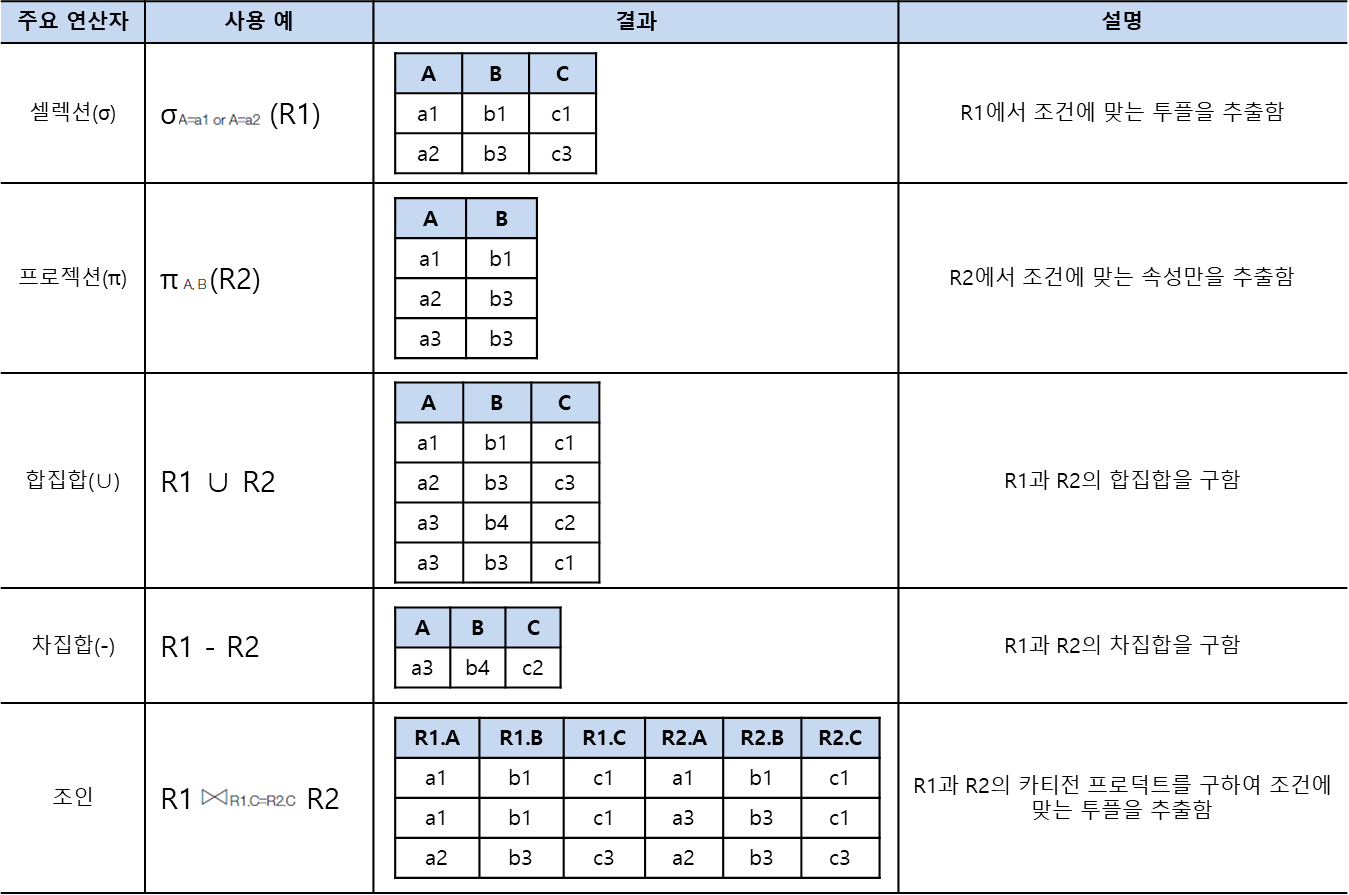
관계대수식의 결과는 위와 같이 항상 릴레이션이다.
2. 셀렉션과 프로젝션
셀렉션
릴레이션의 투플을 추출하기 위한 연산임. 하나의 릴레이션을 대상으로 하는 단항 연산자며, 찾고자 하는 투플의 조건(predicate)을 명시하고 그 조건에 만족하는 투플을 반환함.
-> 셀렉션의 용도는 투플 추출용
SQL 예제
첫 번째 쿼리(셀렉션)
Select *
*=전체 선택
From R1
보통 테이블
Where A = a1 or A = a2
셀렉션의 조건들은 Select가 아닌 Where에 들어간다!
이게 많이 헷갈린다고 함.
셀렉션의 확장
44p 참고
프로젝션
릴레이션의 속성을 추출하기 위한 연산으로 단항 연산자
-> 결과 테이블에 나올 속성(열)들을 선택하는 것
SQL 예제
두 번째 쿼리(프로젝션)
Select A, B
From R2
(Where은 없음)
3. 집합 연산
합집합 : 릴레이션 합치기
교집합 : 릴레이션 공통된것만 남기기
차집합 : 첫번째에만 있는 투플만 남기기
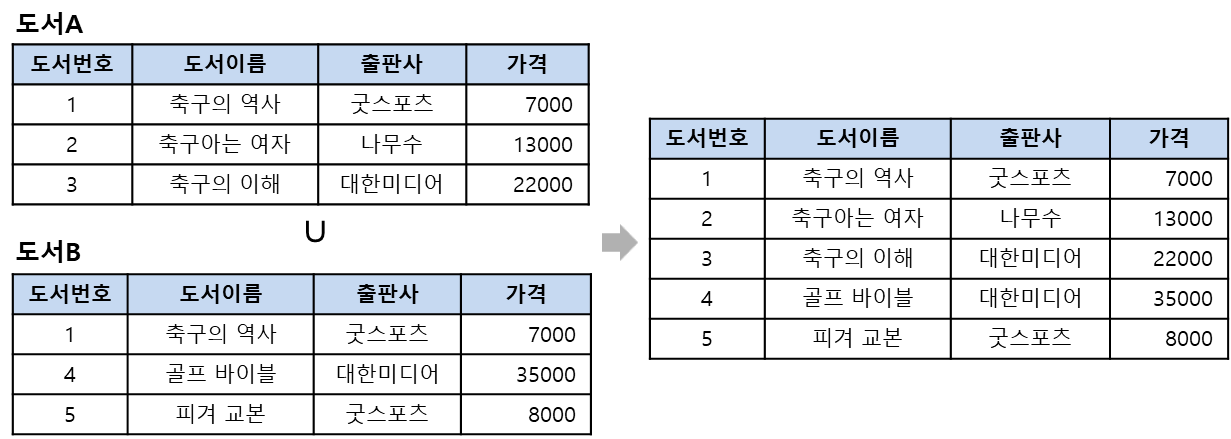
합집합
두 개의 릴레이션을 합하여 하나의 릴레이션을 반환함. 이 때 두 개의 릴레이션은 서로 같은 속성 순서와 도메인을 가져야 함
형식 : R ∪ S
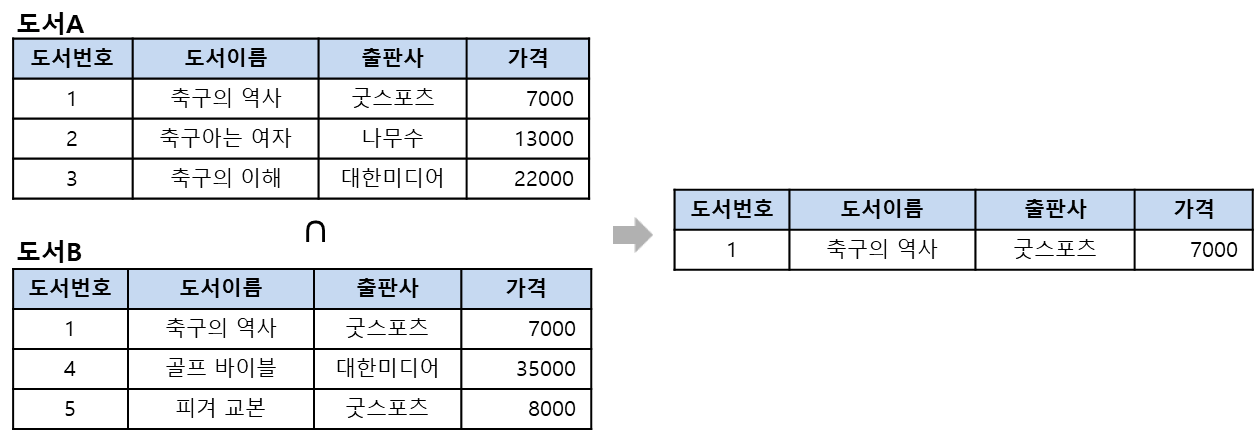
교집합
합병가능한 두 릴레이션을 대상으로 하며, 두 릴레이션이 공통으로 가지고 있는 투플을 반환함
형식 : R ∩ S
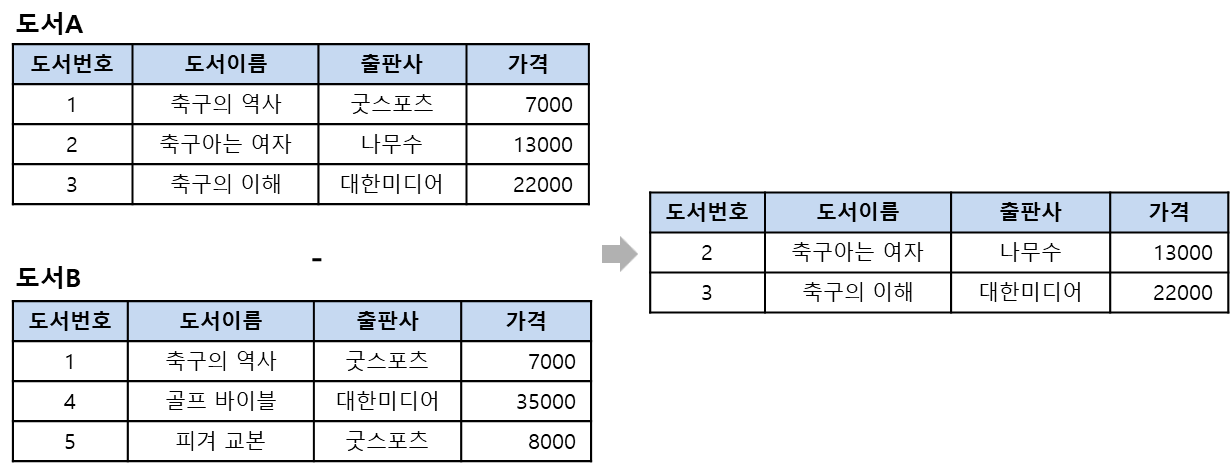
차집합
합병가능한 두 릴레이션을 대상으로 하며, 두 릴레이션이 공통으로 가지고 있는 투플을 반환함
형식 : R - S
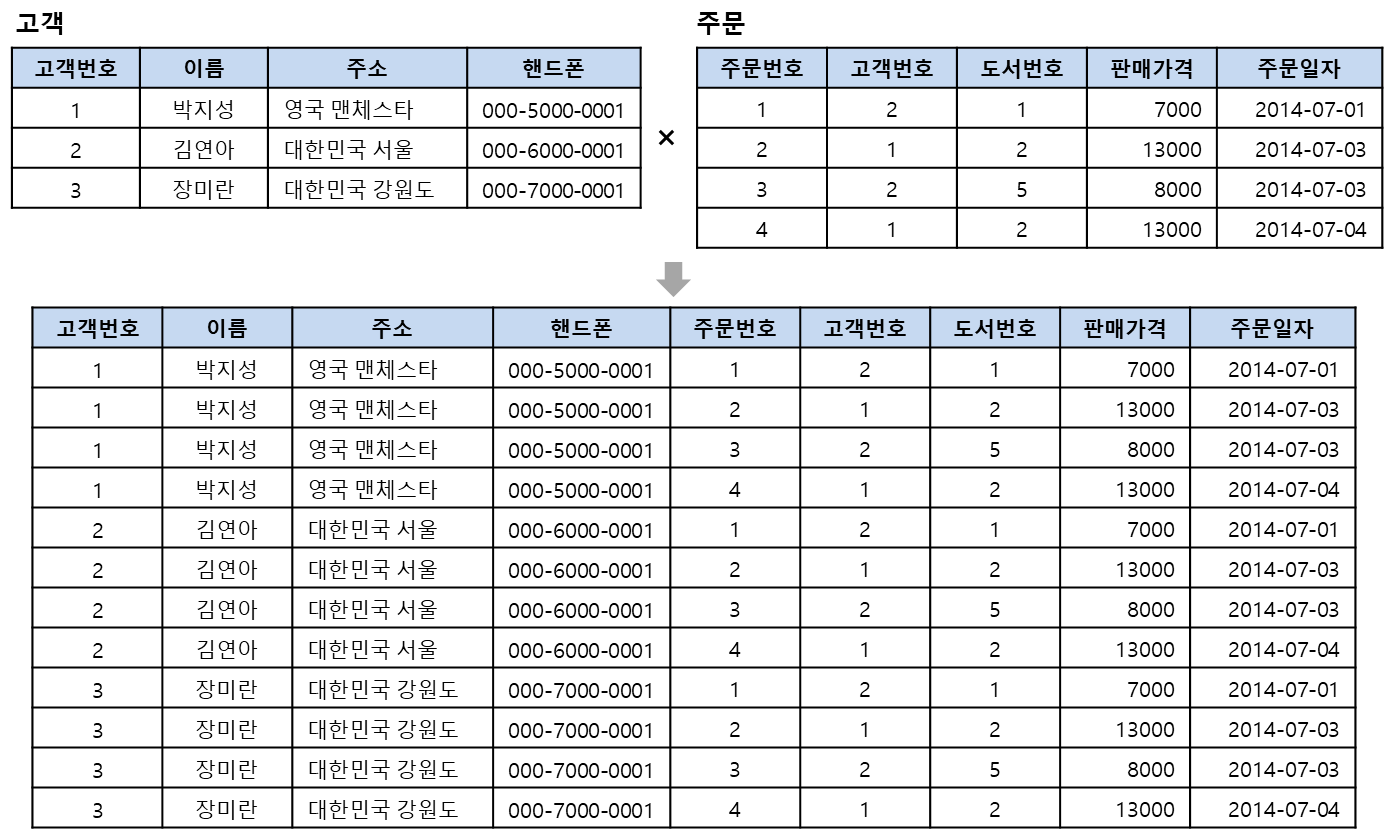
카티전 프로덕트란?
두 릴레이션을 연결시켜 하나로 합칠 때 사용함. 결과 릴레이션은 첫 번째 릴레이션의 오른쪽에 두 번째 릴레이션의 모든 투플을 순서대로 배열하여 반환함. 결과 릴레이션의 차수는 두 릴레이션의 차수의 합이며, 카디날리티는 두 릴레이션의 카디날리티의 곱임
카디날리티 : 테이블의 릴레이션의 객체의 개수
카디날 넘버 : 객체 카운트 넘버?
카디전 프로덕트 : 집합문에 있는 연산
모든 조합을 뽑아내는 것.
카디전 스페이스 : 좌표 공간. 데카르트가 만들었다. 카디전 프로덕트도 데카르트가 만들었다고 한다?
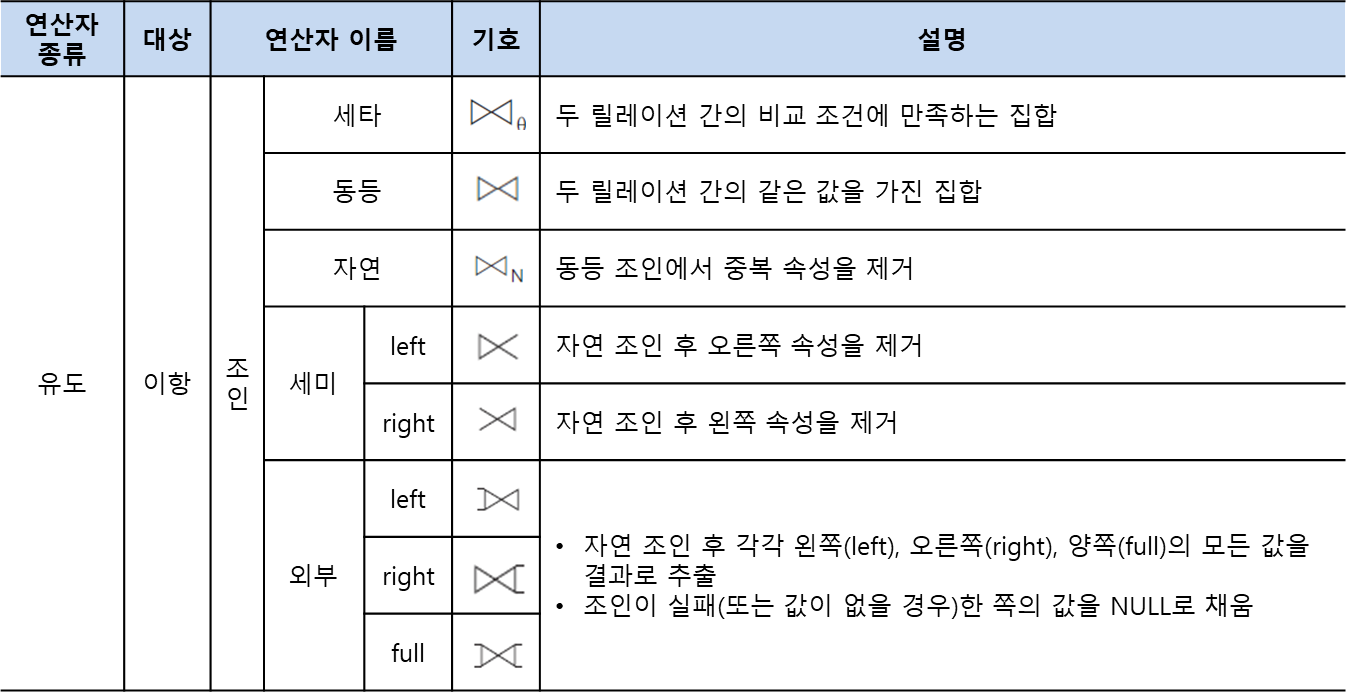
4. 조인
두 릴레이션의 공통 속성을 기준으로 속성 값이 같은 투플을 수평으로 결합하는 연산임. 조인을 수행하기 위해서는 두 릴레이션의 조인에 참여하는 속성이 서로 동일한 도메인으로 구성되어야 함. 조인 연산의 결과는 공통 속성의 속성 값이 동일한 투플만을 반환함.
구분
기본 연산 : 세타조인, 동등조인, 자연조인
확장된 연산 : 세미조인, 외부조인
모래시계 모양은 카디전 프로덕트이나 닫힌 연산을 한다는 뜻임.
세타조인(theta join, θ)
조인에 참여하는 두 릴레이션의 속성 값을 비교하여 조건을 만족하는 투플만 반환함
동등조인(equi join)
세타조인에서 = 연산자를 사용한 조인
동등조인은 세타조인에 포함됨.
-> 실제로 많이 쓰는건 자연조인(natural join)이라고 한다. 근데 왜 설명이 이렇게 나왔지
자연 조인(natural join)
동등조인에서 조인에 참여한 속성이 두 번 나오지 않도록 두 번째 속성을 제거한 결과를 반환함.
-> 중복제거. 어떤것의 중복을 제거? 컬럼의 중복. 일반적으로 조건 안넣고 공통으로 쓰는거 넣음.
공통컬럼 : 고객번호. 고객번호 하나로 모든 조합을 뽑아낸다.
고객번호가 같다? 같은것에대한 degree는 빼준다.
그래서 자연조인은 일반적으로 가장 많이 사용함.
외부조인과 세미조인
left : 왼쪽이 닫힌 연산
right : 오른쪽이 닫힌 연산
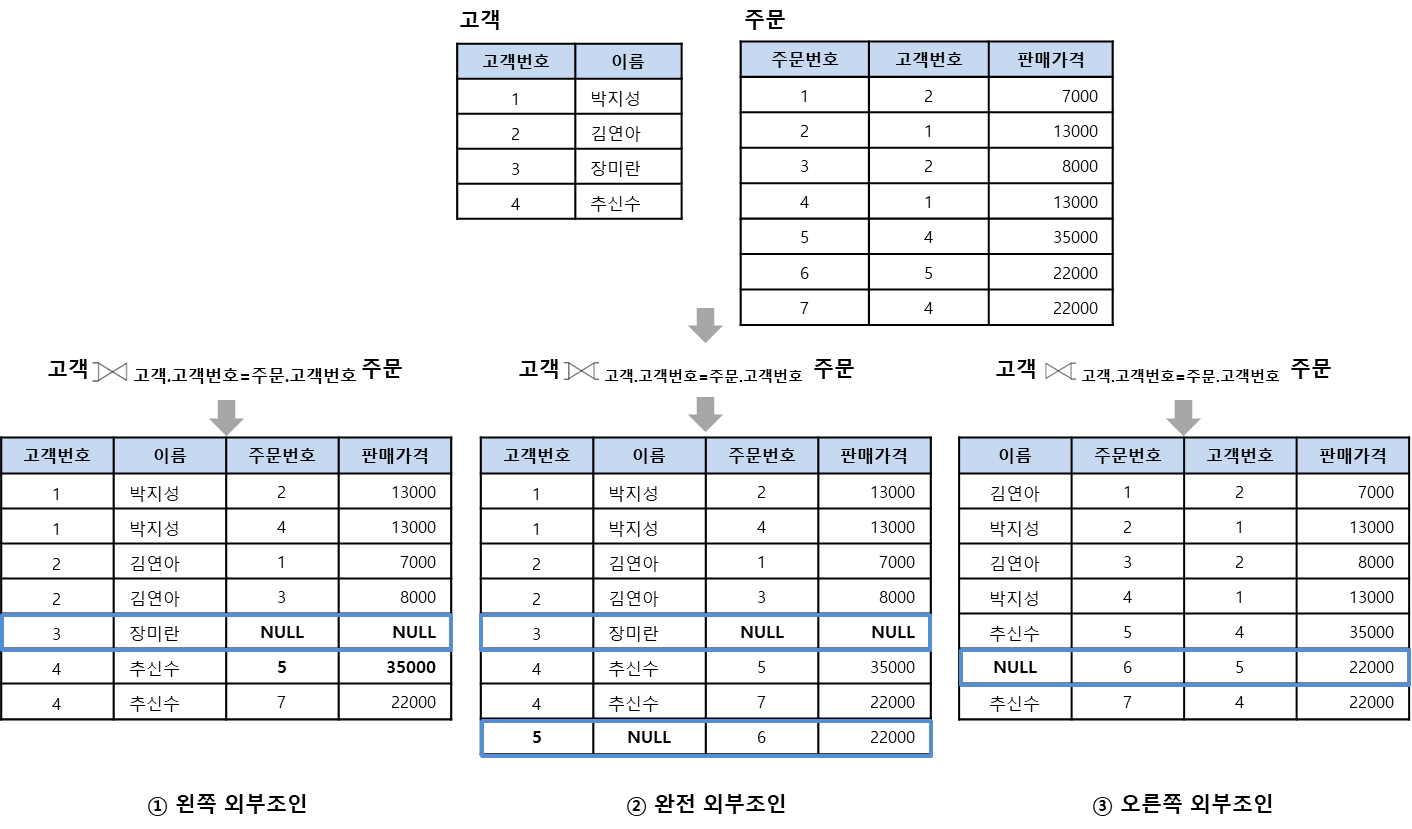
외부조인(outer join)
자연조인 시 조인에 실패한 투플을 모두 보여주되 값이 없는 대응 속성에는 NULL 값을 채워서 반환
모든 속성을 보여주는 기준 릴레이션 위치에 따라 왼쪽(left) 외부조인, 오른쪽(right) 외부조인, 완전(full, 양쪽) 외부조인으로 나뉨
-> 확장해준다는 개념으로 보면 됨.
자연조인은 공통적인 값을 가진 조항만 남긴다.
여기는 아닌 애들도 NULL 값 주고 추가한다?
세미조인(semi join)
자연조인을 한 후 두 릴레이션 중 한쪽 릴레이션의 결과만 반환하며, 기호에서 닫힌 쪽 릴레이션의 투플만 반환함.
-> 조인을 하긴 하는데, 한쪽의 릴레이션만 반환함. 그래서 세미조인이다.
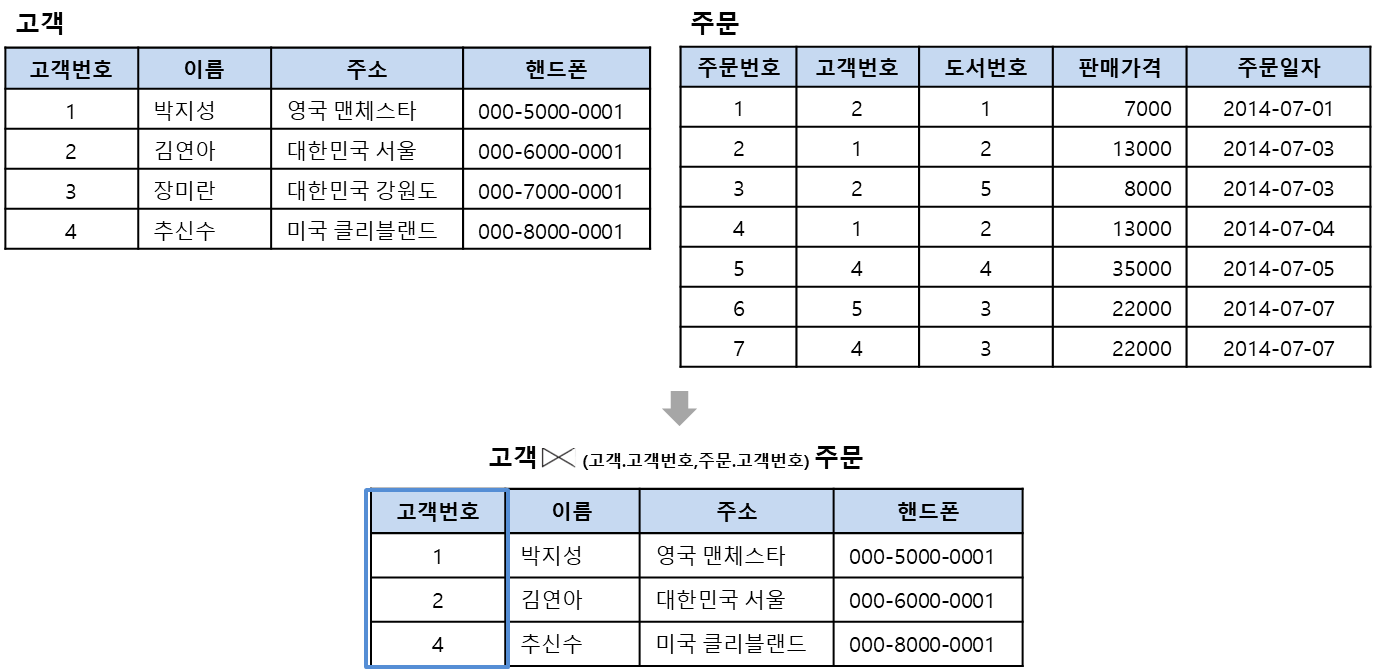
왼쪽이 닫힌 경우의 예
5. 디비전
릴레이션의 속성 값의 집합으로 연산을 수행함
일반적인 수학의 나눗셈 기호와 같다. 그러나 연산은 같지 않다.
부모 릴레이션에 포함된 투플의 값을 모두 갖고 있는 투플을 분자 릴레이션에서 추출
형식 : R ÷ S
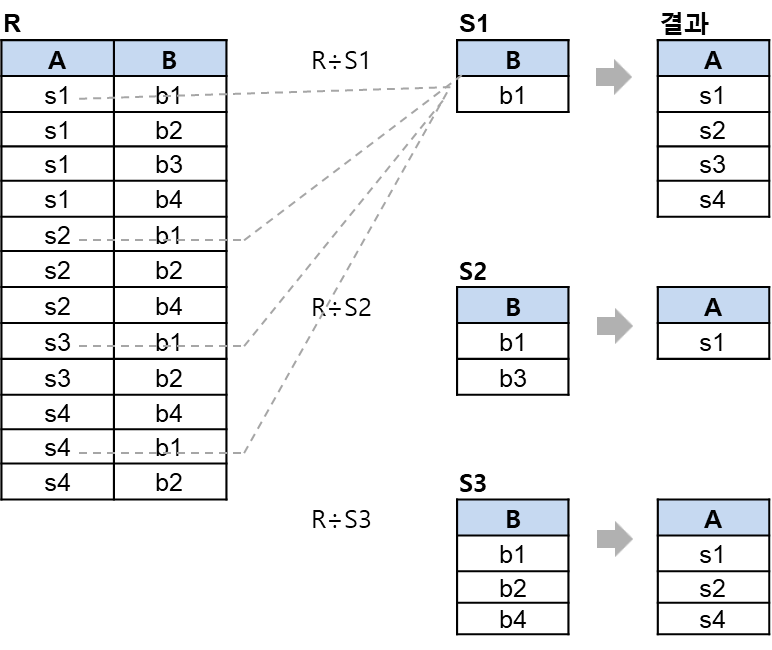
!주의!
R ÷ S2
-> 이 경우 b1,b3를 공통으로 가지고있는 s1만 뽑아짐
R ÷ S3도 동일.
divide or division이란 연산은 없고 group by / grouping 이라는 명령어로 유사하게 처리됨.
+) 덤
카티전 프로덕트를 이용한 연산
명령어 최적화 하기

고객이름을 먼저찾고 거기다 주문을 카티전 프로덕트를 한다.
이 경우 카티전 프로덕트를 할 테이블의 크기가 줄어드므로 실제로는 연산이 더 빨라진다.
이런게 쿼리 옵티마이제이션(optimization)라고 한다.
