문제 출처

단계별로 풀어보기 > 구간 합 > 구간 합 구하기 4
https://www.acmicpc.net/problem/11659

문제 설명

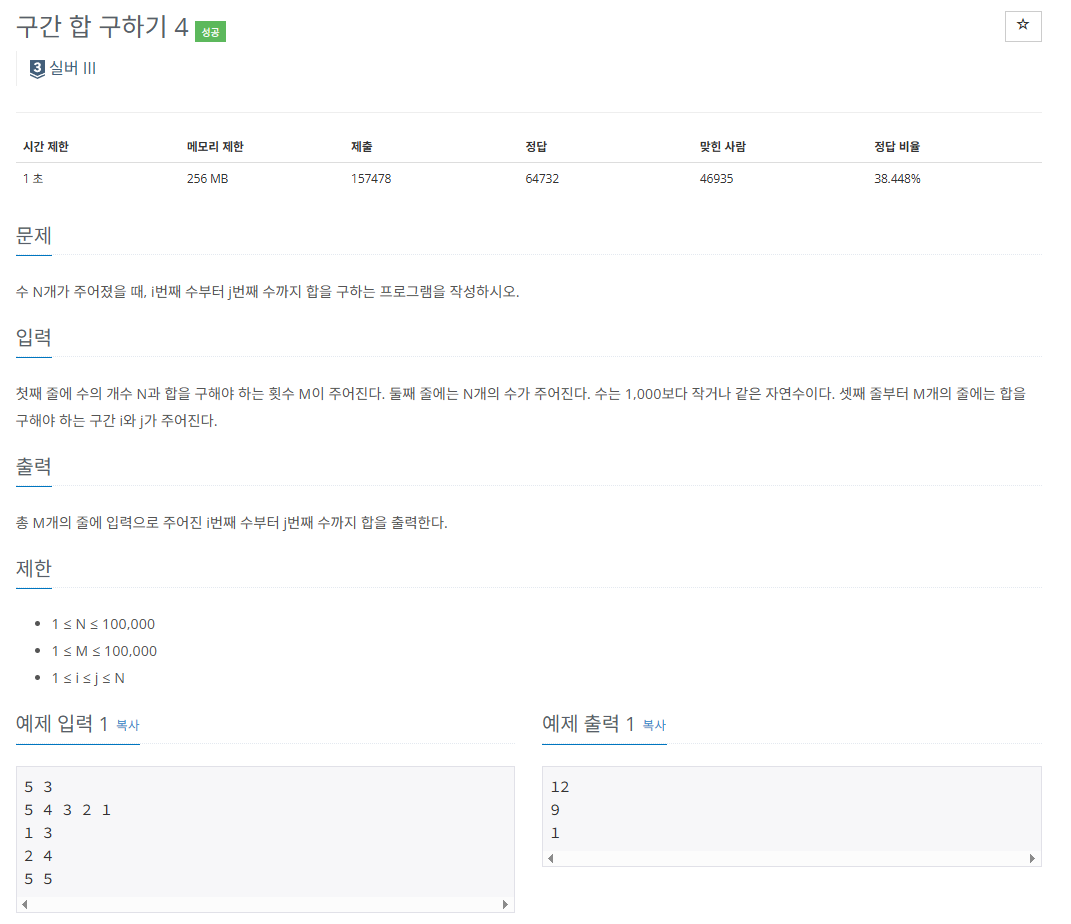
수 N개가 주어질 때, i ~ j 번째 수까지 합을 구하라

접근 방법

N개의 수를 입력받아 배열에 삽입할 때, 각 자리는 해당 자리 수 + 이전까지의 합을 저장한다.
이를 통해 구간이 주어지면, 구간의 마지막 인덱스 - (구간의 시작-1 인덱스)를 통해 해당 구간의 합을 구할 수 있다.

import java.io.*;
import java.util.StringTokenizer;

public class 구간_합_구하기_4 {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());

        int N = Integer.parseInt(st.nextToken());
        int M = Integer.parseInt(st.nextToken());

        int arr[] = new int[N+1];
        st = new StringTokenizer(br.readLine());

        arr[0] = 0;

        for(int i = 0; i<N; i++){
            arr[i+1] = arr[i] + Integer.parseInt(st.nextToken());
        }

        StringBuilder sb = new StringBuilder();

        for(int i = 0; i<M; i++){
            st = new StringTokenizer(br.readLine());

            int a = Integer.parseInt(st.nextToken());
            int b = Integer.parseInt(st.nextToken());
            int sum = arr[b] - arr[a-1];
            sb.append(sum).append("\n");
        }

        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
        bw.write(sb.toString());
        bw.flush();
        bw.close();

    }
}

Review

import java.io.*;
import java.util.StringTokenizer;

public class 구간_합_구하기_4_review {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());

        int N = Integer.parseInt(st.nextToken());
        int M = Integer.parseInt(st.nextToken());

        int arr[] = new int[N+1];

        arr[0] = 0;
        st = new StringTokenizer(br.readLine());
        for(int i = 1; i<N+1; i++){
            arr[i] = arr[i-1]+Integer.parseInt(st.nextToken());
        }

        StringBuilder sb = new StringBuilder();

        for(int k = 0; k<M; k++){
            st = new StringTokenizer(br.readLine());

            int sum = 0;

            int i = Integer.parseInt(st.nextToken());
            int j = Integer.parseInt(st.nextToken());


            sum = arr[j] - arr[i-1];

            sb.append(sum).append("\n");
        }

        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
        bw.write(sb.toString());
        bw.flush();
        bw.close();
        br.close();
    }
}

알게된 점

처음엔 흔히 생각할 수 있는 배열의 구간의 합을 이용해서 풀었지만, 이는 시간 복잡도가 O(NM)이 된다.
이 경우 문제에서의 N과 M의 개수가 각각 100,000 개까지 주어질 수 있으므로,
100,000 100,000 = 10,000,000,000개가 될 수 있어 Java에서 1초에 계산할 수 있는 100,000,000을 넘어간다.

import java.io.*;
import java.util.StringTokenizer;

public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());

        int N = Integer.parseInt(st.nextToken());
        int M = Integer.parseInt(st.nextToken());

        int arr[] = new int[N];
        st = new StringTokenizer(br.readLine());

        for(int i = 0; i<N; i++){
            arr[i] = Integer.parseInt(st.nextToken());
        }

        StringBuilder sb = new StringBuilder();

        for(int i = 0; i<M; i++){
            st = new StringTokenizer(br.readLine());

            int a = Integer.parseInt(st.nextToken()) - 1;
            int b = Integer.parseInt(st.nextToken());
            int sum = 0;

            for(int j = a; j<b; j++){
                sum += arr[j];
            }
            sb.append(sum).append("\n");
        }

        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
        bw.write(sb.toString());
        bw.flush();
        bw.close();

    }
}

그래서 구간 합을 배열에 저장하는 방식을 사용하여 O(N+M)의 시간 복잡도를 챙긴다.

Review
어렵지 않게 풀렸다.

문제푼 흔적

Review