문제 출처

전체문제 > 나는 학급회장이다
https://www.acmicpc.net/problem/2456

문제 설명

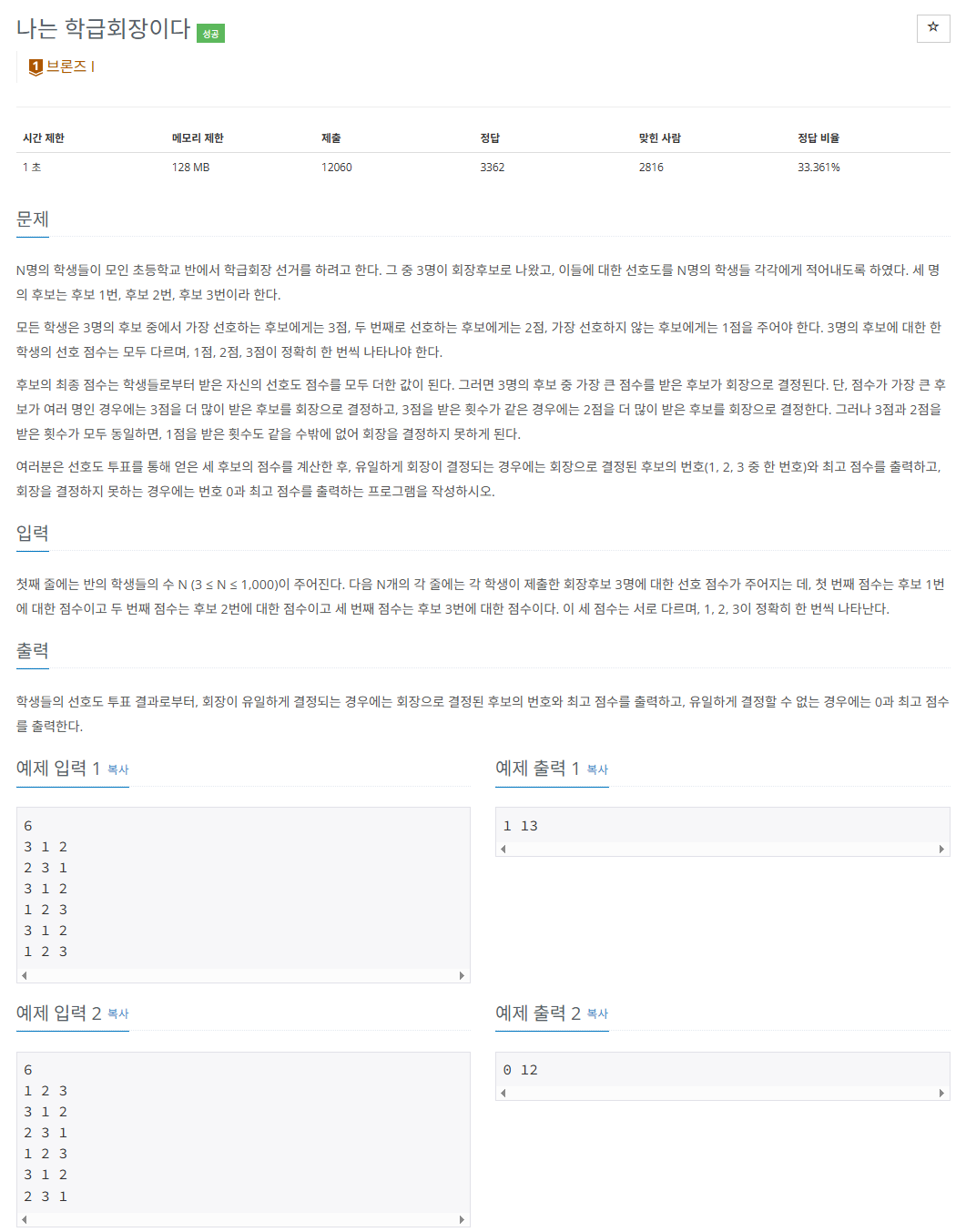
N명의 학생이 있을 때, 그 중 3명의 학급회장을 한 명 뽑는다. 학생들은 각각 선호도 점수 1, 2, 3점을 각 후보에게 점수를 줄 ㅅ수 있다. 전체 점수를 합계했을 때, 후보의 점수가 같다면, 3점이 많은 순서로, 3점이 많은 순서도 같다면 2점이 많은 순서로 회장을 선출한다.
이 때, 후보의 번호를 출력하고, 해당 후보의 점수도 출력하라.(만약 2점의 갯수도 동일하다면 0과 최고 점수를 출력한다.)

접근 방법

반복문을 통해 후보마다. 점수를 합하고, 점수를 합할 때, 해당 점수의 제곱을 기록하는 배열에 제곱한 점수를 따로 더한다.(동점 가르기 용) 이를 통해 가장 큰 점수를 가진 후보를 선출하고, 점수가 동일하다면 제곱을 기록한 배열에서 가장 큰 후보를 확인한다.

import java.io.*;
import java.util.StringTokenizer;

public class 나는_학급회장이다 {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));

        int[] candidate = new int[3];
        int[] squared = new int[3];

        int N = Integer.parseInt(br.readLine());

        for (int i = 0; i < N; i++) {
            StringTokenizer st = new StringTokenizer(br.readLine());
            int a = Integer.parseInt(st.nextToken());
            int b = Integer.parseInt(st.nextToken());
            int c = Integer.parseInt(st.nextToken());

            candidate[0] += a;
            candidate[1] += b;
            candidate[2] += c;

            squared[0] += a * a;
            squared[1] += b * b;
            squared[2] += c * c;
        }

        int maxScore = Math.max(candidate[0], Math.max(candidate[1], candidate[2]));

        if (countOccurrences(candidate, maxScore) == 1) {
            for (int i = 0; i < candidate.length; i++) {
                if (candidate[i] == maxScore) {
                    bw.write((i + 1) + " " + maxScore + "\n");
                    break;
                }
            }
        } else {
            int maxSquared = Math.max(squared[0], Math.max(squared[1], squared[2]));
            int elected = -1;

            for (int i = 0; i < squared.length; i++) {
                if (squared[i] == maxSquared) {
                    elected = i;
                    break;
                }
            }

            if (countOccurrences(squared, maxSquared) > 1) {
                bw.write("0 " + candidate[elected] + "\n");
            } else {
                bw.write((elected + 1) + " " + candidate[elected] + "\n");
            }
        }

        bw.flush();
        br.close();
        bw.close();
    }

    private static int countOccurrences(int[] array, int value) {
        int count = 0;
        for (int v : array) {
            if (v == value) count++;
        }
        return count;
    }
}

알게된 점

처음에는 해쉬맵을 통해 각각 후보가 받은 3점,2점,1점의 갯수를 모두 저장하는 방식으로 생각했었으나, 다른 사람의 풀이를 보고 제곱을 이용하게 된다면, 점수가 동일할 때 3점을 많이 받은 후보가 가장 제곱들의 총합 점수가 높고, 그 다음은 2점을 많이 받은 후보가 되는 방향성을 보고 점수 비교에서 제곱을 사용할 수 있음을 알게 되었다.

출처
https://velog.io/@youngjun_10/%EB%B0%B1%EC%A4%80-%EB%82%98%EB%8A%94-%ED%95%99%EA%B8%89%ED%9A%8C%EC%9E%A5%EC%9D%B4%EB%8B%A4

문제푼 흔적