자료구조 / Binary Search Tree

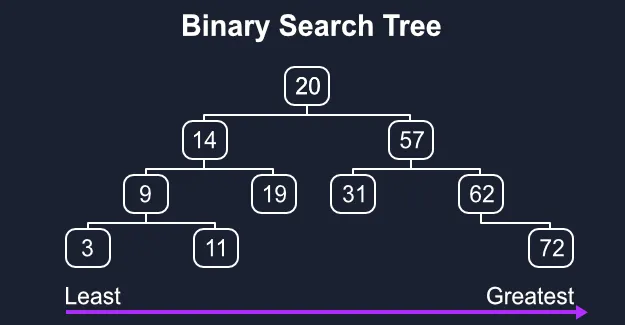
이진 탐색 트리란?

이진 탐색 트리는 각 노드가 최대 두 개의 자식 노드를 가지며, 각 노드의 왼쪽 서브 트리는 해당 노드보다 작은 값들로, 오른쪽 서브 트리는 해당 노드보다 큰 값들로 이루어진다. 이렇게 구성된 트리는 탐색 및 삽입 연산이 빠르게 수행된다.

이진 탐색 트리의 특징

1. 각 노드는 최대 두 개의 자식 노드를 가진다. 각 노드의 왼쪽 서브 트리에는 해당 노드보다 작은 값들이 위치하며, 오른쪽 서브 트리에는 해당 노드보다 큰 값들이 위치한다. 이러한 특성으로 인해 탐색 연산이 빠르게 수행되며 특정 값을 찾을 때, 현재 노드의 값과 비교하여 탐색 방향을 결정할 수 있다.

2. 중위 순회(In-order traversal)를 통해 이진 탐색 트리의 모든 노드를 정렬된 순서로 방문할 수 있다. 따라서 이진 탐색 트리는 정렬된 데이터를 유지하면서 삽입, 삭제, 검색이 가능한 자료구조로 사용된다.

3. 이진 탐색 트리에서의 검색 연산의 시간 복잡도는 O(log n)이며, 이는 트리의 높이에 의해 결정된다. 따라서 큰 데이터셋에서도 효율적으로 탐색 및 정렬이 가능하다.

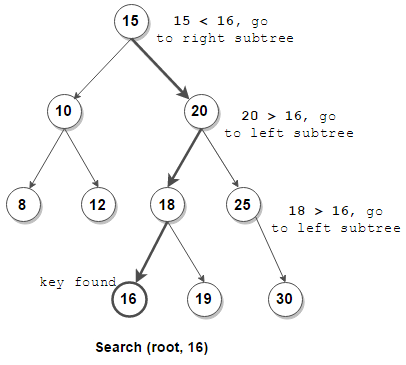
4. 삽입 및 삭제 연산 또한 트리의 높이에 의존하며, 평균적으로 O(log n)의 시간 복잡도를 갖는다. 특정 케이스에서는 트리가 한쪽으로 치우쳐져 불균형한 형태를 갖게 되어 시간 복잡도가 O(n)이 될 수 있다. 따라서 균형을 유지하는 트리 구조(예: AVL 트리, 레드-블랙 트리)를 사용하기도 한다.

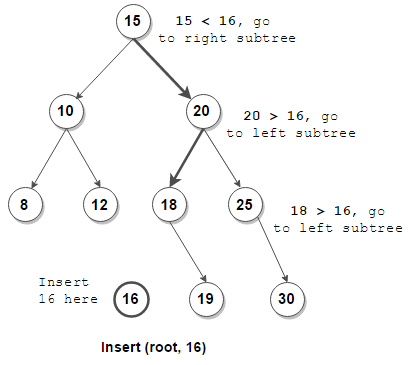
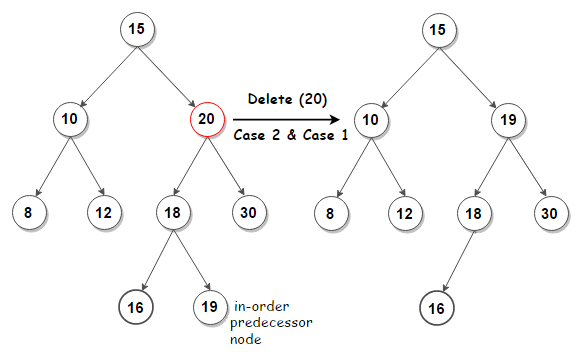
5. 이진 탐색 트리에서 가장 왼쪽에 있는 노드는 전체 트리에서 가장 작은 값이고, 가장 오른쪽에 있는 노드는 가장 큰 값이다. 따라서 최소값 또는 최대값을 찾는 데에도 효율적이다.

6. 이진 탐색 트리는 재귀적인 방식으로 구현이 가능하다. 각 노드는 키 값, 왼쪽 서브 트리, 오른쪽 서브 트리로 이루어져 있으며 삽입, 삭제, 검색 등의 연산을 구현하면서 트리의 균형을 유지하는 것이 중요하다.

이진 탐색 트리 구현

class Node {
    int key;
    Node left, right;

    public Node(int item) {
        key = item;
        left = right = null;
    }
}

public class BinarySearchTree {
    private Node root;

    public BinarySearchTree() {
        root = null;
    }

    // 검색
    public Node search(int key) {
        return searchRec(root, key);
    }

    private Node searchRec(Node root, int key) {
        if (root == null || root.key == key)
            return root;

        if (key < root.key)
            return searchRec(root.left, key);

        return searchRec(root.right, key);
    }

    // 삽입
    public void insert(int key) {
        root = insertRec(root, key);
    }

    private Node insertRec(Node root, int key) {
        if (root == null) {
            root = new Node(key);
            return root;
        }

        if (key < root.key)
            root.left = insertRec(root.left, key);
        else if (key > root.key)
            root.right = insertRec(root.right, key);

        return root;
    }

    // 삭제
    public void delete(int key) {
        root = deleteRec(root, key);
    }

    private Node deleteRec(Node root, int key) {
        if (root == null)
            return root;

        if (key < root.key)
            root.left = deleteRec(root.left, key);
        else if (key > root.key)
            root.right = deleteRec(root.right, key);
        else {
            // 노드가 한 개 또는 없는 경우
            if (root.left == null)
                return root.right;
            else if (root.right == null)
                return root.left;

            // 노드가 두 개인 경우
            root.key = minValue(root.right);

            // 오른쪽 서브 트리에서 후계자 값을 삭제
            root.right = deleteRec(root.right, root.key);
        }

        return root;
    }

    private int minValue(Node root) {
        int minValue = root.key;
        while (root.left != null) {
            minValue = root.left.key;
            root = root.left;
        }
        return minValue;
    }

    // 중위 순회
    public void inOrder() {
        inOrderRec(root);
    }

    private void inOrderRec(Node root) {
        if (root != null) {
            inOrderRec(root.left);
            System.out.print(root.key + " ");
            inOrderRec(root.right);
        }
    }

    public static void main(String[] args) {
        BinarySearchTree tree = new BinarySearchTree();

        tree.insert(50);
        tree.insert(30);
        tree.insert(20);
        tree.insert(40);
        tree.insert(70);
        tree.insert(60);
        tree.insert(80);

        System.out.println("중위 순회 결과:");
        tree.inOrder();

        int keyToSearch = 40;
        Node searchResult = tree.search(keyToSearch);
        if (searchResult != null) {
            System.out.println("\n검색 결과: " + keyToSearch + " 찾음");
        } else {
            System.out.println("\n검색 결과: " + keyToSearch + " 찾지 못함");
        }

        int keyToDelete = 30;
        tree.delete(keyToDelete);
        System.out.println("\n노드 " + keyToDelete + " 삭제 후 중위 순회 결과:");
        tree.inOrder();
    }
}