자료구조 / Tree

---

Tree 란?

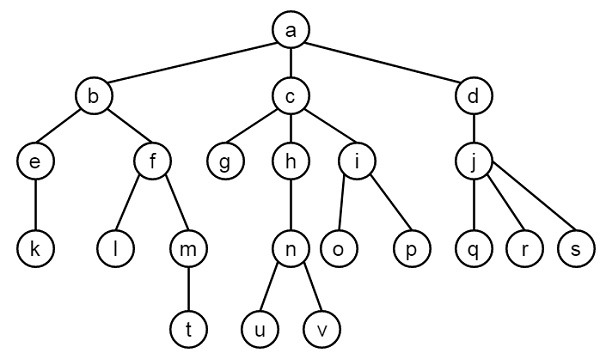
트리란 노드와 링크로 구성된 그래프의 일종이며 Cycle을 가지지 않는 자료구조이다. 계층적 구조를 나타낼 때 사용되기 때문에 폴더구조, 조직도, 가계도와 유사한 모습을 보인다.

---

Tree의 구조

• 노드(Node) : 트리 구조의 자료 값을 담고 있는 단위
• 에지(Edge) : 노드 간의 연결선 (=link, branch)
• 루트 노드(Root) : 부모가 없는 노드, 가장 위의 노드
• 잎 노드(Leaf) : 자식이 없는 노드
• 내부 노드(Internal) : 잎새 노드를 제외한 모든 노드
• 부모(Parent) : 연결된 두 노드 중 상위의 노드
• 자식(Child) : 연결된 두 노드 중 하위의 노드
• 형제(Sibling) : 같은 부모를 가지는 노드
• 깊이(Depth) : 루트에서 어떤 노드까지의 간선의 수
• 레벨(Level) : 트리의 특정 깊이를 가지는 노드 집합
• 높이(Height) : 트리에서 가장 큰 레벨 값
• 크기(Size) : 자신을 포함한 자식 노드의 개수
• 차수(Degree) : 각 노드가 지닌 가지의 수
• 트리의 차수 : 트리의 최대 차수

---

Tree의 특징

• 하나의 노드에서 다른 노드로 이동하는 경로는 유일
• 노드가 $N$개인 트리의 Edge의 수는 $N-1$개
• Acyclic (Cycle이 존재하지 않음)
• 모든 노드는 서로 연결되어 있음
• 하나의 Edge를 끊으면 2개의 Sub-Tree로 분리됨

---

Binary-Tree 란?

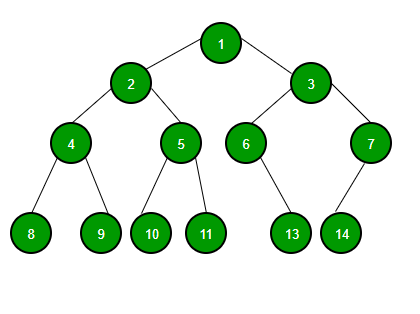
이진 트리는 각각의 노드가 최대 두 개의 자식 노드를 가지는 트리 자료 구조로, 자식 노드를 각각 왼쪽 자식 노드와 오른쪽 자식 노드라고 한다.

---

Binary-Tree의 특징

• 포화 이진 트리의 높이가 h일 때, 노드의 수는 $2*2^h - 1$
• 포화, 완전 이진 트리의 노드가 $N$개 일 때, 높이는 $logN$
• 이진 트리의 노드가 $N$개 일 때, 최대 가능 높이는 $N - 1$

---

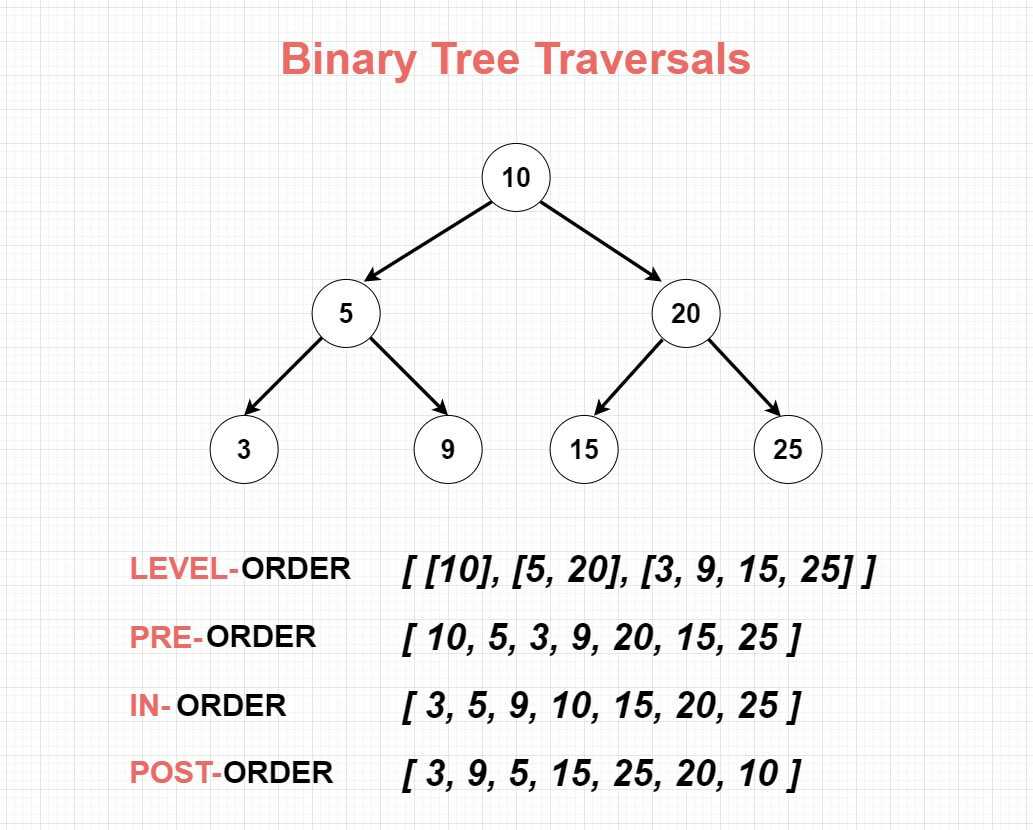
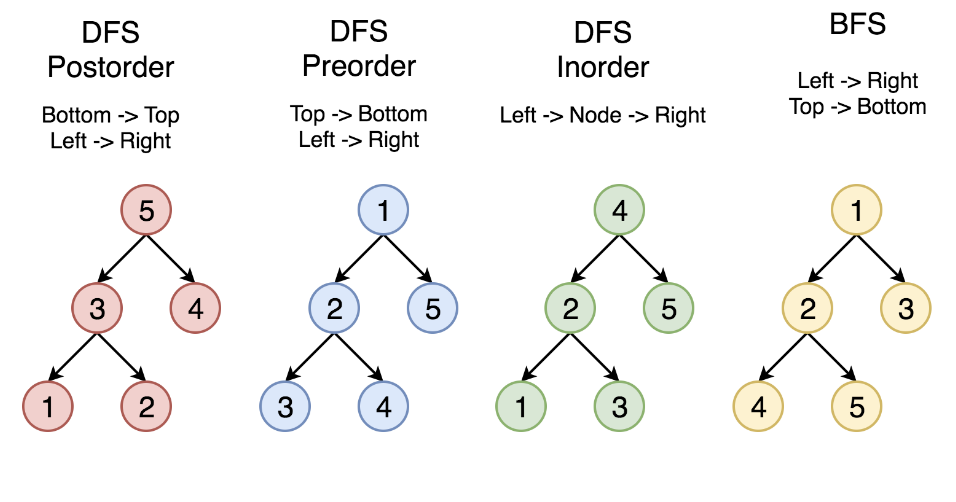
Binary-Tree Traversal

모든 노드를 빠뜨리거나 중복하지 않고 방문하는 연산

• 순회 종류는 총 4가지
  - Preorder : 전위 순회, DFS 중 하나
  - Inorder : 중위 순회, DFS 중 하나
  - Postorder : 후위 순회, DFS 중 하나
  - Levelorder : 레벨 순회, BFS
  

---

Binary-Tree 구현

• 배열로 구현

class TreeNode {
    int data;
    TreeNode left, right;

    public TreeNode(int item) {
        data = item;
        left = right = null;
    }
}

class BinaryTreeArray {
    TreeNode[] nodes;
    int maxSize;
    int size;

    public BinaryTreeArray(int maxSize) {
        this.maxSize = maxSize;
        this.size = 0;
        nodes = new TreeNode[maxSize];
    }

    public void insert(int data) {
        if (size < maxSize) {
            nodes[size++] = new TreeNode(data);
        } else {
            System.out.println("Tree is full, cannot insert more nodes.");
        }
    }

    public void preorderTraversal() {
        System.out.print("Preorder Traversal: ");
        preorderTraversalRec(0);
        System.out.println();
    }

    private void preorderTraversalRec(int index) {
        if (index < size && nodes[index] != null) {
            System.out.print(nodes[index].data + " ");
            preorderTraversalRec(2 * index + 1);
            preorderTraversalRec(2 * index + 2);
        }
    }

    public void inorderTraversal() {
        System.out.print("Inorder Traversal: ");
        inorderTraversalRec(0);
        System.out.println();
    }

    private void inorderTraversalRec(int index) {
        if (index < size && nodes[index] != null) {
            inorderTraversalRec(2 * index + 1);
            System.out.print(nodes[index].data + " ");
            inorderTraversalRec(2 * index + 2);
        }
    }

    public void postorderTraversal() {
        System.out.print("Postorder Traversal: ");
        postorderTraversalRec(0);
        System.out.println();
    }

    private void postorderTraversalRec(int index) {
        if (index < size && nodes[index] != null) {
            postorderTraversalRec(2 * index + 1);
            postorderTraversalRec(2 * index + 2);
            System.out.print(nodes[index].data + " ");
        }
    }

    public void levelOrderTraversal() {
        System.out.print("Level Order Traversal: ");
        for (int i = 0; i < size; i++) {
            if (nodes[i] != null) {
                System.out.print(nodes[i].data + " ");
            }
        }
        System.out.println();
    }
}

public class Main {
    public static void main(String[] args) {
        BinaryTreeArray treeArray = new BinaryTreeArray(10);

        treeArray.insert(1);
        treeArray.insert(2);
        treeArray.insert(3);

        treeArray.preorderTraversal();
        treeArray.inorderTraversal();
        treeArray.postorderTraversal();
        treeArray.levelOrderTraversal();
    }
}

• 연결 리스트로 구현

class TreeNode {
    int data;
    TreeNode left, right;

    public TreeNode(int item) {
        data = item;
        left = right = null;
    }
}

class BinaryTreeLinkedList {
    TreeNode root;

    public BinaryTreeLinkedList() {
        root = null;
    }

    public void insert(int data) {
        root = insertRec(root, data);
    }

    private TreeNode insertRec(TreeNode root, int data) {
        if (root == null) {
            root = new TreeNode(data);
            return root;
        }

        if (data < root.data) {
            root.left = insertRec(root.left, data);
        } else if (data > root.data) {
            root.right = insertRec(root.right, data);
        }

        return root;
    }

    public void preorderTraversal() {
        System.out.print("Preorder Traversal: ");
        preorderTraversalRec(root);
        System.out.println();
    }

    private void preorderTraversalRec(TreeNode node) {
        if (node != null) {
            System.out.print(node.data + " ");
            preorderTraversalRec(node.left);
            preorderTraversalRec(node.right);
        }
    }

    public void inorderTraversal() {
        System.out.print("Inorder Traversal: ");
        inorderTraversalRec(root);
        System.out.println();
    }

    private void inorderTraversalRec(TreeNode node) {
        if (node != null) {
            inorderTraversalRec(node.left);
            System.out.print(node.data + " ");
            inorderTraversalRec(node.right);
        }
    }

    public void postorderTraversal() {
        System.out.print("Postorder Traversal: ");
        postorderTraversalRec(root);
        System.out.println();
    }

    private void postorderTraversalRec(TreeNode node) {
        if (node != null) {
            postorderTraversalRec(node.left);
            postorderTraversalRec(node.right);
            System.out.print(node.data + " ");
        }
    }

    public void levelOrderTraversal() {
        System.out.print("Level Order Traversal: ");
        int height = height(root);
        for (int i = 1; i <= height; i++) {
            printGivenLevel(root, i);
        }
        System.out.println();
    }

    private int height(TreeNode root) {
        if (root == null) {
            return 0;
        } else {
            int leftHeight = height(root.left);
            int rightHeight = height(root.right);
            return Math.max(leftHeight, rightHeight) + 1;
        }
    }

    private void printGivenLevel(TreeNode root, int level) {
        if (root == null) {
            return;
        }
        if (level == 1) {
            System.out.print(root.data + " ");
        } else if (level > 1) {
            printGivenLevel(root.left, level - 1);
            printGivenLevel(root.right, level - 1);
        }
    }
}

public class Main {
    public static void main(String[] args) {
        BinaryTreeLinkedList treeLinkedList = new BinaryTreeLinkedList();

        treeLinkedList.insert(1);
        treeLinkedList.insert(2);
        treeLinkedList.insert(3);

        treeLinkedList.preorderTraversal();
        treeLinkedList.inorderTraversal();
        treeLinkedList.postorderTraversal();
        treeLinkedList.levelOrderTraversal();
    }
}