학습배경
최근 알고리즘 문제를 풀어보며 느낀점은, 알고리즘에 대한 지식이 완전히 체화되지 않았다는 느낌을 받았습니다. 주변 사람들이 쉽다는 문제를 정말 오랜시간이 걸려서 겨우 풀었기때문에, 이 느낌을 강하게 받았습니다 😓 이번 기회에 탐색 알고리즘에 대하여 확실히 정리하고 오랫동안 기억해보고자 합니다. 풀이했던 문제를 저만의 새로운 문제로 창작해보며, 만든 문제를 기반으로 개념을 쉽게 풀어쓰며 설명하도록 하겠습니다. 이 포스트가 깊이 있는 내용을 다루지는 못하지만, 탐색 알고리즘은 학습하는 분들에게도 도움이 되기를 바랍니다.
새롭게 만들어본 문제

현 문제는 백준 온라인 저지의 1697번 : 숨바꼭질 를 풀이하고, 저만의 새로운 아이디어로 만든 문제입니다. (해당 문제를 꼭 먼저 읽어보셨으면 해요!) 숨바꼭질 문제를 보면 대략 감을 잡았겠지만, 이 문제는 자동차가 주유소를 찾아서 주유하기 위해 최소 얼만큼의 시간동안 이동해야하는가를 구해야하는 문제입니다. 이때 각 턴마다 이동할 수 있는 왼쪽, 오른쪽 이동값이 주어짐을 가정했습니다. 즉, 예를들어 왼쪽 이동값 = 3, 오른쪽 이동 값 = 1 이라고 했을때, 위 예제의 경우 11, 8, 5, 6 순으로 이동하며 3시간동안 이동하게 됩니다.
문제의 질문 핵심, 접근방식

제가 만들어본 문제의 질문 핵심은, "최소" 몇번의 이동으로 주유소에 도달 가능한가입니다. 이를 위해선, 다음과 같은 방법을 생각해볼 수 있을 것 같아요. (1) 각 좌표에 대해 자동차가 이동할 때 마다 방문여부(이력) 을 남겨야합니다. 그래야 이전에 방문했던 칸을 중복하지 방문하지 않기 떄문입니다. 그리고 (2) 현 좌표칸에서 다음 좌표 칸으로 이동할 때 마다 이동 가능한 모든 좌표는 이동거리(버튼 횟수) 가 1씩 증가해야한다 라는 방법들로 문제 해결방법을 고안해볼 수 있을 것 같아요.
이 방법으로, 저는 플러드 필(Flood Fill) 이라는 알고리즘으로 해결할 수 있겠는데? 라는 생각으로 문제를 접근해봤습니다.
Flood Fill (플러드 필)
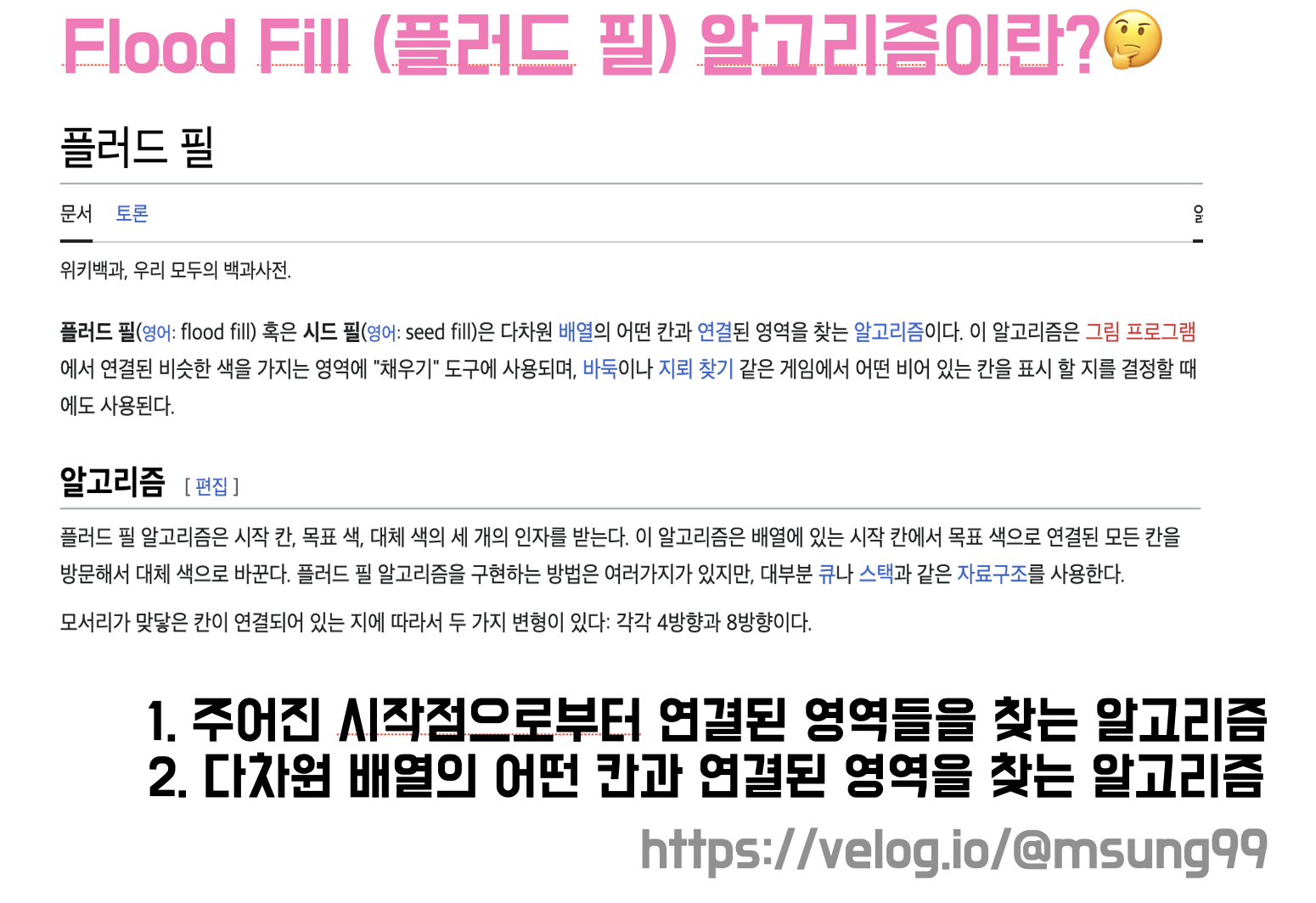
위키백과에 정의되어 있기를, 플러드 필(또는 시드 필) 이란 다차원 배열의 어떤 칸과 연결된 영역을 찾는 알고리즘입니다. 플러드 필 알고리즘은 시작 칸, 목표 색, 대체 색 3가지의 인자를 받는다고 하네요 🤔
이 외에도 많은 자료에서 정의하길, 주어진 시작점으로부터 연결된 영역을 찾는 알고리즘이라고 합니다. 또는 다차원 배열으 어떤 칸과 연결된 영역을 찾는 알고리즘입니다.

플러드 필의 가장 대표적인 예시로는 "그림 색칠하기" 가 많이 거론되는 것으로 보입니다. 인접합(또는 직접 관련된) 영역을 차례때로 칸을 색칠해나가는 방식이죠. 이때 색칠해가면서, 색칠이 불가능한 영역은 대상에서 제외합니다. 또한 이미 색칠한 영역은 중복해서 또 다시 색칠하지 않는다는 특징이 있습니다.

이러한 플러드 필의 특징을 보아하니, 저는 이 문제를 해결할 때 이 알고리즘을 적용하면 아주 좋겠는데? 라는 생각을 해보게 되었어요. 우선 앞서 살펴봤던 위키백과의 정의문을 다시 가져와봤는데, 정의문을 다시 비교해봅시다. 우선 (1)배열을 사용하며, (2) 현재 칸과 직접 이어지는(직접 관련된) 영역을 찾는다는데 유사 특징이 있습니다. 또 (3) 인접한 모든 칸을 방문 표시하며, (4) 탐색을 시작할 좌표, 목표 좌표, 다음에 탐색할 좌표를 입력받는데 매우 유사한 특징을 지닙니다.
BFS vs DFS
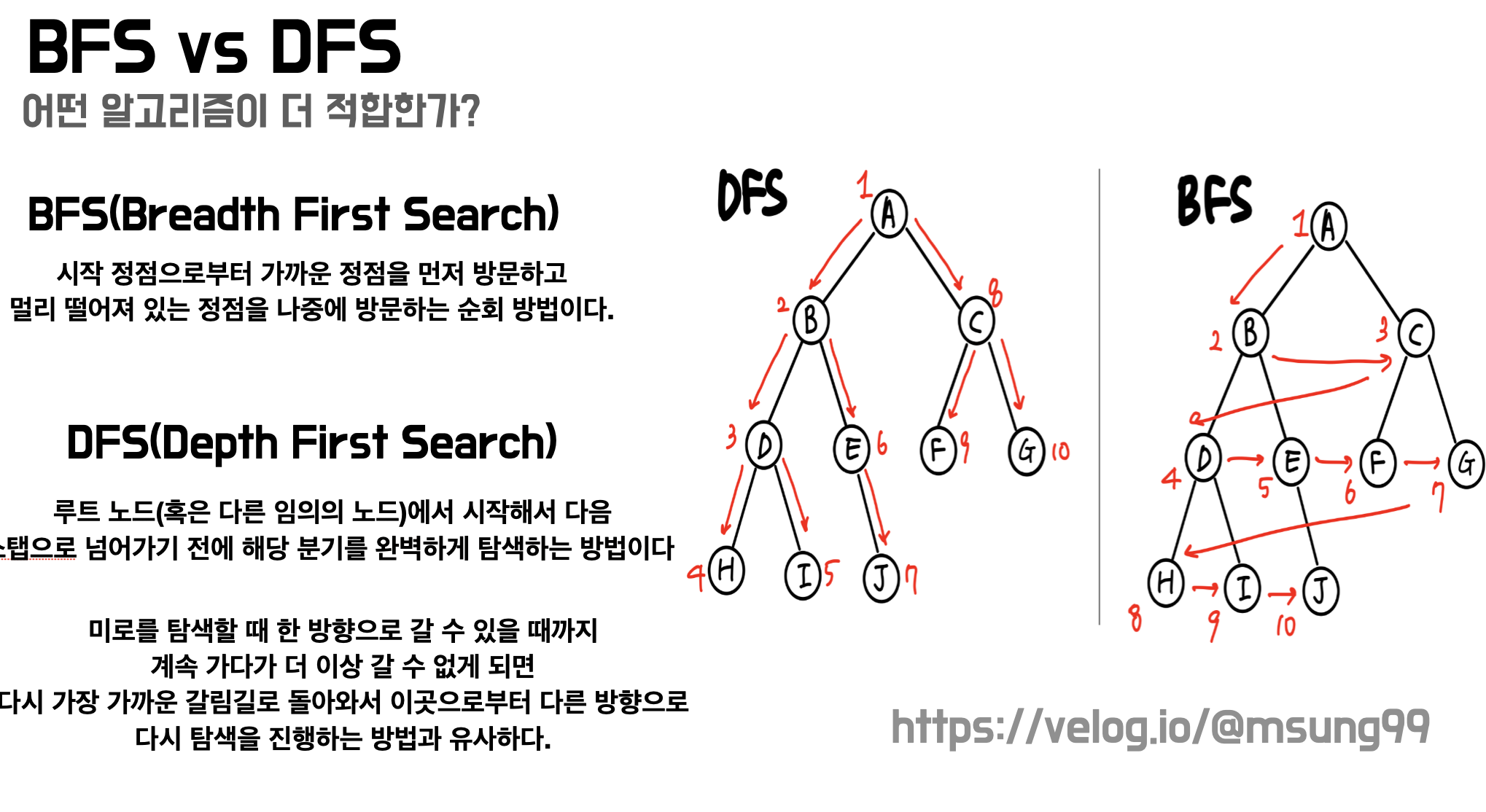
그런데 사실 플러드 필은 다소 추상적인 개념이에요. 이 알고리즘을 실제로 구현할 수 있는 알고리즘 기법으로는 BFS(Breadth First Search), DFS(Depth First Search) 가 있습니다. 그렇다면 둘 중 어떤 알고리즘 기법이 더 효율적일까요? 🧐 결론부터 말하자면, 저는 BFS 를 선택했습니다.
DFS 를 활용하는 경우
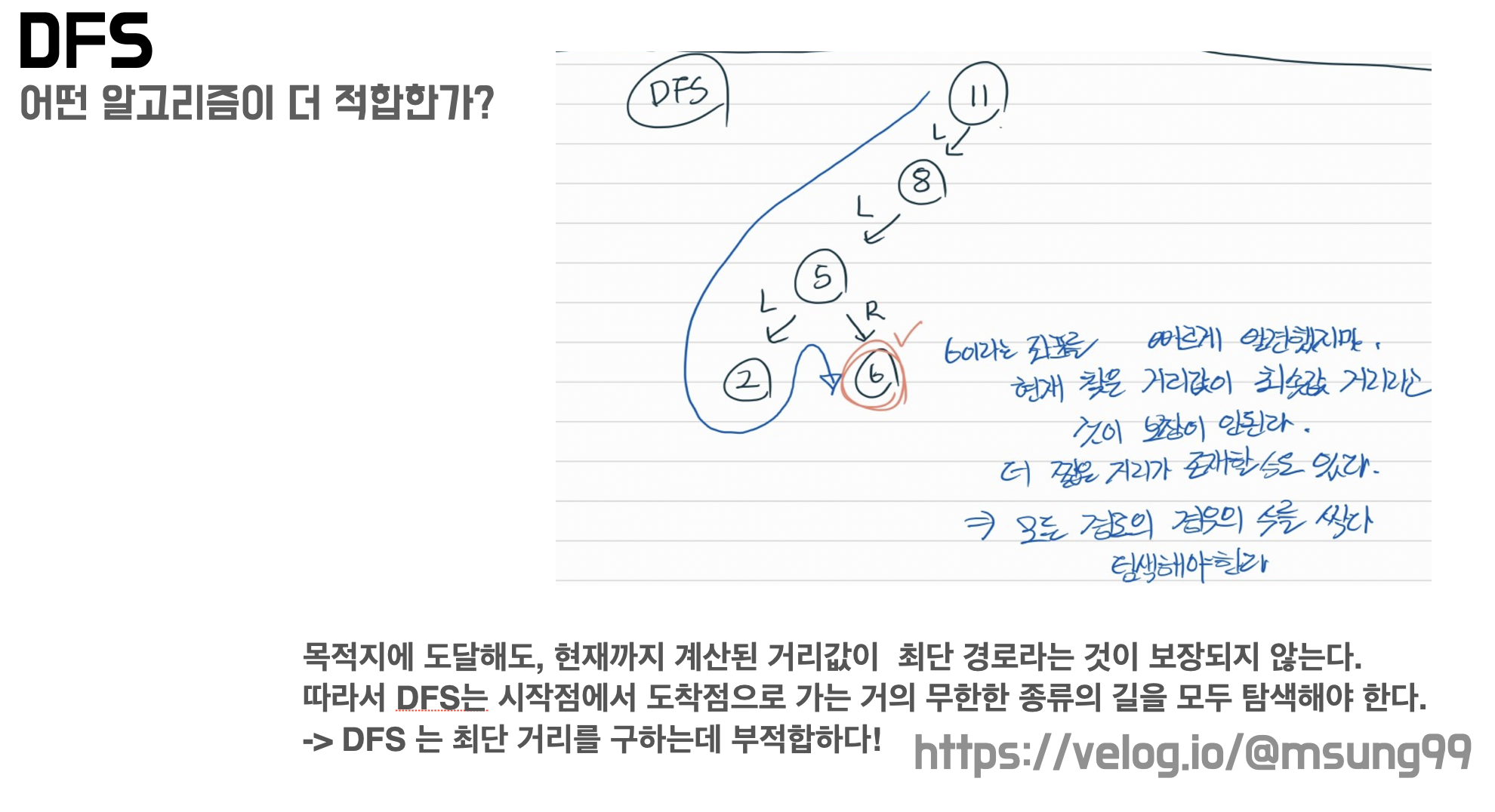
만약 DFS 를 활용한다면, 매우 비효율적인 탐색을 시도할 수 있습니다. 예를들어 좌표 11에서 6으로 자동차가 이동하는 경우를 가정해보죠. 그렇다면 DFS 의 특성상 깊이를 우선적으로 탐색하기 때문에, 목적지에는 운이 좋다면 매우 빠른 속도로 접근이 가능해요. 하지만, 목적지에 도달해도 현재까지 계싼된 거리값이 최단 거리 값이라는 것이 보장되지 않습니다. 따라서 DFS 를 활용한다면, 시작점에서 도착점으로 가는 모든 경로의 경우를 싹다 탐색해야합니다.
BFS 를 활용하는 경우
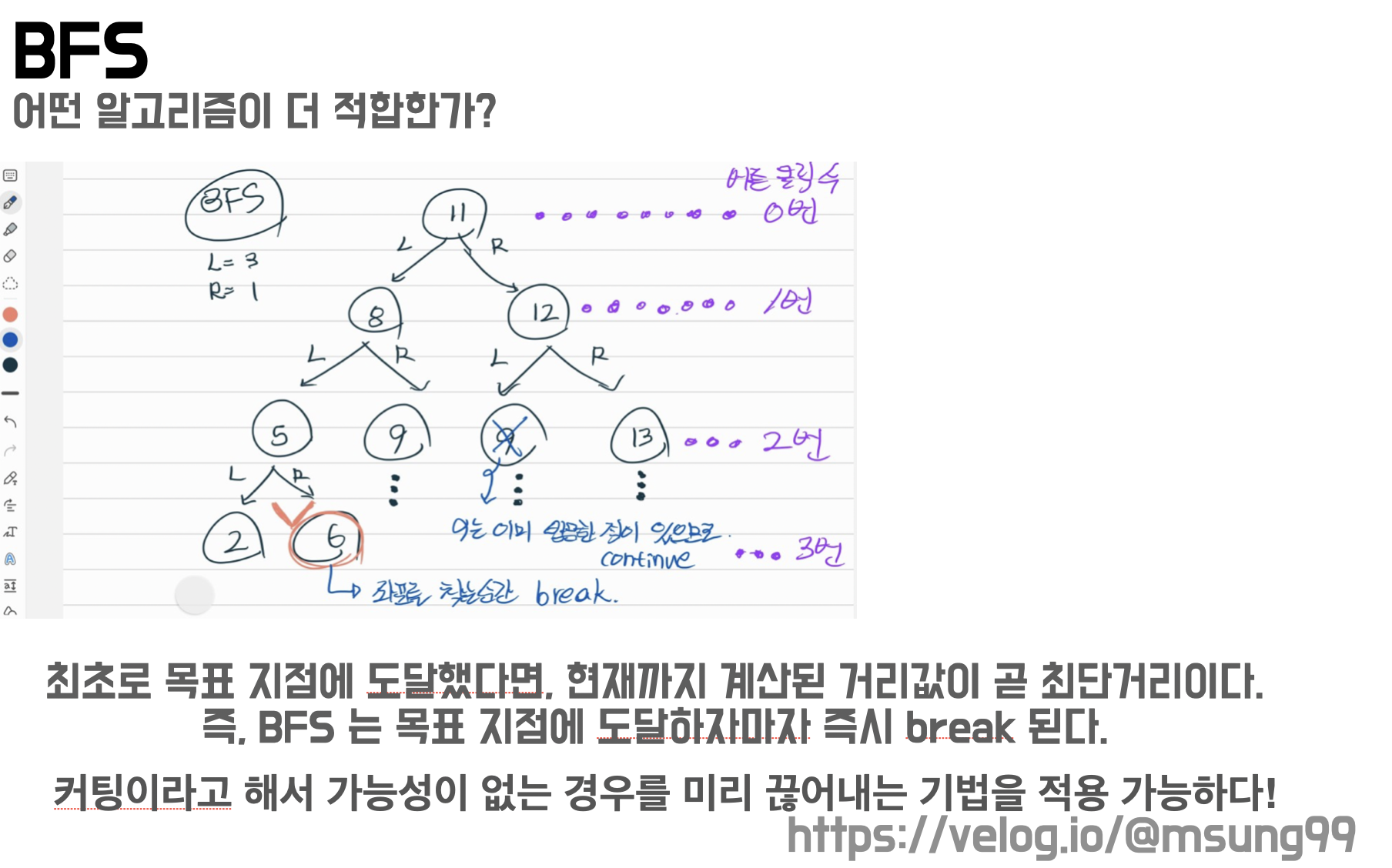
반면 BFS 를 활용한다면, 커팅 기법 을 적용함으로써 탐색이 불필요한 경로에 대해선 더 이상 진행하지 않을 수 있습니다. 최초로 목표로 지점에 도달했다면, 현재까지 계산된 거리값이 곧 최단거리입니다. BFS 를 활용하면 목표 지점에 도달하자마자 즉시 탐색 반복문을 종료시킬 수 있게됩니다.
구현코드
구현 코드는 아래와 같습니다. c++ 을 기준으로 작성해봤어요!
#include <iostream>
#include <queue>
#include <algorithm>
using namespace std;
bool visited[1000001];
int n, start, target, left, right;
int bfs(){
bool check = false;
queue<pair<int, int>> q;
q.push(make_pair(y, 0));
visited[start] = true;
while(!q.empty()){
int cur = q.front().first();
int cnt = q.front().second();
q.pop();
visited[cur] = true;
if(cur == x){
return cnt;
}
if(cur + ri <= n && !visited[cur + ri]){
visited[cur + ri] = true;
q.push(make_pair(cur + ri, cnt + 1));
}
if(cur - le >= 0 && !visited[cur - le]){
visited[cur - le] = true;
q.push(make_pair(cur - le, cnt + 1));
}
}
return -1;
}
int main(void){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
fill(visited, visited + n, true);
cin >> n >> target >> start >> left >> right;
visited[start] = true;
cout << bfs();
}각 좌표 칸마다 방문 여부를 체크하기 위한 1차원 배열 visited 를 선언해줬습니다. 또 fill() 로 visited 배열을 모두 false 로 초기화후 BFS 를 수행하게 됩니다.
알고리즘의 플로우는 다음과 같이 구성해봤습니다. 우선 (1) 시작하는 칸을 큐에 넣고 방문했다는 표시를 남깁니다. 다음으로 큐에서 원소를 꺼내며 그 칸에 좌우로 이동할 칸에 대해 이런 과정들을 진행합니다.(2-1) 해당 칸을 처음 방문했다면 방문했다는 표시를 남기고 해당 칸을 큐에 삽입합니다.(2-2) 반대로 이전에 방문한 칸이라면 아무것도 수행하지 않습니다. 그러고 (3) 표적을 찾았다면 탐색을 충단하고 거리 값을 반환합니다. (4) 이 과정들을 큐가 빌 때까지 반복합니다. 이때, 큐가 완전히 빌 때까지도 While 문이 끝난게 아니라면 주유소를 찾지 못한것입니다.
동적 게획법(DP) 로는 해결하지 못할까? 🤔
이번 문제를 풀이해보면서 강력하게 느낌을 받았던것은, BFS 탐색 알고리즘 외에도 다이나믹 프로그래밍(DP) 기법, 즉 동적 계획법을 활용하여 문제를 해결할 수 있지 않을까라는 생각도 들었습니다. 아직 DP 에 대한 온전한 이해를 하지못했다는 생각이 들었기 때문에, 이 문제에 대한 DP 활용 풀이법이 생각난다면 추후 포스트에서 다루어보고자 합니다. 우선 지금 단계에선 DP 알고리즘이 무엇인지에 대해서 간략히 개념만 짚고, 왜 DP 설계 방법을 생각해보게 되었는지를 간략히 정리해보고자 합니다.
동적 계획법이란?
DP, 흔히 동적 계획법이라고도 불리는 알고리즘은 최적화 이론의 한 기술입니다. 특정 범위까지의 값을 구하기위해, 그것과 다른 범위까지의 값을 활용하여 효율적으로 값을 구하는 알고리즘 기법입니다.
최종적인 답을 구하기 위해, 기존의 문제를 작은 단위(Sub-Problem) 으로 분할하고, 분할한 문제를 또 최대한 작은 단위로 분할한 후 조금씩 작은 문제를 해결하며 궁극적으로 기존의 큰 문제를 해결하는 방식입니다. 이때 메모이제이션(memoization) 이라는 방식을 활용하는데, 이전에 계산했던 결과값을 어딘가에 저장해두었다가 큰 문제를 해결할 때 기존 계산 결과값을 재활용하는 방식입니다. 이때 "어딘가" 란 배열, 벡터등의 자료구조가 대표적인 예가 될것입니다.
답을 구하기 위해서 했던 계산을 또 하고 또 하고 계속해야 하는 종류의 문제의 구조를 최적 부분 구조(Optimal Substructure) 라고 부릅니다. 동적 계획법은 이런 문제에서 효과를 발휘합니다.
그래서 왜 DP ?
지금부터 설명하는것은 신뢰성 없는 근거와 생각이 대부분이므로, 참고용으로 읽어도 좋을듯합니다. 우선 문제의 조건은 위에서 언급했듯이, 입력값 N 의 최댓값이 1백만입니다. 이러한 입력값은 알고리즘 문제 해결 전략 에 따르면, 대략 "O(n)" 시간에 해결되어야 함을 추정해볼 수 있습니다.
DP 는 이 시간복잡도를 만족하기에 아주 적합한 알고리즘입니다. DP 는 1차원 배열의 형태를 메모이제이션 기법을 적용했을때 보통의 문제라면 O(n) 에 해결되는 경우가 많습니다. 또한, 앞서 설명했듯이 중복되는 계산 을 피하기위해 BFS 알고리즘으로 문제를 해결했었습니다. 이 "중복 방지" 라는 특징은 DP 알고리즘의 전형적인 특징이자 활용 이유이기도 합니다.
하지만 이에 대한 해결법은 아직 명확한 근거가 없습니다. 따라서 DP 로 해결 가능한지에 대한 추가적인 학습과 고민이 필요합니다.
마치며
이렇게 새로운 문제를 한번 풀이해봤는데, 이 풀이가 효율적인 방법일진 모르겠네요! 하지만 탐색 알고리즘을 정말 오랜만에 풀이해보면서, 알고리즘에 대한 지식을 견고하게 정리해볼 수 있었던 것 같습니다 🙂
더 학습해볼 키워드
- 다이나믹 프로그래밍 (흐... 알고리즘 유형은 너무 많고 어렵네요 🥲)
