Counting Sort, Radix Sort, STL Sort

msung99·2022년 7월 3일
알고리즘
0
post-thumbnail

위와 같은 리스트를 정렬하기 위해선 앞서 살핀 버블, merge, 퀵 정렬모두 사용 가능하다.

하지만 퀵정렬은 O(nlogn) 이 보장되지 않는다.
퀵정렬은 최악의 경우 O(n^2) 이 걸린다!

Counting Sort

  • 각 숫자가 몇번 등장했는지를 카운팅해서 배열 arr 에 저장해 놓고,
    나중에 for 문으로 arr 을 순회하면서 각 숫자가 등장한 횟수만큼 해당 숫자를 출력하는 방식

  • 숫자의 범위가 0 ~ 999999999 과 같이 너무 범위가 큰 경우는 크기가 1억인 배열을 생성해야 하므로, 메모리 제한 문제가 발생!

=> 숫자의 범위가 1천만 이하일때만 counting sort 를 쓰자!

시간 복잡도 : O(n+k)

  • 수의 범위가 k개라고 하떄 맨 처음 n개의 수를 보면서 arr 배열에 값을 추가하고 답을 출력할때, 혹은 정렬을 수행할때 총 k칸의 값을 확인해야 하므로 O(n+k) 이다.

  • 즉, 수의 범위 k가 작을때는 counting sort 가 굉장히 효율적으로 동작함!

수의 범위가 작을때는 (1천만 이하일때) 카운팅 소트를 사용하면 구현이 아주 간단하게 활용하기 좋다!
But 수의 범위가 너무 크면 메모리 제한에 걸릴수있으므로 사용하지 말것!

Radix Sort

일의자리, 십의자리, 백의자리, ... 순으로 정렬을 수행하는 알고리즘

  • 자릿수를 이용해서 정렬을 수행하는 알고리즘
  • 카운팅 소트를 응용한 알고리즘

예시

아래와 같은 리스트를 정렬하는 방법을 생각해보자.

과정1 : 일의 자리를 기준으로 리스트를 정렬하기

  1. 원소의 개수만큼의 크기를 가진 배열을 생성한다.
    즉, 크기가 10인 배열을 생성한다.

  2. 생성한 배열에다 숫자를 1의 자리에 따라서 배열에 넣는다.

  • 즉, 012 는 일의 자리가 2이므로 인덱스 2에 넣고, 421은 일의 자리가 1이므로 인덱스 1에 넣는다.

아래는 각 배열에 들어가는 수를 적은 것이다.

  1. 배열에서 0번 인덱스부터 차례대로 꺼내면서 출력하면 1의자리를 기준으로 정렬되는 상태가 될 것이다.

이떄 421과 021을 보면, 421이 원본 리스트에서 021 보다 앞에 있어서 일이 자리 수가 같은 1임에도 불구하고 재배열 과정을 마치면 421이 자연스래 더 앞으로 오게된다.

=> Radix sort 의 결과, 일의 자리 순으로 정렬이 완료되었으며, 일의 자리가 같은 수들 끼리는 맨 처음의 순서가 유지된다 ( = 원본 리스트에 앞에 있던 원소가 재배열 후에도 더 앞에 위치하게 된다 )

과정2 : 일의 자리를 기준으로 정렬된 리스트를, 십의 자리를 기준으로 또 정렬하기

위에서 일의 자리를 기준으로 정렬된 리스트를,
이번엔 십의 자리를 기준으로 삼아서 정렬을 시키면 아래와 같다.

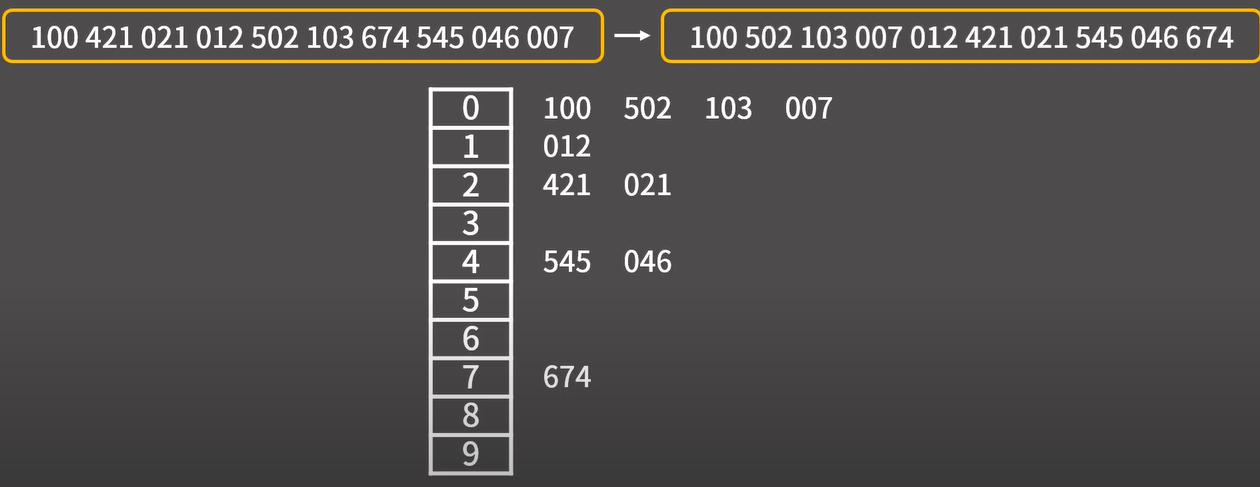
과정3 : 십의 자리를 기준으로 정렬된 리스트를, 백의 자리를 기준으로 정렬하기

정렬 결과는 아래와 같다.

Radix Sort 원리

두 수 A,B의 위치 관계를 생각해보면 A > B 일때 더 큰 자리에서 A의 자릿수가 B의 자릿수보다 큰 경우가 먼저 생기므로, Radix sort에서 결국 언젠가는 B가 A보다 앞에 올 수 밖에 없으므로,
그 상대적인 위치가 게속 유지된 채로 정렬 과정이 끝난다.

왜 이러한 정렬방법이 통하는 것인지 그 원리를 생각해보자.

두 숫자를 대소비교를 하는 것은 가장 큰 자릿수(백의 자리) 부터 차례대로 비교해 간다.

백의 자리가 동일하다면 그 뒤로는 십의 자리, 또 십의 자리가 동일하다면 일의 자리 순으로 비교를 진행해 나간다.

상세분석

정렬이 다 끝났을때, 421 은 502 보다 리스트의 앞 인덱스에 위치해야 할 것이다.

비록 십의 자리를 비교할때까지는 502가 421 앞에 위치했지만,
그 전까지의 둘의 위치가 어디에 있는지와 전혀 무관하게

백의 자리에 대해 재배열을 할때 421은 4번 리스트에 들어가는 반면,
502는 5번 리스트에 들어가기 때문에 재배열을 끝낸 후
421이 502보다 앞에 올 수 밖에 없다는걸 알 수 있다.

Radix sort 의 시간복잡도 : O(D*n)

  • 자릿수의 개수가 D개라고 할때, D번에 걸쳐서 카운팅 소트를 하는것과 동일하다.

그러면 리스트의 개수를 k개라고 할때, 엄밀하게 말하면 시간복잡도는 O(D(n+k)) 이지만,
보통 리스트의 개수는 n에 비해 무시가 가능할 정도로 작다.

Radix sort 구현법 : vector 또는 링크드리스트로 구현

  • Radix sort 를 배열로 구현시 단점 : 공간 제약

  • Radix sort 를 수행하기 위해 10개의 리스트가 필요하다.

  • 실제 구현시 c++ 배열을 이용하면 n개의 원소를 정렬할때, 한 리스트에 n개의 원소가 다 몰릴수도 있으므로, 10개의 리스트를 모두 n칸의 배열로 만들어야해서 공간 낭비가 심함

Radix sort 구현

int n = 15;
int arr[1000001] = {...};.
int d = 3;
int p10[3];


int digitNum(int x, int a){
  return (x / p10[a])  % 10;
}

vector<int> l[10];

int main(void){
  p10[0] = 1;
  for(int i = 1; i < d; i++)
    p10[i] = p10[i-1] * 10;
  
  for(int i=0; i < d; i++){
    for(int j = 0; j < 10; j++)
      l[i].clear();
    for(int j = 0; j < n; j++)
      l[digitNum(arr[j], i).push_back(arr[j]);
    int adix = 0;
    for(int j=0; j < 10; j++)
      for(auto x : l[j])
        arr[aidx++] = x;
  }
}

for(int i=0; i < n; i++)
  cout << arr[i] << ' ';

STL sort

  • STL sort 는 퀵소트를 기반으로 하지만, 불균등하게 쪼개지는 상황이 계속 반복되어서 재귀의 깊이가 너무 깊어져도 O(nlogn) 이 보장되는 정렬 알고리즘이다.

  • 그래서 STL sort 는 최악의 경우에도 O(nlogn) 이므로 마음 편하게 쓰면 된다!

시간 복잡도에 대해 조금 더 설명해보면, sort 함수의 구현은 intro sort라는 정렬 방법을 바탕으로 했는데, 이 방법은 quick sort에 heap sort와 insertion sort를 섞은 방식으로 평균 nlogn, 최악의 경우 n^2의 시간 복잡도를 가지는 quick sort와는 달리, 최악의 경우에도 nlogn을 보장한다.

STL sort 에 비교함수(사용자 정의함수) 를 인자값으로 넣기

  • 사용자 정의 비교함수를 인자값으로 넣어줄 수 있다.

ex. 원소를 5로 나눈 나머지 값으로 우선 대소 비교하고, 5로 나눈 나머지가 같은 경우에는 크기 순으로 정렬하고 싶은 경우
=> 아래와 같이 비교 함수를 만들어서 인자로 넘겨주면 된다.

// a가 b의 앞에 와야할 때 true, 그렇지 않으면 false 를 리턴
bool compare(int a, int b){   
  if(a % 5 != b % 5)
    return a%5 < b%5;
  return a < b;
}

int arr[7] = {1,2,3,4,5,6,7}; 
sort(a, a+7, compare);   // 배열 arr 은 5-1-6-2-7-3-4 순으로 정렬된다.

비교함수 정의할시 주의사항

1. 비교함수는 두 값이 같을때 (혹은 우선순위가 같을때) 반드시 false 를 리턴해야한다!

예시
아래 함수는 얼핏보면 문제가 없어보이지만, a와 b가 같을 경우에 true 를 리턴하므로 에러가 발생한다.
=> sort 함수가 도는 과정에서 런타임 에러가 발생할 수 있음!

( 비교함수가 올바르지 않다고 해도 100% 런타임 에러가 발생하는 것은 아니여서 두 값이 같을때 true 를 리턴해도 운이 좋으면 통과가 될수도 있긴하다. 하지만 가급적이면, 아니 무조건 런타임 에러가 발생하는 것을 막기위해 같을 경우에는 false 를 리턴하도록 비교 함수를 구현하자! )

bool cmp(int a, int b){
  if(a > b)
    return true;
  return false;
}

아래가 올바른 예시이다.

bool compare(int a, int b){
  return a > b;
}

2. 비교함수의 인자 값으로 STL 혻은 클래스 객체를 전달시 레퍼런스를 사용하는 것이 좋다!

  • 문자열을 받아서 끝자리의 알파벳으로 정렬하고 싶은경우 비교함수를 아래와 같이 해도 되겠지만, 비효율적이다.
bool compare(string a, string b){
  return a.back() < b.back();
}

함수의 인자로 STL 이나 구조체 객체를 실어서 보내면 값의 복사가 일어나는데,
지금 이 비교함수를 생각해보면 굳이 복사라는 불필요한 연산을 추가로 하면서 불필요한 시간을 잡아먹을 필요가 없다!

따라서 복사를 하는 대신에, 레퍼런스를 사용하는 것이 더 바람직하다.

// 아래와 같이 const 를 사용하는 경우, a와 b의 값은 변하지 않는다는 것을 명시적으로 나타내는 것이므로, 
// 값이 변하지 않는 다는 것을 명시적으로 표현하고 싶다면 const 키워드를 붙이는 것도
// 좋은 방법이다! (몰론 필수사항은 아님)
bool compare(const string& a, const strring& b){
  return a.back() < b.back();
}

stable_sort( )

  • 다만 STL sort는 stable sort 가 아님. 따라서 동일한 우선순위를 가진 원소를 사이의 상대적인 순서가 보존되지 않을 수 있다.

  • 꼭 stable sort 정렬방법이 필요한 경우 stable_sort() 함수를 사용하면 된다!

  • pair, tuple 등을 먼저 가장앞의 원소를 대소비교하고, 값이 같다면 그 다음 원소를 비교하는 방식

profile
msung99
https://haon.blog
이전 포스트

선택정렬, 버블정렬, 병합정렬, 퀵정렬

다음 포스트

다이나믹 프로그래밍(DP)

0개의 댓글