삽입, 선택, 버블정렬
- 모두 O(n^2)
- 면접에서 대부분 이 3가지 정렬방식을 물어볼 일 거의없음!!
- 삽입, 선택, 버블정렬을 굳이 외우지 말고, 버블 정렬정도는 구현할 수 있을 정도만 학습하자.
선택정렬(Selection Sort) : O(n^2)
-
O(n^2)
-
max_element(arr, arr+k) 함수 : arr[0], arr[1], arr[2], ..., arr[k] 중에서 최댓값인 원소의 주소값을 반환하는 함수
int arr[10] = {3, 2, 7, 116, 62, 235, 1, 23, 55, 77};
int n = 10;
for(int i = n-1; i > 0; i--){
swap(*max_element(arr, arr+i+1), arr[i]);
}버블정렬(Bobble Sort) : O(n^2)
-
앞에서부터 인접한 두 원소를 보며, 앞의 원소가 뒤의 원소보다 클 경우 자리를 바꾸는 작업을 반복
-
결과적으로, 가장 큰 값부터 맨 뒤 인덱스에 차례대로 쌓이게 되서 오름차순 정렬이 된다.
=> 인접한 원소를 비교하며 자리바꿈하는 한 턴이 지났을때, 적어도 맨 뒤에는 최댓값이 위치해있게 된다.
- 비교횟수 : n-1 번 + n-2 번 + ... + 3번 + 2번 + 1번 = n(n-1)/2
구현코드
int arr[5] = {-2, 2, 4, 6, 13};
int n = 5;
for(int i = 0; i < n; i++){
for(int j=0; j < n-1-j; j++){
if(arr[j] > arr[j+1])
swap(arr[j], arr[j+1]);
}
}예시
과정1

과정2
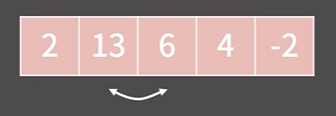
과정3
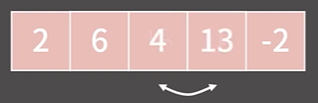
과정4

결과

이렇게 한턴이 끝나면 적어도 맨 마지막 인덱스에 최댓값이 위치해 있게 된다.
최종결과

병합정렬(Merge Sort) : O(nlogn)
- 재귀적으로 수열을 나눠 정렬한 후 합치는 정렬방법
- 크기가 n, m 인 두 정렬된 리스트를 합쳐서 크기 n+m 의 정렬된 리스트를 만든다.
종류1. 정렬된 두 리스트를 병합하는 방법 : O(n+m)
-
두 정렬된 리스트의 맨 앞 원소를 비교해서, 둘 중에 더 큰 값을 리스트에서 추출해내고 새로운 리스트 (크기가 n+m) 인 리스트에 삽입한다.
-
두 리스트가 모두 빌때까지, 즉 크기가 n+m인 새롭게 병합된 리스트가 완성될때까지 계속 두 리스트 맨앞의 값을 비교하고 추출한 다음 새로운 리스트에 삽입하는 과정을 반복한다.
예시

종류2. 정렬되지 않는 두 리스트를 병합하는 방법 : O(nlogn)
- 재귀를 활용할것.
과정
- 정렬하고자 하는 주어진 리스트를 2개로 쪼갠다.
- 나눈 리스트 2개를 각각 정렬한다.
- 정렬된 두 리스트를 합친다.
예시

시간복잡도 분석
병합정렬의 과정은 크게 2가지로 나눌 수 있다.
1. 리스트를 분할하는 과정 : O(n) (= 2n-1)
2. 분할된 리스트를 다시 하나의 리스트로 병합하는 과정 : O(nlogn)
리스트의 크기 n = 2^k 이라고 하자.
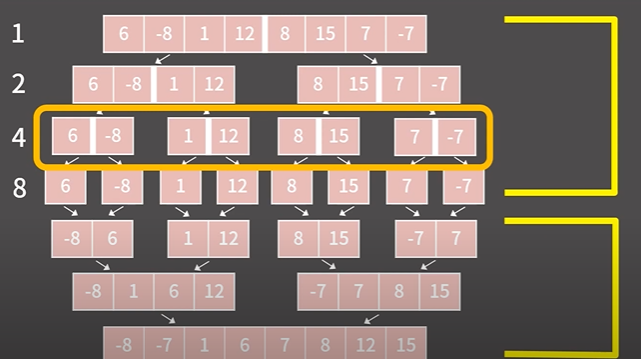
- 리스트를 분할하는 과정
우선 위 그림처럼 재귀호출시 3번째 줄처럼
리스트는 총 4개로 쪼개지고, 각각의 리스트에 대해 함수가 호출 될 것이므로 해당 줄에서 함수는 총 4번 호출될 것이다.
=> 분할하는 과정에서 총 함수호출 횟수 = 1 + 2 + ... + 2^k = 2n -1 = O(n)번 호출된다.
- 분할된 각 리스트를 다시 하나의 리스트로 병합하는 과정 : O(nlogn)
- 각 줄에서 두 리스트가 짝지어서 다음 단계(병합되기)로 넘어가기 위해선 전체 원소의 개수만큼 필요하다.
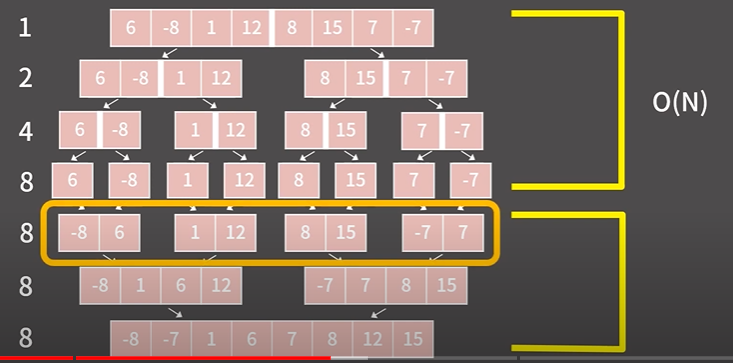
예를들어 위처럼 크기가 N/4 인 4개의 리스트가 둘씩 짝지어서 병합되려면
필요한 연산의 횟수는 N/4 + N/4 + N/4 + N/4 = N 이 된다.
그리고 분할이 완료됐을때 리스트의 원소는 1개였다가 2^k 개가 될때까지 매번 2배씩 커지니까 줄은 k개이다.
병합정렬 구현
#include <iostream>
#include <string>
#include <vector>
#include <algorithm>
using namespace std;
int arr[1000001];
int tmp[1000001]; // merge 함수에서 리스트 2개를 합친 결과를 임시로 저장하고 있을 변수
// arr의 인덱스 (st ~ mid) 와 인덱스 (mid ~ en-1) 에 이미 정렬되어 있을때,
// arr의 st ~ (en-1) 을 정렬하는 함수이다.
// => 즉, 2개의 정렬된 두 리스트 배열을 합치는 것을 구현하는 함수
void merge(int st, int en) {
int mid = (st + en) / 2;
int lidx = st; // arr[st:mid] 에서 값을 보기위해 사용하는 인덱스
int ridx = mid; // arr[mid:en] 에서 값을 보기위해 사용하는 인덱스
// 정렬된 두 배열 리스트의 원소를 하나씩 차곡차곡 값을 비교하며 새로운 리스트로써 병합시킴
for (int i = st; i < en; i++)
{
if (ridx == en) { // 2번쨰 리스트의 원소를 끝까지 다 써버린 경우
tmp[i] = arr[lidx];
lidx++;
}
else if (lidx == mid) { // 1번쨰 리스트의 원소를 끝까지 다 써버린 경우
tmp[i] = arr[ridx];
ridx++;
}
else if (arr[lidx] <= arr[ridx]) { // 2번쨰 리스트의 원소값이 더 큰 경우
tmp[i] = arr[lidx];
lidx++;
}
else { // 1번쨰 리스트의 원소값이 더 큰 경우
tmp[i] = arr[ridx];
ridx++;
}
}
for (int i = st; i < en; i++) {
arr[i] = tmp[i]; // tmp 에 임시저장해둔 값을 arr 로 다시 옮김
}
}
// 배열 arr의 인덱스 st ~ (en-1) 을 정렬하는 함수
void merge_sort(int st, int en) {
if (st + 1 == en) // base condition : 배열의 크기가 1일때
return;
int mid = (st + en) / 2;
merge_sort(st, mid); // 주어진 리스트 배열 arr 을 2개로 쪼개고 각각 정렬한다.
merge_sort(mid, en);
merge(st, en); // 2개로 나눈 두 리스트를 정렬시키면서 병합한다.
}
int main(void)
{
ios::sync_with_stdio(0);
cin.tie(0);
int n;
cin >> n;
for (int i = 0; i < n; i++)
cin >> arr[i];
merge_sort(0, n);
for (int i = 0; i < n; i++)
cout << arr[i] << '\n';
}Stable sort
-
우선순위가 같은 원소를끼리는 원래의 순서를 따라가도록 하는 정렬방법
-
우선순위가 같은 원소가 여러 개일때 다양한 경우로 정렬된 결과가 나올 수 있다.
-
첫번째로 무조건 정렬이 된다고 보장된 정렬방법
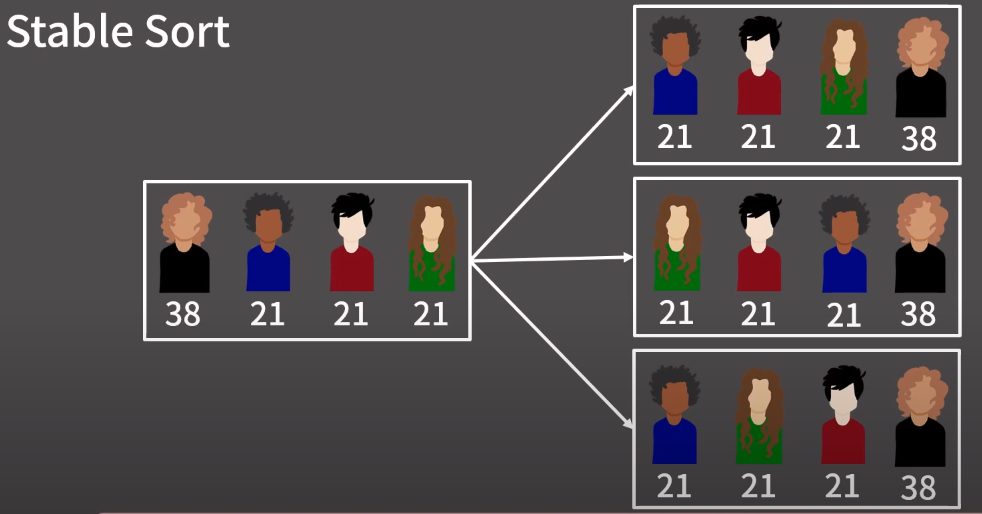
예를들어 위와 같이 나이가 38, 21, 21, 21 인 4명의 사람이 있을때 21,21,21은 우선순위가 동일하므로 다양한 정렬 결과가 나올 수 있다.
- merge sort 는 stable sort의 일종임.
- 위 성질을 만족시키려면, 앞서 본것처럼 앞 리스트에서 현재 보는 원소와 뒤 리스트에서 현재 보는 원소의 우선 순위가 같을 때 앞 리스트의 원소를 먼저 보내줘야한다.
stable sort 응용 사례
- 2차원 좌표 (x, y) 를 정렬하는 상황
=> 좌표들을 x가 작은순으로, x가 동일하다면 y가 작은 순으로 정렬하고 싶은 경우

1.먼저 y의 크기를 기준 삼아서 merge sort 를 수행하고
2.다음으로 x의 크기를 기준으로 x의 크기를 기준 삼아서 merge sort 를 수행할 수 있다.
=> 이렇게 하면 stable sort 의 성질 덕분에 일단 x가 작은게 앞으로 올거고,
x가 같다면 x에 대해 정렬을 수행하기 전에 앞에 있었을 원소,
즉 y가 작은 원소가 앞에 오게 될 것이다.
=> 사실 이렇게 merge sort 를 2번 수행하면 비효율적이니 1번만 수행하기 위해,
정렬된 두 배열을 합치는 merge 함수에서 a[aidx] 와 b[bidx] 를 비교하는 부분만 살짝 바꿔주면 된다.
Unable sort
- 첫번째로 무조건 정렬이 된다고 보장할 수 없고 2번째나 3번쨰로 정렬이 될 수도있는 정렬방법
퀵 정렬(Quick Sort)
-
매 단계마다 pivot 원소를 제자리로 보내는 작업을 반복한다.
-
병합정렬처럼, 재귀적으로 구현되는 정렬방법
-
pivot 원소는 원소중에 아무거나 잡아도 됌.
다만 pivot으로 설정된 원소는 맨 앞 인덱스에 위치해야한다.
- pivot 의 올바른 위치를 설정하는 규칙
=> pivot의 왼쪽에는 pivot 보다 작은 원소들이,
pivot의 오른쪽에는 pivot 보다 큰 원소들이 위치하게 한다.
정렬방법
아래처럼 pivot 을 임의로 6을 설정했을때,
6보다 작은 원소들은 6의 왼쪽에 위치하게 되며,
6보다 큰 원소들은 6의 오른쪽에 위치하게 된다.
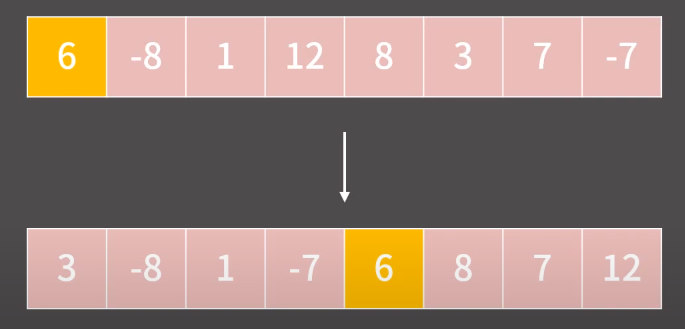
pivot 기준으로 왼쪽 리스트와 오른쪽 리스트를 각각 따로따로 정렬한다.
과정1) 임시배열 tmp를 만들고 pivot을 제외한 나머지 원소들을 제외하면서
먼저 pivot 이하인 값들을 다 tmp 에 넣는다.
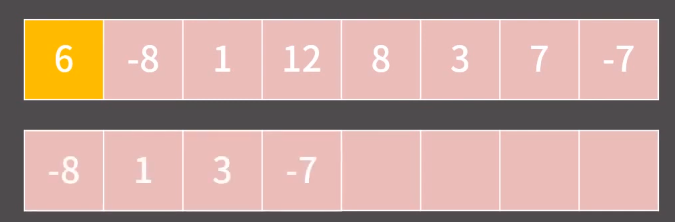
과정2) pivot 이하의 값들을 tmp 에 다 넣었다면, pivot 을 tmp 에 넣는다.
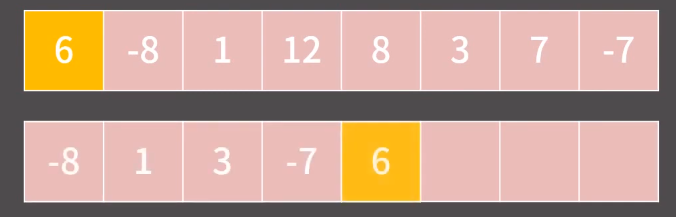
과정3) 다시한번 pivot 을 순회하면서 pivot 초과인 값들을 tmp에 넣는다.

과정4) 마지막으로 tmp를 원래 배열에 덮어쓰면 끝이다.
퀵정렬 구현 1 - 안좋은 구현방법!!!
- 아래처럼 구현하는 경우 O(n) 이 걸리지만,
퀵 정렬의 장점인 "추가적인 공간" 을 필요하지 않는다는 성질을 무너뜨리게 된다.
int arr[8] = {7, -8, 12, 8, 3, 7, -7};
int tmp[8];
int tidx = 9;
int pivot = arr[0]; // pivot 은 맨 앞의 원소로 설정
for(int i = 1; i < 8; i++)
if(arr[i] <= pivot) // pivot 보다 작은 원소들에 대해
tmp[tidx++] = arr[i]; // tmp 배열에다 추가
tmp[tidx++] = pivot; // pivot 보다 작은 원소들을 다 넣었다면, pivot 도 tmp 에 추가
for(int i = 1; i < 8; i++)
if(arr[i] > pivot) // pivot 보다 큰 원소들에 대해
tmp[tidx++] = arr[i]; // tmp 배열에다 추가
for(int i = 0; i < 8; i++)
arr[i] = tmp[i]; // tmp 배열로 정렬한 원소들을 다시 기존 배열 arr 에 옮김 퀵정렬 구현 2 - in-place sort
- 추가적인 공간을 사용x
- 방법 : 양쪽끝에 포인터 2개를 두고 두개의 원소를 적절하게 스왑하면 된다.
원리
- 핵심
l 은 pivot 보다 큰 값이 나올떄까지 오른쪽으로 이동한다.
r 은 pivot 보다 작은 값이 나올때까지 작거나 같을 값이 나올떄까지 왼쪽으로 이동한다.
아래처럼 포인터 l 과 r 을 두었다고 하자.
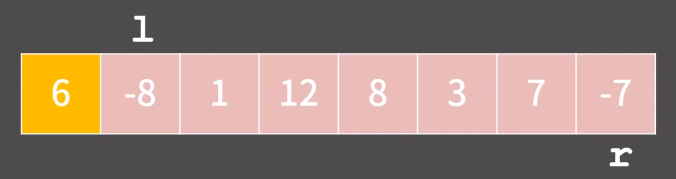
먼저 l 을 pivot 보다 큰 값이 나올때까지 오른쪽으로 이동하면 12에서 멈추게 된다.
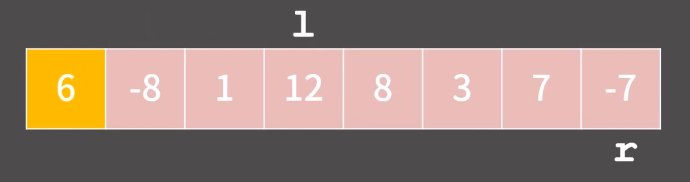
그 다음으로 아래처럼 r 을 pivot 보다 작거나 같은 값이 나올때까지
왼쪽으로 이동시킨다.
그런데 애초에 지금 -7이 pivot 보다 작으니 이동할 필요 없다!
그러나, 지금 pivot 보다 큰 12가 왼쪽에 있고 pivot 보다 작은 -7이 정작 오른쪽에 있는게 말이 안된다.
따라서 l 과 r 의 둘의 자리를 바꾼다!
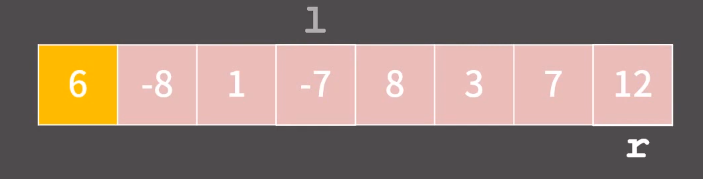
그리고 또 다시 l을 계속 움직이면 8에서 멈추고, r은 3에서 멈춘다.
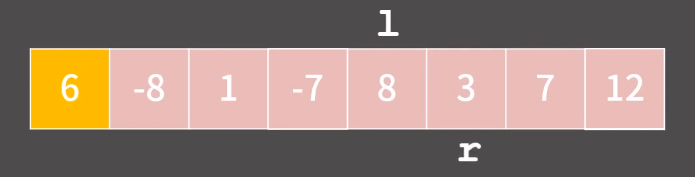
그렇다면 이번에도 l 과 r 의 둘의 자리를 바꾼다!
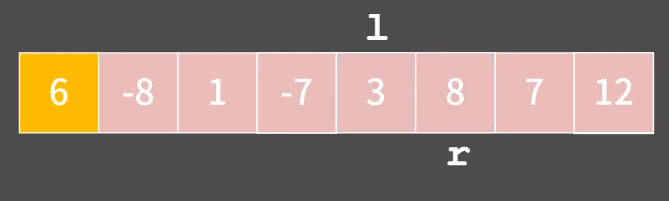
다시 l 을 옮기다보면 8에서 멈추고, r은 옮기다가 l 보다 왼쪽에 위치한 그 즉시 멈춘다!
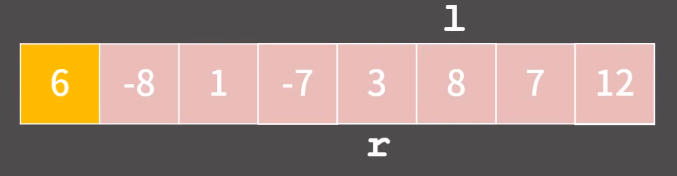
이렇게 r 이 l 보다 작아진 순간이 오면 pivot 과 r 을 스왑하면서 알고리즘이 종료된다!
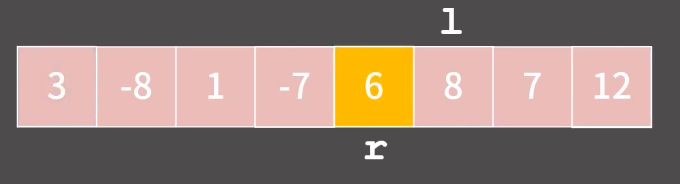
=> 모든 순간에 l 의 왼쪽에는 pivot 보다 작거나 같은 원소들만 있고,
r의 오른쪽에는 pivot 보다 큰 원소들만 있다는 점에 주목하면 된다.
in-place 퀵정렬 구현
- 상수 번의 연산으로 l 과 r 이 가까워지기 떄문에 O(n) 이다.
간단구현
int arr[8] = {7, -8, 12, 8, 3, 7, -7};
int pivot = arr[0]; // pivot 은 맨 앞의 원소로 설정
int l =1, r = 7;
while(1){
while(l <= r && arr[l] <= pivot) // pivot 과 비교하며 l 을 계속 1 증가시키다가 while 문을 벗어나게 되면
l++; // l 이 가리키는 곳이 가리키는 곳이 바로 pivot 보다 큰 값이 된다.
while(l <= r && arr[r] > pivot) / pivot 과 비교하며 r 을 계속 1 감소시키다가 while 문을 벗어나게 되면
r--; // r 이 가리키는 곳이 가리키는 곳이 바로 pivot 보다 큰 값이 된다
if(l > r)
break;
swap(arr[l], arr[r]);
}
swap(arr[0], arr[r]);재귀적으로 구현
int n = 10;
int arr[1000001] = {...};
void quick_sort(int st, int en){
if(en <= st + 1) // base condition : 현재 보는 리스트 구간의 길이가 1이하인 경우
return;
int pivot = arr[st];
int l = st + 1;
int r = en - 1;
while(1){
while(l <= r && arr[l] <= pivot)
l++;
while(l <= r && arr[r] >= pivot)
r--;
if(l > r)
break;
swap(arr[l], arr[r]);
}
swap(arr[st], arr[r]);
quick_sort(st, r);
quick_sort(r+l, en);
}
int main(void){
quick_sort(0, n);
for(int i = 0; i < n; i++)
cout << arr[i] << ' ' ;
}퀵 정렬 in-place 구현의 시간복잡도 : O(n)
pivot 을 기준으로 양쪽 두개의 리스트로 나뉜다.
양쪽에서 따로 pivot 을 제자리로 보내는 과정을 반복하면 된다.
- pivot 을 제자리로 보내는 과정 : 해당 리스트의 크기에 비례
=> 각 단계마다 O(n) 이 소요
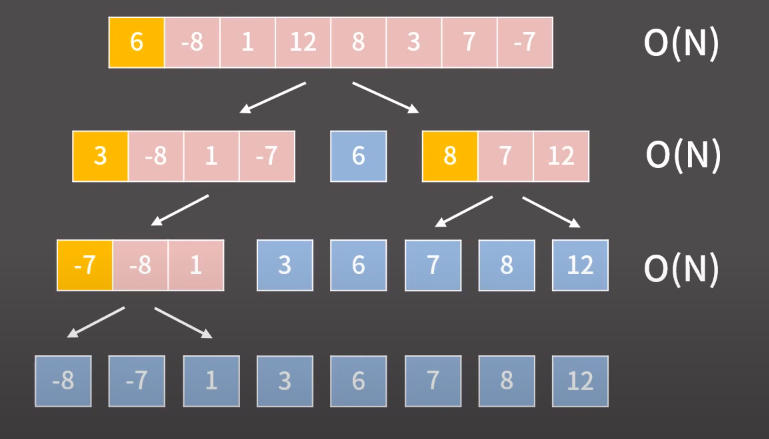
첫번째 줄은 O(n) 인 것은 자명하고, 두번째 줄은 각 리스트는 4에 비례하고 3에 비례하므로 합치면 대략 n에 비례한다.
=> 이런 식으로 각 단계에서 pivot 을 제자리로 보내야한는 리스트의 길이의 합은 n 이여서 각 단계마다 O(n) 이므로 필요하다.
- Average case : pivot 이 매번 완벽하게 중앙에 위치해서 리스트를 균등하게 쪼갠다면 단계의 개수는 merge sort 떄와 같이 O(log n) 이 될 것이다.
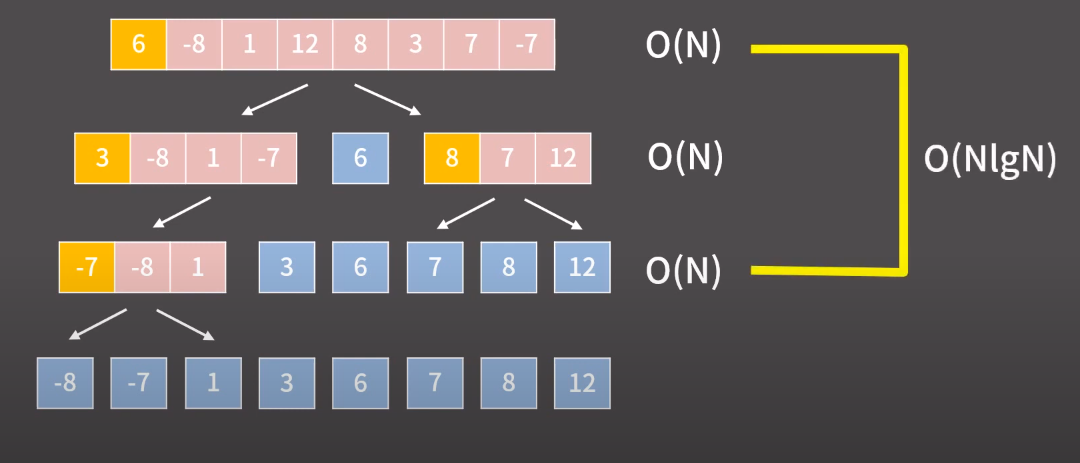
퀵정렬의 한계 (Worst case)
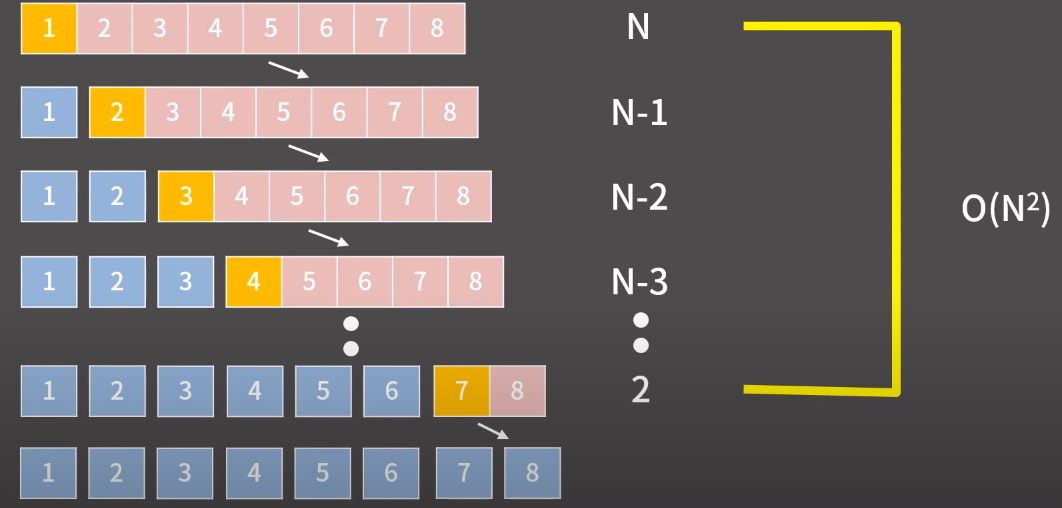
- Worst case : O(n^2) 아래 그림과 같은 경우
-
1,2,3,4,5,6,7,8 과 같은 경우
-
매번 선택되는 pivot 은 중앙에 가는대신 매번 가장 맨앞(왼쪽)에 위치하게 되고, 그로 인해 단계는 log n 개가 아닌 n 개가 된다.
=> 시간복잡도를 계산하면 O(n^2) 이 된다.
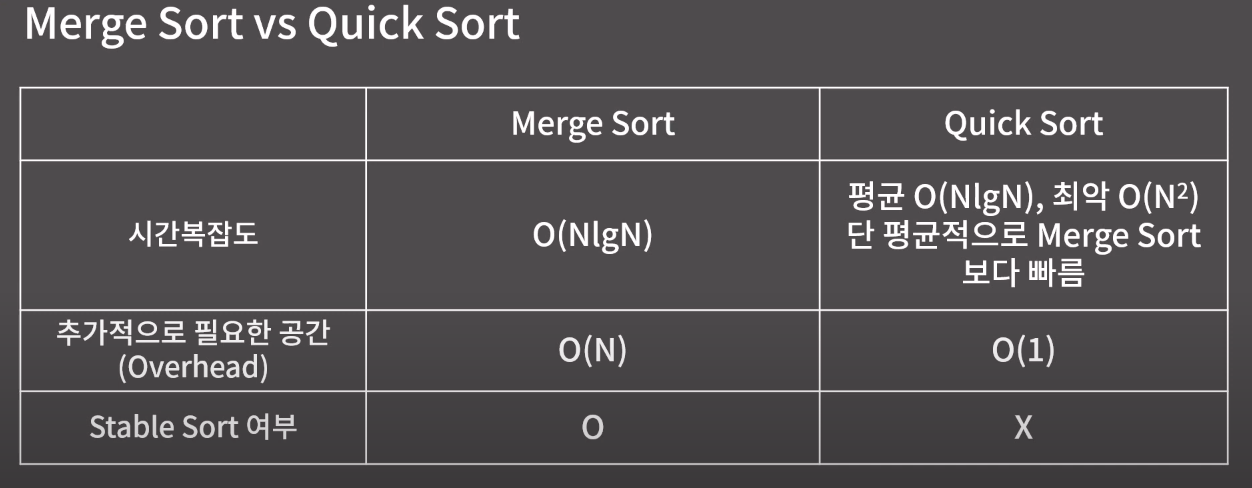
정리 : Merge sort VS Quick Sort