운영체제 : 메모리 계층 구조와 캐싱

본 포스트는 학교 수업 강의내용을 단순 정리본 형태로 만든 내용입니다. 평소 포스트와 달리 다소 설명이 부실할 수 있음을 미리 알려드립니다 🙂
Memory

메모리는 프로그램을 실행하기 위한 작업공간으로써 필요하다. 메모리에는 프로그램의 명령어들과 데이터들이 저장되어있고, 그게 실행됨에따라 변화한다.
메모리 성능개선을 위한 요소들
컴퓨터에 메모리를 적용하기 위한(성능 개선을 위한) 요구사항들은 어떤것들이 있을까?
=> 1) capacity (용량) / 2) cost (비용) / 3) access time (속도)
메모리의 용량이 크고, 가격이 싸고, 속도가 빠르면 좋을것이다.
그리고 메모리의 물리적인 용량에 커짐에 따라 OS 도 상호적으로 계속 역사적으로 진화한다.
이 메모리라는 것은 Processor (처리기) 가 프로그램을 처리할때 기본적으로 한 명령어를 처리할때 메모리 접근이 필요하다. 접근해서 fetch 해오고 필요에 따라서는 Load 해온다. 즉, 메모리 접근은 여러번 일어날 수 있음을 인지하자! 메모리 위에서 프로그램의 성능이 제약될 수 있는 아키텍처가 있다.
이에따라, Processor 하고 메모리는 이왕이면 시간이 흘러감에따라 상호작용적으로 같이 진화하는게 성능 측면에서 좋을것이다.
메모리 계층(Memory Hierarchy) 의 등장
아직 시장에 저 3개 요소들을 모두 완벽히 만족시키는 메모리는 존재하지 않는다. 예를들어 SRAM, DRAM 을 보자. SRAM 은 빠르지만 비싸다는 단점이 있고, DRAM 은 싸지만 느리다는 단점이 있다.
아직 완벽한 메모리는 등장하지 못했다. 따라서 완벽한 메모리가 없어서 컴퓨터 시스템은 하나의 특정 메모리 구성요소로만 구성할 수 없고, multiple 한 다양한 종류의 메모리 구성요소로 진화하게 되었다. 그리고 그 다양한 메모리 종류 구성요소들이 메모리 계층(Memory Hierarchy) 를 이루게 되었다.
Memory Hierarchy
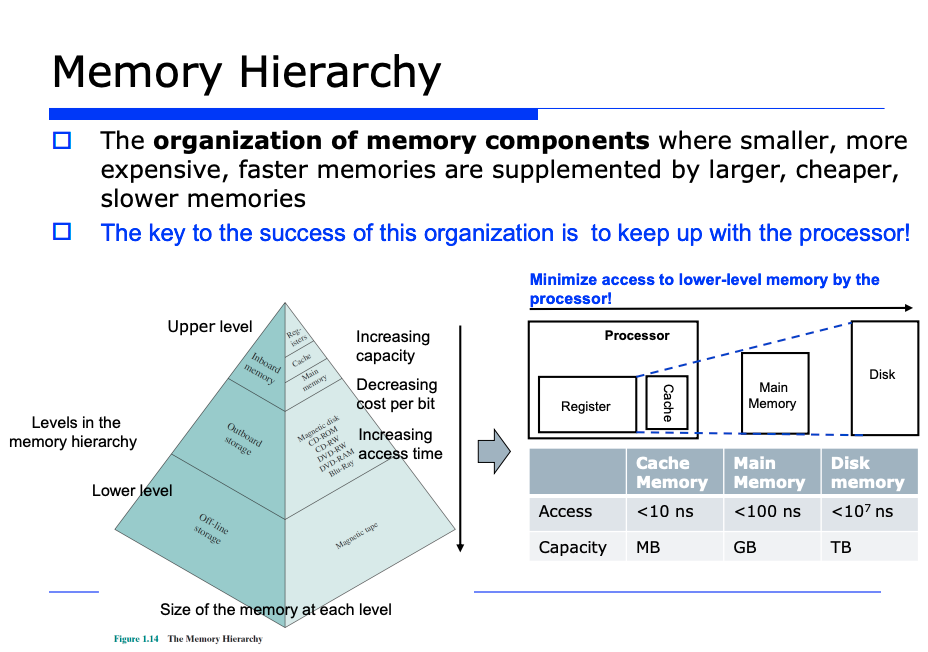
CPU 근처에는 더 빠른 메모리들을 배치시키는 방식으로 진화했다.
앞서 말했듯이 프로세서(처리기) 와 메모리는 밸런스있게 속도에 있어서 균형을 맞추어주는 것이 좋다. 따라서 프로세서 근처 (즉 CPU 근처) 에는 빠른 메모리들을 배치시키고, 점차 멀어질수록 느린 종류의 메모리들을 배치시키는 방식으로 진화되었다.
또 데이터 접근에 있어서 메모리 계층에서 하위 레벨에 있는 메모리들에 대한 접근 빈도(access frequency) 를 낮추고, 반대로 상위 레벨에 있는, 즉 속도가 빠른 메모리들에 대해서는 접근 빈도를 높이는 방식의 전략으로 진화했다.

자주 사용되는 데이터에대한 접근빈도를 높이기 위해서는, 당연히 그 프로그램에서 자주 쓰는 데이터들을 상위계층의 메모리들에다 저장하고, 자주 사용하지 않는 데이터들은 하위 계층의 메모리들에다 저장하자는 것이 전략이다.
locality
이런 전략들을 어떻게 구현할 것인지에 대한 연구를 진행했고, 가장 중요한 이론적인 근거가 바로 locality 라는 것이다. locality of reference 라는 것은 한국말로 "참조의 지역성", 즉 "참조의 집중화"로 번역이된다. 프로그램이 수행될때 어떤 일정한 시간동안 관찰해보면, 특정 메모리 계층만 참조하는 현상이 실제로 발견된다.
또 locality 는 2가지로 나뉜다. 시간적인 집중화(locality in time), 공간적인 집중화(locality in space) 이다.
-
locality in time (시간적인 집중화) : 한번 참조된 데이터는 조만간 곧 또 참조될 확률이 높다는 것
=> ex) 반복문의 경우, 같은 주소를 계속 참조하는 현상이 발생한다 -
locality in space (공간적인 집중화) : 배열을 생각하면 된다. 반복문을 순회하면서 배열 원소들을 조회할때 100, 104, 108번지, ... 순으로 조회한다. 즉 한번 참조하면 그 근처에 있는 메모리가 참조될 수 있는 확률이 높다는 것이다.

메모리를 구성할때 2가지의 메모리 구성요소가 있다고 가정해보자.
-
Hit : Hit 라는 것은 어떤 access 한 데이터가 있을때, 상위계층의(즉, 더 빠른) 메모리 구성요소에서 데이터가 발견되는 것을 의미한다.
- T1 : 상위계층(빠른) 메모리에 대한 access time 을 의미
- T2 : 하위계층(느린) 메모리에 대한 access time 을 의미
-
Miss : 상위 계층에는 없고, 하위 계층에서 발견되는 데이터를 의미한다. (상위계층에 없으니까 miss 된 것이다)
예제

- Level1 즉, 1번째 상위계층에 대한 access time (T1) 을 0.1uS 라고 가정하자.
- Level2 즉, 2번째 상위계층에 대한 access time (T2) 을 1uS 라고 가정하자. 다시말해서 T1 보다 10배 느린것이다.
- 그리고 hit rate 은 0.95, 즉 95 % 라고 가정하자.
hit rate 이 95 % 라고 가정했으므로 miss rate 은 5 % , 즉 0.05 가 된다.
이에 따라 총 access time 인 T 를 계산해보자.
어떤 데이터가 주어졌을때 먼저 상위계층에 Processor 가 갈것이다. 가서 hit 가 될 확률이 0.95 인것이고, 접근했을때 시간인 T1 은 0.1uS 이다.
반면 실패했을때는 캐시를 봤더니 miss 가 된것으로 확인하고 하위레벨에 접근할떄의 access time 인 T2 가 1uS 인것이다.
이런것을 감안하고 계산해보면 총 access time 인T = 0.15uS 가 나오는것이다. 이게바로 average access time 인것이다.
지금보듯이 결과값 0.15uS 를 보면 평균 access 시간이 T1 에 근사한다.

그리고 앞선 예제에서 T1 과 T2 를 10배가 차이나도록 예시를 보였다. 그런데 실무에서는 T1 과 T2 의 차이가 10배가 아닌 100배, 1000배가 될 수도있다.
hit rate 이 95% 와 97% 일때가 과연 차이가 있을까라는 생각이 들수있다. 겉보기에는 access time 이 99% 와 97% 가 얼마 차이 안날것같지만, 때에 따라서는 그렇지 않을수도 있다. hit rate 으로 성능을 판단하는것은 꽤나 애매해진다.
예를들어 miss penalty 가 100사이클이 돌떄, 97% 가 hit 되었을때는 4사이클이 나오고, 99% 일때는 2사이클이 나오게된다. 이건 보듯이 2배가 차이난다. 이러한 이유로 hit rate 보다는 miss rate 를 가지고 성능 분석을 하는것이 좋다.
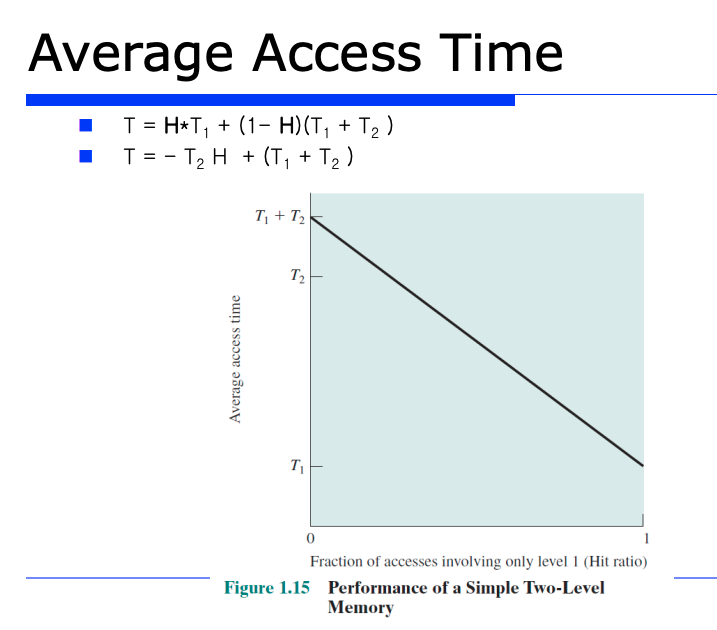
앞서 본 Average Access Time 을 수학적인 수식으로 표현해봤다.
- T = H * T1 + (1-H)(T1 + T2)
=> H : Hit rate, T1 : 상위계층에 대한 access time, 1-H : miss rate, T2 : 하위 계층에 대한 access time
hit rate 을 증가시킴에 따라 average access time 이 어떻게 변화하는지를 보려고하는 것이다. 그런데 앞서 공식 T = H * T1 + (1-H)(T1 + T2) 을 정리해보면, 아래와 같다.
- T = - T2 * H + (T1 + T2)
즉 기울기는 -T2 가 된다. H, 즉 Hit Rate 가 100% 일때를 생각해보면 위 공식에다 H = 1 을 대입해보면 T = T1 이 된다. 즉 Hit 가 싹다 되면 당연히 상위계층 메모리 (캐시) 에서 데이터가 싹다 리턴되는것이다. 즉 상위계층 메모리의 access time 이 바빠질것이다.
그런데 이것은 이론적인 것이고, 실무는 이런 이론적인 것과 완전히 동일할 수는 없을것이다. 근사값을 가지지 완벽히 동일하진 못한다.

하지만 이 그래프의 lower bound (하한선) 을 통해 상위계층에 대한 access time 인 T1 보다 average access time 이 더 좋아질수는 없다는것을 알 수 있다.
반대로 메모리에 대한 관리를 엄청 못해서 average access time 값이 완전 커도, 아무리 커도 T1 + T2 보다는 클 수 없다는 것을 알 수 있다.

앞선 설명들로 메모리 계층구조가 왜 필요하고, 어떻게 컴퓨터 메모리를 사용해야 효율적으로 성능 개선이 될지를 locality 를 통해 이해했다.
이를통해 실질적으로 캐시(Cache) 부터 시작해보자. 왜냐면 중심은 프로세스인데, 아까 말했듯이 프로그램을 실행하려면 명령어들마다 fetch 를 해와야한다. 즉 최소 1번 메모리에 접근해야한다. 그래서 성능이라는 것은 메모리에 속도에 종속될 수밖에 없는것이다. 메모리의 속도가 빠를수록 성능이 좋은것이다.
따라서 항상 프로세서(Processor) 와 메모리 속도의 밸런스를 유지하는것이 중요하다. 우리는 프로세서와 가까운 위치에 캐시를 배치할것이다. 이왕이면 자주 access 하는 메모리를 CPU 쪽에 가까이 배치하고, 자주 사용안하는 메모리를 멀리 배치하는 전략을 사용할텐데, 특히 Temporal locality 와 Spatial locality 를 어떻게 구현하는지를 지금부터 살펴보자!
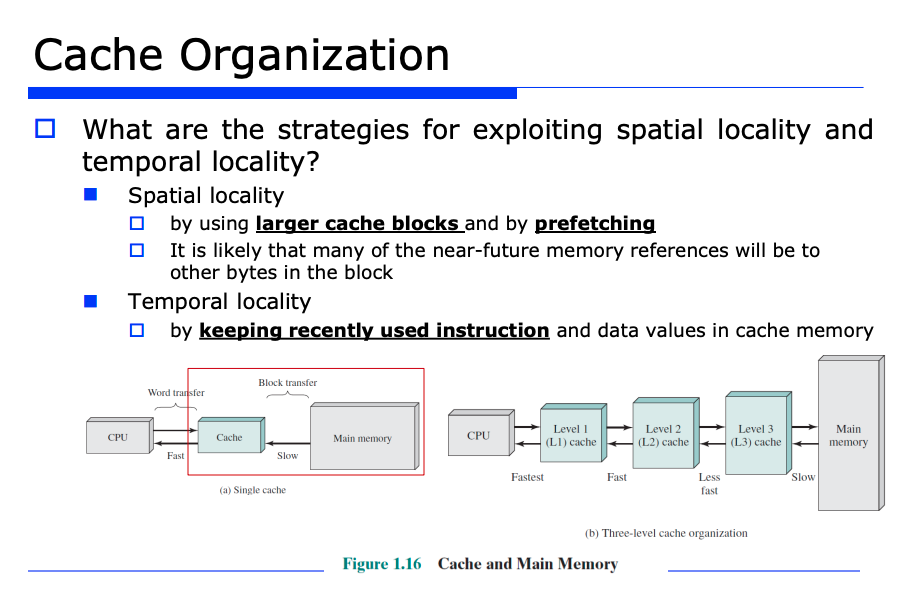
아까 이론적인 근거로 locality 를 살펴봤고, 시간적/공간적인 2가지 locality 를 살펴봤다. 이때 미래에 참조될 확률이 높은 데이터를 프로세서 근처에 배치할 수 있도록 캐시를 구성해야한다.
또 시간적/공간적인 2가지 locality 를 만족시키기 위해서 배치를 잘 해야한다.
캐시에 대한 spatial(공간적) locality 를 만족시키는 방법
일단 공간적인 locality 를 만족시켜야한다. 공간적인 locality 란 앞서 말했듯이 참조된 데이터의 근처에 있는 데이터들도 미래에 참조될 확률이 높다는 것을 가정하는 것이였다. 따라서 미리 참조될 데이터 근처에 있는것을 모두 fetch 한다 (캐시에 올려놓는다).
블럭(block) 단위의 연산 진행
이렇게 한다면 반복문 같은걸로 배열 원소들을 조회할때 locality 를 확인할 수 있을것이다. 또 이것은 곧 블럭화 했다는 것이다. 우리가 보통 메모리에 access 해서 word 단위로 할텐데, 가령 32bit 는 4byte 단위로 블럭화할텐데 이렇게 블럭 단위로 묶자는 것이 핵심이다. 즉, 블럭 단위로 연산이 진행된다.
캐시에 대한 temporal(시간적) locality 를 만족시키는 방법
그러면 temporal locality 는 어떻게 만족시킬까?
temporal locality 란 한번 접근한 데이터는 미래에도 다시 또 접근할 확률이 높은것을 기대하는 것이였다.
즉 한번 참조되면, 이왕이면 캐시에 저장해 두는것이다. 한번 요청이 왔을때 miss 가 발생하면 하위계층에 있는 그 데이터를 캐시에 옮기는 것이다.
또한 이 외에도 캐시가 꽉 찼을때 캐시에 있는 기존 데이터중에 어떤 데이터를 버리고 새로운 데이터를 캐시에 넣어야할지와, 어떤것을 더 자주 사용되는 데이터로 판단해야하는지의 알고리즘등 temporal locality 를 만족시키기 위한 여러가지 고려사항이 존재한다.
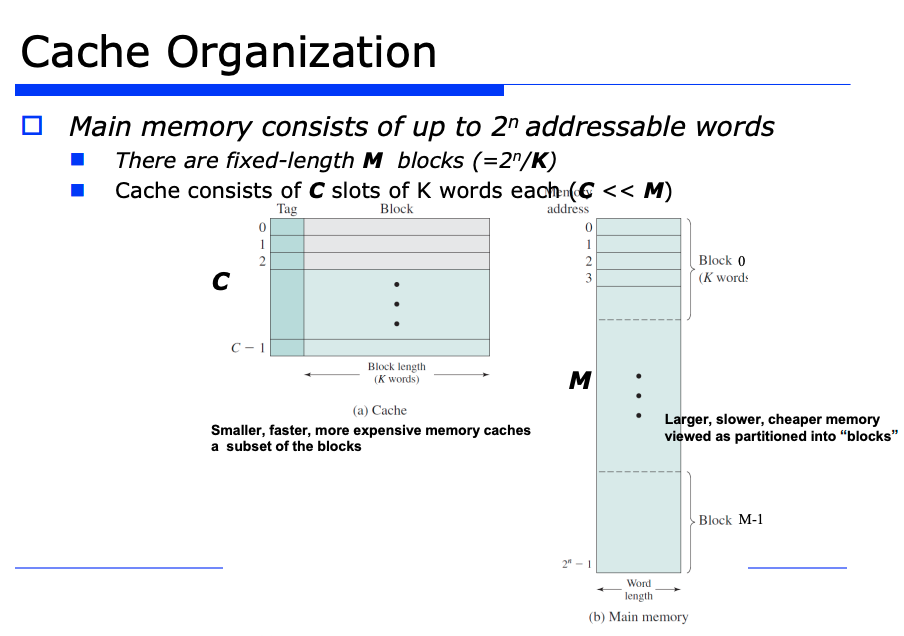
또 고려해야할 중요한 사항은 블록(block) 의 크기이다. 얼만큼의 크기를 한 블록 단위로 잡을것인가가 캐시의 구성요소가 될것이다.
위 그림을 보면, 이 locality 를 캐시 구성에 반영하기 위해서 블럭 단위로 처리해야 한다는 것을 알수있다.
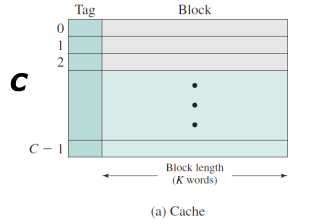
위 그림은 상위계층의 구성요소이고,
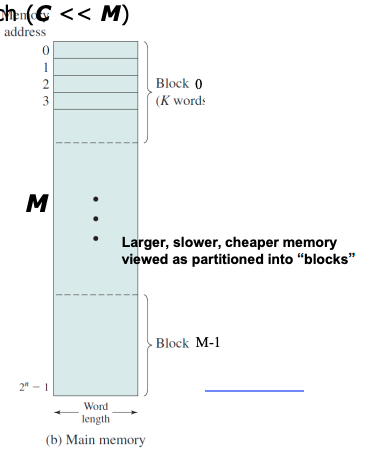
또 위 그림은 하위계층의 구성요소라고 가정해보자.

또 메모리에 2^n - 1 개의 word 가 있다고 가정해보자.
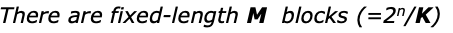
그리고 각 블럭은 k개의 word 로 묶는다. 즉 메모리의 크기(word의 총 개수) 인 2^n 를 k개로 나누면 M이 나온다. M개의 블럭이 메모리에 존재하는것이다.
=> 정리하자면, 메모리에 총 M개의 블럭이 존재하고 각 블럭에는 k개의 word 가 들어있다.
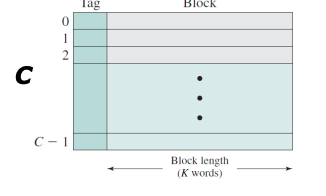
또 캐시의 블럭의 개수를 C 개라고하고 각 블럭에는 K 개의 word 가 들어있는 상황을 가정해보자.

그렇다면 C 는 M 보다 작을것이다.

Mapping Function & Directed Mapped Cache
Mapping Function 이란 무엇일까?
우리 눈에는 캐시의 각 라인이 블럭으로 보이는데, Mapping Function 이 뭔지 이해하기 위해 K = 1 이라고 가정하자. K = 1 이라는 것은 곧 한 블럭은 1개의 word 로 구성된다는 것이다. 또 지금 그림을 보면 tag 라는 용어가 등장했다. 이것도 이해해야한다.
일단 Mapping Function 이란 캐시에서 특정 블럭이 어디에 위치할지를 결정 (주소를 저장) 하는 것이다. Directed Mapped 방식이라는 것이 있다. 이건 또 뭘까?
K=1 이므로 Mapping Function 에서 각 인덱스 번호를 캐시의 블럭번호라고 보자. 또 C=8, M=32 라고 가정해보자.
당연히 C(캐시의 블럭 개수)가 M(메인 메모리의 블럭 개수)보다 훨씬 작기 때문에, 당연히 충돌이 발생할 수 있다.
또 자리 배치를 어느정도는 약속된 공간의 위치를 결정할 수 있는 Mapping Function 이 필요하다. 이때 자리 배치방법의 가장 심플한 방법은 나머지 연산 "mod" 를 사용하는 것이다. 이때 나머지 연산자는 캐시의 크기인 C = 8 이다. 예를들어 인덱스 번호 0 에 대해서는 0 % 8 = 0 을 진행해서 캐시의 0번째 인덱스의 블럭과 메인 메모리의 특정 인덱스가 매핑되는 것이다.
이렇게 미리 function 을 정의하고 사용하는 방식을 Directed Mapped Cache 라고한다.
Tag

tag 는 무엇일까? 예를들어 캐시에 어떤 데이터가 있다면 앞선 예제에서는 4개중 하나일것이다. 그 4개중에 어느것인지 구분해야할텐데, 이를 위한 식별자가 바로 tag 이다. 순수하게 Mapping Table 만 사용하면 mapping table 의 4개의 인덱스 방이 동일한 캐시 블럭을 참조하기 때문에, 정확히 누구에 대한 것인지 구분이 필요해서 tag 를 구분자로써 사용하는 것이다.
tag 값으로 어떤 것인지 구분하는 예제는 다음과같다. 예를들어 tag 값이 3일 경우를 생각해보자. 또 캐시의 0번 인덱스의 블록과 매핑되는 것은 Mapping Table 에 4개의 요소(0, 8, 16, 24) 가 있다. 모두 캐시의 동일한 블록을 가리키고 있는데, 이때 나머지 연산 "%" 이거말고 나머지 연산 "/" 을 통해 tag 값과 동일한 결과가 나오는 것이 바로 주인이다.
0/8 = 0 이고, 8/8 = 1이고, 16/8 = 2이고, 24/8 = 3 이다. 이때 24에 대한 나누기 연산이 tag = 3 값과 일치하므로 24가 주인이다.
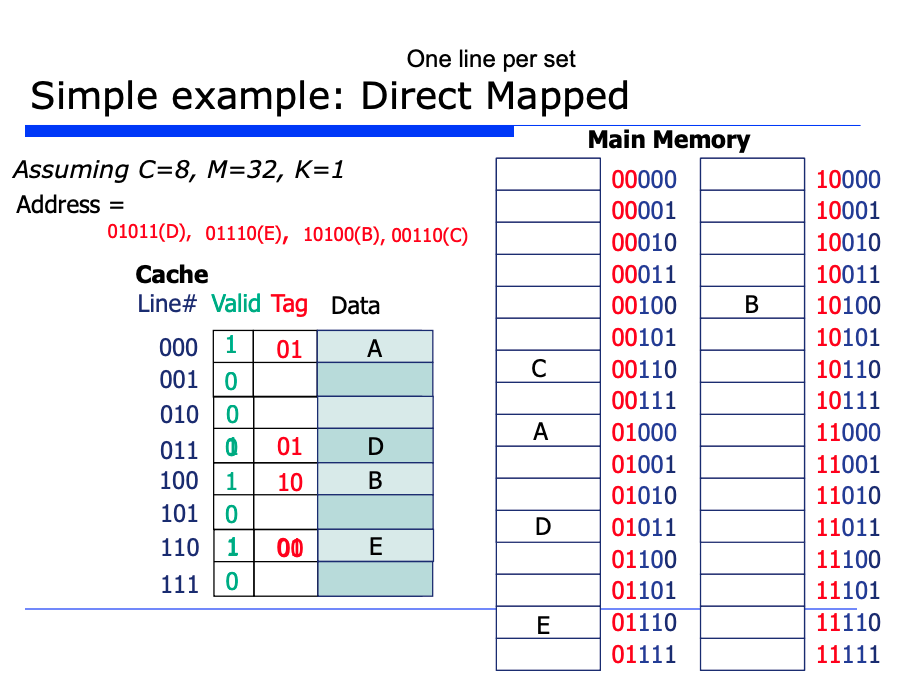
예시를 보자. 이때 valid bit 이라는게 추가되었다. valid bit 이란 캐시에 블럭이 있을수도 있고 없을수도 있는데, 캐시에 있는지 없는지를 나타내는 1 bit 이다.
Directed Mapped 방식에서 보듯이 캐시의 각 라인 단위의 주소에 대한 구성성분은 3bit 로 구성되어있다. (valid bit => 1bit + tag => 2bit = 3bit )
즉 캐시는 8가지의 라인 단위로 구성되어 있는것이다.
이에대한 주소 표현 및 매핑을 위해, 메인 메모리의 5 bit 중에서 끝의 3 bit 는 이러한 캐시의 8가지 라인 단위의 주소를 매핑하기 위해 사용된다.

자, 그러면 처리기(Processor) 에서 메모리에 접근할때가 있을것이다. 이때 주소값이 위와같이 주어졌을때의 매핑되는 캐시의 블럭을 어떻게 조회할까?
-
01011(D) : Processor 는 뒤의 3 bit 인 011 를 확인하게 되고, 캐시의 011 번지로 찾아간다. tag 값이 01 로 동일하므로 hit 이 발생한다. 따라서
-
01110(E) : 뒤에 3 bit 를 확인해보면 110 이다. 캐시의 110 번지 라인을 가보면 Tag 값에는 00 이 채워져있다. 그런데 캐시에 들어있는 이 Tag 값 00 과, 01110 에서 Tag bit 인 01 은 서로 다르므로 miss 가 발생한다. 따라서 Processor 는 메인 메모리로부터 데이터 E 를 읽어오고, 캐시의 해당 라인의 Tag 비트를 00 에서 01 로 최신화한다. (최신화하는 이유는 가장 최근에 읽어온 데이터가 미래에 더 자주 사용될 데이터라고 판단되기 때문)
-
10100(B) : 캐시의 100 번지 라인으로 가본다. 10100 에서 tag 비트 10 과 캐시에 들어있는 tag 값이 10 으로 일치하므로, hit 된다. 이로써 Processor 는 메인 메모리까지 안가도되고, 캐시에서 바로 빠르게 데이터 B 를 읽어오게 되는 것이다.
-
00110(C) : 캐시의 110 번지 라인으로 가본다. 그런데 tag 비트값이 다르므로 miss 가 발생한다. 따라서 Processor 는 메인 메모리의 00110 번지에 있는 데이터 C 를 번거롭게 읽어와야한다.
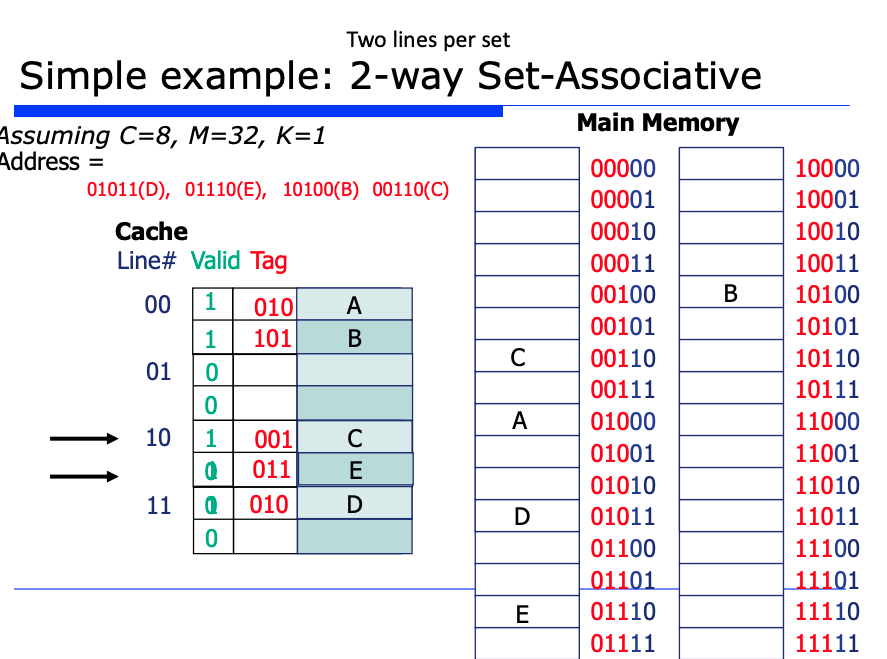
총 8개의 라인이 있는데, 2개의 라인을 하나의 set (집합) 으로 보자는 것이다. 그렇다면 위처럼 4개의 set 이 나오게 될 것이다.
집합, 즉 라인이 4개가 되었으므로 라인을 구분할 bit 는 2개면 된다. 아까는 라인이 8개였으므로 bit 가 3개가 필요했으나, 이제는 2개의 bit 만 있으면 2^2 = 4개의 라인 수를 구분할 수 있게된다.
반면 tag 는 3bit 가 되었다. 왜냐면 한 라인에 들어갈 수 있는 경우의 수가 8가지로 늘었기 떄문이다.
이제 캐시에 데이터를 넣을 때, 한 라인(집합)에 2개의 줄의 아무곳에나 삽입하면 된다. 2개의 줄이 모두 비어있는 경우는 순차적으로 한 줄에다 데이터를 넣으면되고, 1개의 줄이 비어있는 경우라면 이미 채워져있는 줄 말고 비어있는 줄에다가 데이터를 넣으면된다.
또 둘다 꽉찬 경우라면 두 줄 모두에 대해 tag 값 비교하면서 hit 날지 miss 날지 판단해주면 된다.
집합(set) 에 라인이 증가함에 따른 장단점
그런데 이렇게 한 라인(집합)에 줄이 2개로 늘면서, 탐색을 해야하는 상황이 발생수 있다. Directed Mapped 의 경우 한 줄만 확인하면 끝이였지만, 이 경우는 두 줄 모두 확인해야하는(탐색해야하는) 번거로움이 존재한다. 이로인해 오버해드가 발생하게 된다.
=> 한 라인(집합)에 줄이 늘어날수록, 즉 n-way Set-Associate 에서 n 값이 커질수록
- 단점 : 탐색 비용이 늘어서 비용이 증가될 수 있다. (오버해드 발생)
- 장점 : hit rate 이 증가할 수 있다.

캐시를 디자인시 가장 중요한 3가지 요소를 짚고 넘어가자.
-
mapping function 의 flexability (유연성) : 앞서 말했던 내용이다. 집합(set) 의 라인의 수에 따라서 비용이 증가할 수도 있다는 것이다.
-
캐시의 크기 : 캐시의 크기는 무조건 커진다고 좋은것이 아니다. 커질수록 앞서 봤던 n-way cache 에서 n이 커지면 오버해드가 발생할 수 있다.
- 블럭(block) 의 크기 : 블럭의 크기는 공간적인 locality 를 만족시키기 위해 만든것인데, 이 크기가 엄청 커지면 반복문 같은것을 수행시 일시적으로 hit rate 이 증가할 수 있다. 그러나 반복문이 다 끝나면 캐시에는 원하는 데이터들이 없어서 miss rate 이 엄청 증가할 수 있다. 따라서 블럭의 크기는 적절히 조절해야한다.
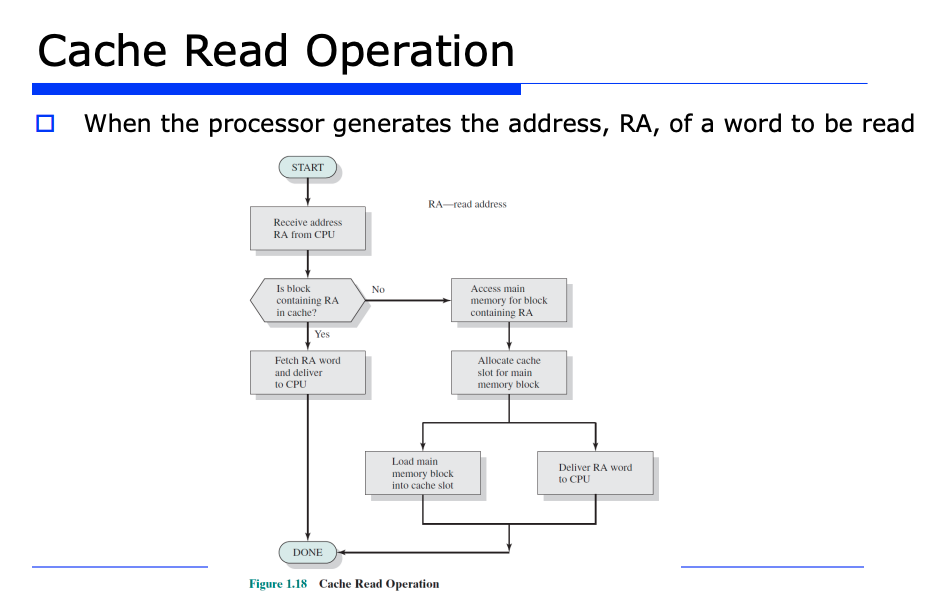
캐시의 Read 연산에 대해 살펴보자.
처리기(Processor) 가 fetch, Load, Store 등을 메모리에 대해 진행하면서 여러 주소가 나오게될것이다.
아무튼 CPU 로 부터 주소를 받고 캐시를 확인해본다. 확인했더니 캐시에 존재하는 블럭이라면 hit 가 발생하면서 CPU 에게 바로 데이터가 즉각적으로 리턴되는 것이다.
반대로 캐시에 없는 블럭이라면 메인 메모리에 접근해서 데이터를 가져오고, temporily locality 를 위해서, 즉 방금 메인메모리에서 읽어온 데이터가 또 쓰일 수 있다는 가정하에 캐시에 블록으로써 저장한다.

Write 연산은 우리가 프로그램에서 캐시를 쓸 때 크게 2가지 전략이있다.
write 연산을 하려고 캐시에 갔더니, 캐시와 메모리를 모두 업데이트해야한다. 이 업데이트를 동시에 하는 전략이 있다. 또는 늦추는 delay 전략이있다. 즉 캐시에만 쓰고 실제 메모리에는 최대한 나중에 쓰는 전략이다.
- write-through : 캐시 뿐만 아니라 메모리에도 바로 즉각적으로 write 하는 전략
- write-back : 캐시에만 쓰고, 메모리에는 나중에 적절한 타이밍에 write 하는것
write-back 은 multi-processor 일때 문제가 발생한다. 메모리가 shared 메모리이고, 여러 CPU 가 접근해서 동시해 write 연산을 할 수 있는 상황인것이다. 따라서 일관성 측면에서 문제가 발생한다. 또 메모리에는 CPU 의 processor 외에도 I/O 디바이스, 즉 DMA 도 write 할 수 있다.

Multi-Processor 일때의 상황를 생각해보자.
CPU 3개가 있고 어딘가에 X=24 라는 데이터가 있다.
- 이때 CPU1 의 Processor 1 이 X=24 값을 읽어온다. 그러면 캐시에 24를 저장한다.
- 또 Processor 2 도 X=24 값을 읽어온다.
- Processor 1 이 X 를 32 로 write-back 하려고한다. 그러면 본인의 캐시에만 write 가 적용되고, shared memory 에는 업데이트가 반영이 안되서 일관성 문제가 발생할 수 있는것이다.
=> write-through 라고 해도 완전히 해결되는 것도 아니다. 따라서 하드웨어적으로 동기화 작업이 필요하다. 이런 문제를 일관성 문제라고 한다.