로또 당첨번호에 나온 번호는 모두 균일하게 나왔을까?

개요

로또를 사는 누구나 일확천금을 꿈꾸며 자신이 가지고 있는 번호들이 당첨번호와 일치하길 바란다. 혹자는 지난 회차들의 당첨번호를 보면서 많이 나온 번호들 또는 반대로 적게 나온 번호들로 로또 번호를 찍기도 한다. 이 글에서는 지난 회차들에서 가장 많이 나온 번호와 가장 적게 나온 번호를 나열하고, 이들의 확률이 균일한 편인지 검정해볼 것이다.

데이터 수집

2021년 1월 13일 기준으로 현재까지 총 944번의 로또 추첨이 시행되었다. 이 당첨 번호들은 동행복권(dh.lottery.co.kr)에서 제공하는 api를 호출하여 가져와서 csv로 저장했다. 코드는 다음과 같다.

library(httr)
library(jsonlite)
basic_url <- 'https://www.dhlottery.co.kr/common.do?method=getLottoNumber&drwNo='
df_lotto_num <- NULL
for (x in 1:944) {
  req_url <- paste0(basic_url, x)
  df_response <- as.data.frame(fromJSON(req_url))
  df_sub <- subset(df_response, select = c("drwNo", "drwtNo1", "drwtNo2", "drwtNo3", "drwtNo4", "drwtNo5", "drwtNo6", "bnusNo"))
  if(x == 1) {
    df_lotto_num <- df_sub
  } else {
      df_lotto_num <- rbind(df_lotto_num, df_sub)
  }
  print(paste(x , "crawled."))
}
write.csv(df_lotto_num, "./lotto.csv")

전처리

lotto.csv에서 데이터를 읽어와서, 각 회차별 보너스 번호를 제외한 6개의 번호들만 추출한다. 그 다음, 1~6번째 번호별로 1부터 45까지의 번호가 얼마나 나왔는지 total() 함수로 집계한 뒤, 이를 다시 합쳐서 집계했다. 코드와 집계된 데이터프레임은 다음과 같다.

df_lotto_num <- read.csv("./lotto.csv")
df_lotto <- subset(df_lotto_num, select = c("drwtNo1", "drwtNo2", "drwtNo3", "drwtNo4", "drwtNo5", "drwtNo6")) #보너스 번호는 제외
df_count <- apply(df_lotto, 2, table)
df_sum <- NULL
for(item in df_count) {
  if(is.null(df_sum)) {
    df_sum <- as.data.frame(df_count$drwtNo1)
  } else {
    df_item <- as.data.frame(item)
    df_sum <- rbindlist(list(df_sum, df_item))[,lapply(.SD, sum, na.rm=TRUE), by = Var1]
  }
}
df_sum

##     Var1 Freq
##  1:    1  132
##  2:    2  124
##  3:    3  126
##  4:    4  129
##  5:    5  128
##  6:    6  118
##  7:    7  125
##  8:    8  127
##  9:    9   95
## 10:   10  131
## 11:   11  128
## 12:   12  135
## 13:   13  134
## 14:   14  133
## 15:   15  127
## 16:   16  123
## 17:   17  136
## 18:   18  137
## 19:   19  130
## 20:   20  132
## 21:   21  125
## 22:   22  107
## 23:   23  113
## 24:   24  124
## 25:   25  122
## 26:   26  125
## 27:   29  114
## 28:   35  115
## 29:   27  139
## 30:   28  117
## 31:   30  112
## 32:   31  127
## 33:   32  110
## 34:   33  131
## 35:   34  146
## 36:   36  126
## 37:   37  128
## 38:   38  127
## 39:   39  136
## 40:   40  134
## 41:   41  114
## 42:   42  123
## 43:   43  140
## 44:   44  126
## 45:   45  133
##     Var1 Freq

시각화

먼저 로또 번호별 등장 개수를 막대 그래프로 시각화해봤다.

library(ggplot2)

ggplot(df_sum, aes(df_sum$Var1, df_sum$Freq))+geom_bar(stat = 'identity')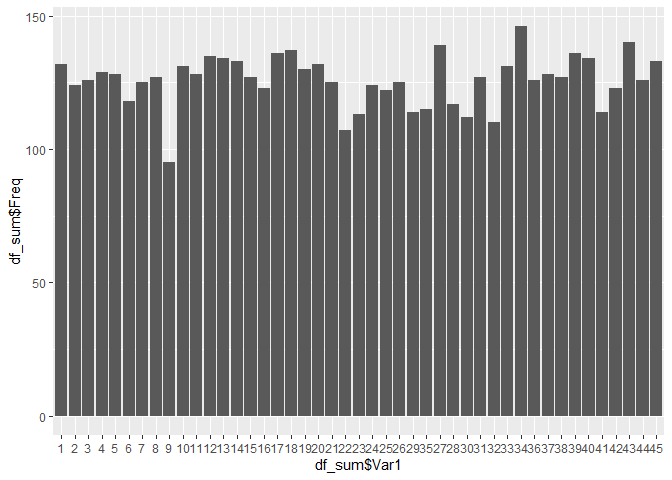

이 등장 개수들을 오름차순으로 다시 정렬해보면,

ggplot(df_sum, aes(x=reorder(Var1, Freq), y=Freq))+geom_bar(stat = 'identity')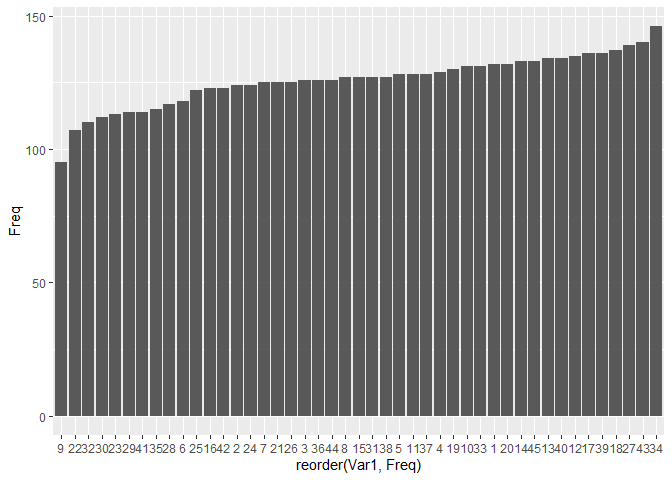

34번이 가장 많이 등장했고, 9번이 가장 적게 등장했음을 알 수 있다.

검정

지금까지 나온 번호들이 모두 균일하게 나왔는지에 대해, 카이제곱검정을 통해 검정할 수 있다. chisq.test() 함수로 검정해 본 결과,

chisq.test(df_sum$Freq)

## 
## 	Chi-squared test for given probabilities
## 
## data:  df_sum$Freq
## X-squared = 32.552, df = 44, p-value = 0.8985

카이제곱 값(X^2)은 32.552, 자유도(df)는 44, 유의확률(p-value)는 0.8985의 값이 나왔다. 이때, 신뢰수준을 95%로 가정하면, 유의수준(alpha level)은 0.05가 되고, 이는 유의확률보다 매우 작다. 다시 말해, 95%의 신뢰 수준에서, 로또 당첨번호별 등장 확률은 균일하다고 볼 수 있다.

결론

어느 번호가 더 많고, 어느 번호가 더 적게 나왔지만, 그럼에도 번호별 등장 확률은 균일하다는 검정이 나왔다. 아무래도 로또 1등이 되는 방법은 하늘에 기도하는 방법밖에 없는 모양이다 :(