[백준] #2166. 다각형의 면적

문제는 여기서 확인할 수 있다. BaekJoon #2166. 다각형의 면적

문제 파악

• 외적을 이용한 다각형의 면적 구하기
• long long 또는 long double 타입으로 오버플로우 방지

---

💀 시행착오

문제에서 좌표를 주니 당연스럽게 닫힌 다각형이 나올 것이라고 생각했다. 하지만 틀렸습니다를 세 번이나 마주하고 질문 검색 확인해보던 중 ??스러운 글을 발견했다.

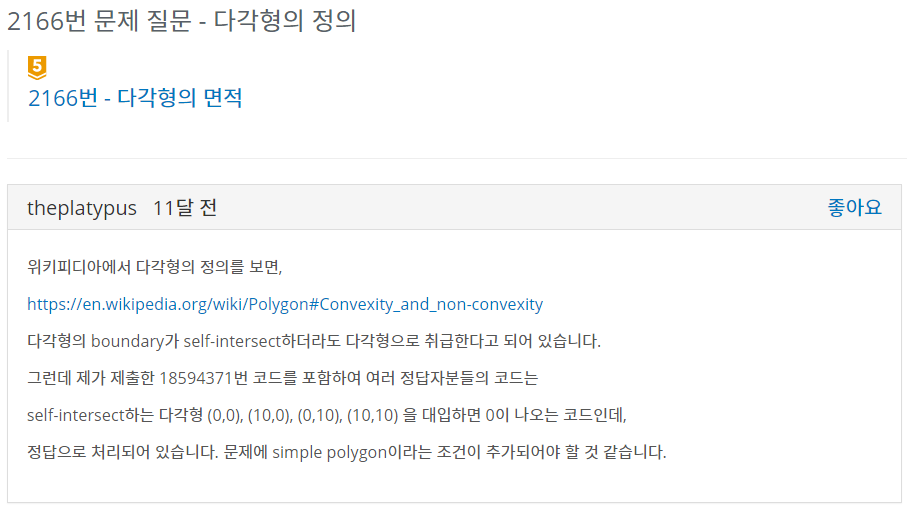
요약하자면 self-intersecting polygon에 대해 정답이 0이 나오게 된다는 것.
예제 입력1 을 이용해 설명해보겠다.

예제 입력 1
4
0 0
0 10
10 10
10 0

위 결과는 100.0이 나온다. 하지만 아래의 결과는 0.0이다.

self-intersecting polygon 예제
4
0 0
0 10
10 0
10 10

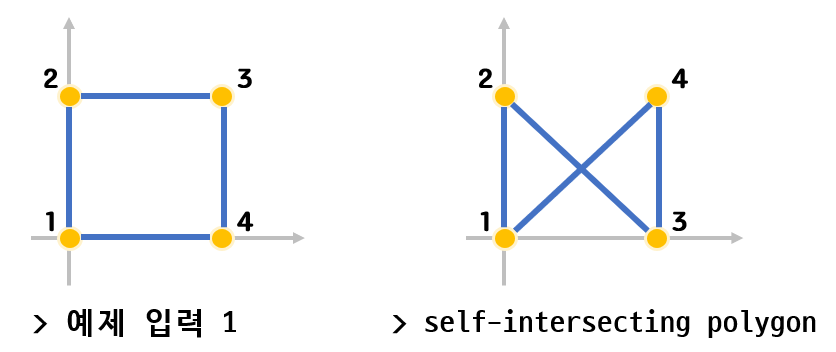
두 예시의 차이는 좌표의 순서뿐이다. 문제에 순서대로 그린다는 조건은 없었지만 순서를 무시하고 계산했을 경우에는 틀렸습니다가 나오는걸 봐서는 순서를 고려해서 self-intersecting polygon을 찾을 수 있을 것 같다. 사실 외적 계산은 양/음수가 구분되서 알아서 self-intersecting polygon의 결과가 0.0이 나온다.
암튼 이걸 모르고 외적 결과를 양수 처리해서 두번째 예시도 100.0이 나오도록 만들었다가 괜히 틀렸습니다를 많이 만났다.

---

🤔 풀이과정

외적

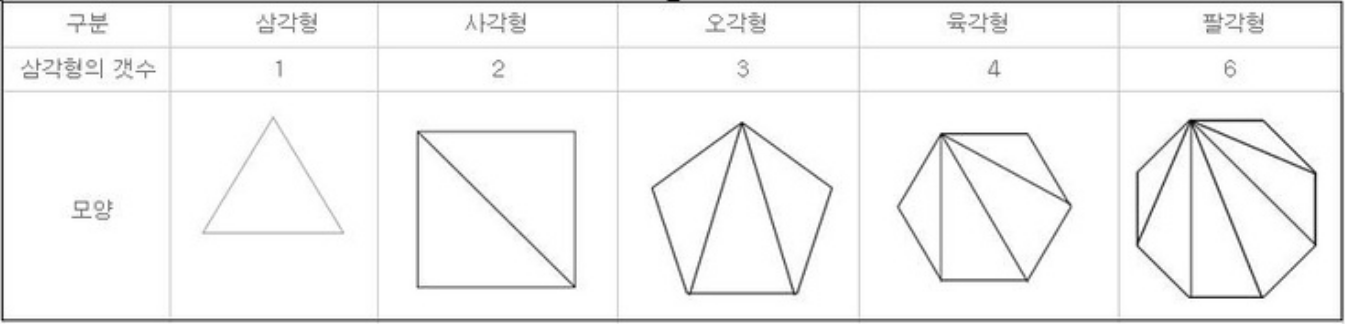
초등학생 때 다각형의 넓이는 삼각형으로 나눠서 구할 수 있다고 배웠다.
그리고 세 점으로 이루어진 삼각형은 두 벡터로 만들어지는 평행사변형의 반이다. 그리고 이 평행사변형은 외적으로 구할 수 있다.

벡터에는 기준이 있어야하니 처음으로 들어오는 점을 기준으로 잡고 이후 두 점씩 잡아서 외적을 구했다. 그러면 self-intersecting하지 않는 경우에는 서로 겹치지 않는 삼각형들을 구할 수 있다.
self-intersecting polygon의 경우 외적을 구하다보면 음수가 나와서 알아서 0.0 결과가 나온다!

long double type

문제 파악에서 얘기했듯이 좌표범위가 절댓값 100,000 미만이다. 따라서 계산 범위가 int를 넘어갈 수 있다. long long을 쓸 수도 있지만 외적값을 반으로 나누기 때문에 long double을 쓰는 것이 편리하다.

코드

전체 코드는 아래와 같다.

//BaekJoon_2166
//다각형의 면적
/*
* 제한 시간 : 2s
* 정답 비율 : 23.645%
*/

#include <iostream>
#include <vector>
#define ld long double
using namespace std;

struct loc{
    ld x, y;
};

void get_input(int &n, vector<loc> &points){
    loc temp;
    scanf("%d", &n);
    for(int i=0; i<n; i++){
        scanf("%Lf %Lf", &temp.x, &temp.y);
        points.push_back(temp);
    }

    return;
}

// 외적 계산
ld ex_product(loc stand, loc pa, loc pb){
    ld result = 0;
    result = (pa.x-stand.x)*(pb.y-stand.y) - (pa.y-stand.y)*(pb.x-stand.x);  
    return result / 2.0;
}

ld calc_area(int n, vector<loc> &points){
    ld area = 0;
    loc standard_point = points[0]; // 기준 점

    for(int i=1; i<n-1; i++){   // 두 벡터의 외적 계산
        area += ex_product(standard_point, points[i], points[i+1]);
    }
    return area;
}

int main(){
    int n;
    vector<loc> points;

    get_input(n, points);
    ld result = calc_area(n, points);
    if(result < 0) result *= -1;
    printf("%.1Lf\n", result);

    return 0;
}

---

끝 ✌