일단 재귀함수의 개념도 다시 짚고 가야했다.
1. 문제 설명

문제 상황은 토너먼트 상황이다. n은 참가하는 참가자 수이고, a와 b의 값은 각각 a와 b가 참가하는 순서이다. 여기서 문제는 a와 b가 무조건 각 토너먼트에서 승리하고 올라간다면, 언제 2명이 경쟁하는 순간이 오느냐이다.
그림으로 보면 다음과 같다.

노란색 네모가 최초의 4번째 참가자인 a이고, 연두색 네모가 최초의 7번째 참가자인 b이다. a와 b가 대결을 하게 되는 순간은 3번째 경기 과정이고 문제에서는 이 3번째를 구하는 함수를 요구한다.
2. 어려웠던 점
1) 재귀함수 return
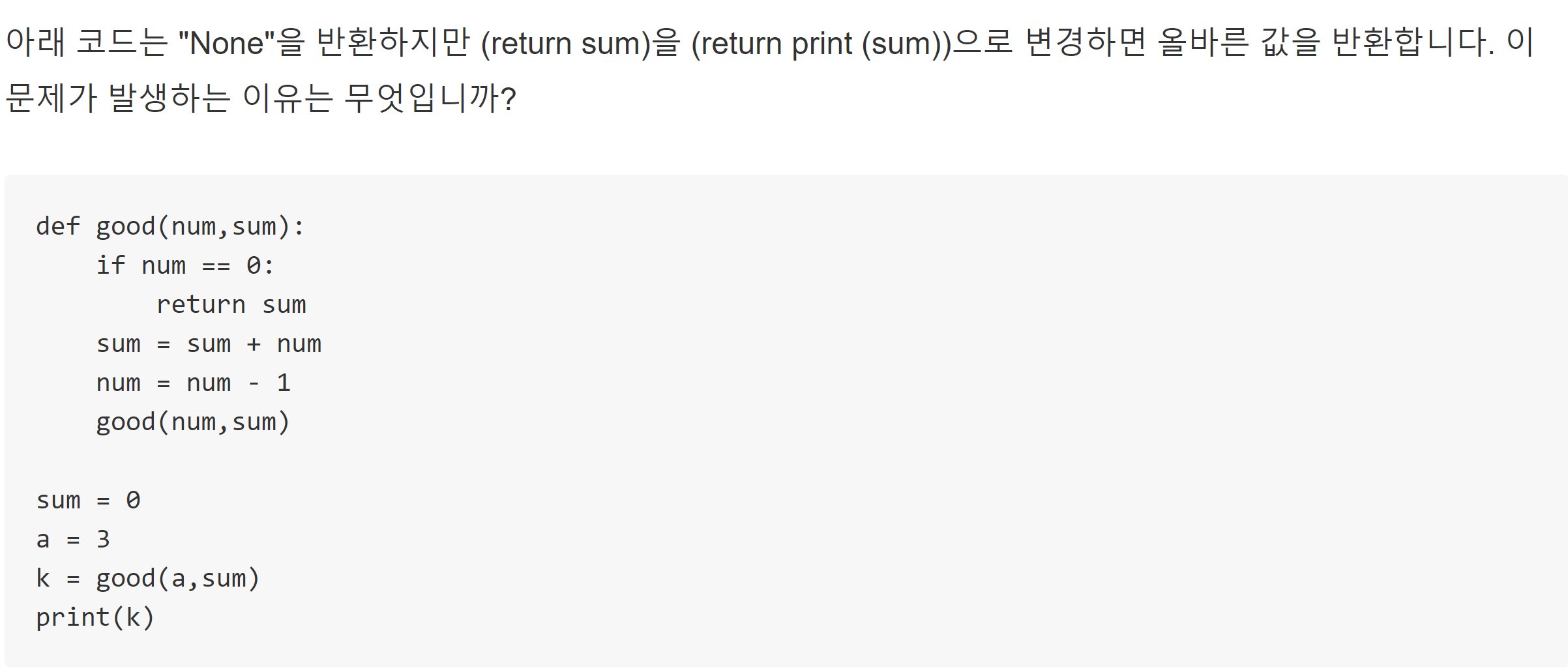
처음에 코드를 이렇게 작성했는데, None을 리턴하게 되었다.
def dfs(n, a, b, cnt):
if abs(a - b) == 1:
return cnt
n = n // 2
a = a // 2 + a % 2
b = b // 2 + b % 2
cnt += 1
dfs(n, a, b, cnt)
def solution(n, a, b):
return dfs(n, a, b, 1)
도대체 왜지..?
검색하다가 나와 비슷한 상황을 발견했다.

이런 내용이었다. 나도 위의 글쓴이처럼 재귀를 실행할때 재귀 함수 호출을 리턴형식으로 사용하지 않았다. 사용한적도 거의 없고, 재귀를 빠져나와야 하는 조건에서만 ret을 쓰면 된다고 생각했다.
하지만, 어쨌든 오류가 발생했다는 것은 내가 잘못 알고있다는 증거이다.
관련된 내용을 게시글로 포스팅했다.
2) 조건
처음에 재귀를 종료하는 조건에 다음과 같은 if문을 사용했다.
def dfs(n, a, b, cnt):
if abs(a - b) == 1 and n ==2: -> 이거
return cnt
n = n // 2
a = a // 2 + a % 2
b = b // 2 + b % 2
cnt += 1
dfs(n, a, b, cnt)
def solution(n, a, b):
return dfs(n, a, b, 1)
근데, 오류가 발생했다. 생각해보니 n==2일 필요는 없다. 단순히 토너먼트를 하다가 a와 b가 만나기만 하면 되는 문제였다. 아무튼 나의 착각...
3. 풀이
아이디어
일단, 주어진 a와 b는 무조건 토너먼트에서 승리하게 된다.
이 말을 자세히 생각해보면, a가 최초에 4였지만 그 다음 라운드에서는
무조건 2로 나눈 값으로 줄어든다는 의미이다.
왜냐면, 그 다음라운드에서는 전체 인원수가 절반으로 줄어들고, 당연히 a도 2로 나눈 순서가 된다. a앞에 몇명의 인원이 있더라도 그 중에서 절반만 다음 라운드로 올라온다. a도 그 절반이 되는 사람 중 하나임으로 당연한 얘기이다. (이걸 당연하게 받아들이지 못하면, 토너먼트 순서를 직접 그리면서 이해해야 한다.)
그래서 a가 이기게 되면 다음 a의 순서는 a = a//2+ a%2 이다.
여기서 나머지를 붙인 이유는 간단하다. 예를들어 a가 7이었다고 하면 a는 4가 된다. a가 8이었다고 해도 a는 4가 된다. a가 2로 나눠떨어지는 구간과 그 사이는 모두 몫의 범위가 된다. 즉, 7과 8은 4로써 같은 구간이 되기 때문에 나머지를 더해주는 것이다.
그런식으로 a와 b를 처리하고, 나머지는 재귀적으로 수행하도록 코드를 작성했다.
1) 1차 풀이
이렇게 했는데, 몇가지 경우에서 실패를 했다.
def dfs(n, a, b, cnt):
if abs(a - b) == 1:
return cnt
n = n // 2
a = a // 2 + a % 2
b = b // 2 + b % 2
cnt += 1
dfs(n, a, b, cnt)
def solution(n, a, b):
return dfs(n, a, b, 1)질문하기 게시판에서 여러가지 글을 찾아본 결과 다음의 경우
오류가 발생한다는 것을 알아냈다.
재귀를 종료하는 부분의 조건이 잘못되었다는 것을 알았다.
차이가 1이 날때 여기서 짝수, 홀수를 따져줘야 했다. 예를들어 ..
1. a = 4, b = 5
여기서 차이가 1이지만, 3번을 더 올라가야 하는 상황이다.
즉 (짝, 홀),(홀,짝) 인 경우를 다르게 처리해줘야 한다.
그리고, a가 b보다 항상 크다는 보장이 없었기 때문에
이런 처리가 필요했다.
2) 2차 풀이
def dfs(n, a, b, cnt):
if abs(a - b) == 1:
if a<b and a%2 ==1:
return cnt
elif a>b and a%2 ==0:
return cnt
a = a // 2 + a % 2
b = b // 2 + b % 2
cnt += 1
return dfs(n, a, b, cnt)
def solution(n, a, b):
return dfs(n, a, b, 1)