통계분석을 하기 전에는 데이터 사이의 기본적인 관계들을 탐색하여 초보적인 오류를 제거하는 데이터 탐사분석(EDA)를 수행할 필요가 있다.
EDA를 통해 각 변인들의 결측치나 이상치 등을 색출하고, 정규분포성 등 여러 분석의 기본 가정이 충족되었는지를 점검해야 한다.
(준비운동 같은거라고 보면 될듯?)
보통 각 변인에 해당하는 빈도, 최댓값, 최솟값, 평균, 표준편차, 왜도(분포가 횡적으로 얼마나 넓게 분포되어있나), 첨도(분포가 종적으로 얼마나 뾰족하게 분포되었는가)(뾰족할수록 좋은 데이터) 등등을 미리 알면 탐색하기가 수월하다.(기술통계)
df['구매가격'].describe()
#요약 통계 / 표준편차 : 평균에서 떨어진 정도 / median 중위값 /
#min,max의 차이가 크면 안좋아 중위값에 값이 많은게(집중경향치) 좋은 데이터
df['구매가격'].kurtosis() #첨도 /
df['구매가격'].skew()#왜도이 밖에 데이터들을 간단하게 matplotlib으로 시각화 해서 한눈에 알아보는 것도 유용하다.
EDA를 위한 기술통계가 끝나면 변인들의 관계를 규명하기 위해 변인들의 성격에 맞게 통계기법을 적용하여 분석한다.변인들은 측정하는 척도에 따라서 4가지로 구분한다.
명목척도(불연속변인) - 범주적으로 구분만 하는 수준(ex-남,여/서울,부산,대구)
서열척도(불연속변인) - 명목척도에서 어느 정도 서열(순서)이 있는 수준(ex-초,중,고)
등간척도 - 서열척도에서 측정 값 사이에 일정한 간격이 있는 척도(ex - 1점(전혀 없다)~5(매우 많다)
비율척도 - 등간척도에 절대영점의 속성이 더 추가된 수준의 측정(ex-스마트폰 구매가격 nnn'원')
*그럼 명목척도와 등간척도의 차이점은?
서열척도는 객체의 순서만을 나타내는 척도입니다. 예를 들어, 등급(A, B, C, D, F)이나 순위(1등, 2등, 3등)가 서열척도의 예입니다.
등간척도는 '객체 간의 거리가 의미 있을 때' 사용되는 척도입니다. 예를 들어, 온도(°C)나 시간(hr)이 등간척도의 예입니다.(....시간이 왜 등간척도야? 비율척도 아냐?)
*시간이 왜 등간척도인가...ㅡㅡ
시간(time)은 실제로는 비율척도(Ratio Scale)이지만, 통계학에서는 대게 등간척도(Interval Scale)로 간주하고 있습니다.
비율척도는 0이 존재하며, 두 객체 간의 거리가 비율로 표현될 수 있는 척도입니다. 시간은 0이 존재하지만, 일반적으로 시작점을 정하지 않아 비율로 표현하기 어렵습니다.
그러므로 통계학에서는 시간을 등간척도로 간주하고, 객체 간의 거리만을 표현하며, 비율 개념을 적용하지 않습니다.
*절대영점이란?
등간척도에서의 4점은 2점보다 2배만큼 더 크다고 말 할순 없지만 절대영점이 있는 비율척도에선 10만원은 20만원보다 두배 많다고 말할 수 있다.
명목척도, 서열척도 - 질적/불연속적/분류적 변인
등간척도, 비율척도 - 양적/연속적/수량적 변인
*질적 데이터는 어떤 개체에 대한 특성을 나타내는 데이터를 의미합니다. 양적 데이터는 어떤 개체에 대한 수치적 특성을 나타내는 데이터를 의미합니다. 질적 데이터는 순서, 비율, 거리 등의 개념이 적용되지 않지만 양적데이터는 적용 될 수 있습니다.
*그럼 수치적 특성이어야 양적이고 연속적이고 수량적인가? 불연속적이면서 수량적 변인일 순 없는가?
그렇지만은 않다. 수량적 변인은 객체 간의 거리가 있어야 하며, 불연속적이라는 것은 객체 간의 거리가 어느 정도 이상 증가하면 그 다음 값으로 이동하지 못한다는 것입니다.
예를 들어, 구입한 아이폰의 용량(GB)이 수량적 변인으로 간주될 수 있습니다. 이 변인은 객체 간의 거리가 존재하며, 증가할수록 용량이 더 많아집니다. 하지만, 아이폰의 용량은 64GB, 128GB, 256GB와 같이 특정 값만 가질 수 있어 불연속적입니다.
*헐 그럼 연속적이면서 분류적일 수도 있나?
연속적이면서 분류적 변인(Continuous and Categorical Variable)이 동시에 존재하는 것은 불가능합니다. 변인은 수치적 데이터(Quantitative Data)인지, 분류적 데이터(Categorical Data)인지 구분해야 합니다. 수치적 데이터는 연속적인 값을 가질 수 있지만, 분류적 데이터는 고정된 범주(category)만을 가질 수 있습니다.
즉, 불연속적이면서 수치적 특성을 가질 순 있지만 연속적이면서 분류적일 수는 없다~
먼저, 독립변인과 종속변인이란?
독립변인: 실험 결과에 영향을 줄 수 있는 변인( = 조작변인 + 통제변인 )
①조작변인 : 가설이 검증될 수 있도록 실험자가 의도적으로 변화시키는 변인
②통제변인 : 독립변인 중에서 조작변인 이외에 일정하게 유지시켜야 하는 변인
종속변인 : 조작변인이 변함에 따라 결정되어지는 '결과'
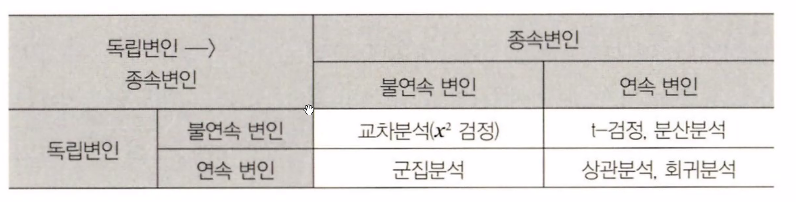
교차분석(X² 검정)
독립변인과 종속변인 모두 불연속 변인(명목척도 or 서열척도)이면 적용하는 통계방법
(ex-'스마트폰 브랜드'에 따라 '월수입'이 차이가 있는지?)
관찰빈도와 기대빈도(가설화된 빈도)를 비교하여 카이제곱값을 통해 통계적으로 검정한다.
카이제곱 검정(Chi-square test)에서 "변수"는 관측될 수 있는 특징이나 속성입니다. 예를 들어, 성별, 연령, 학력 등이 카이제곱 검정에서의 변수가 될 수 있습니다. 또한 카이제곱검정에서는 이산형 변수
"그룹"은 변수의 값에 따라 구분된 집단입니다. 예를 들어, 성별이 변수일 때 남성과 여성이 그룹이 될 수 있습니다. 카이제곱 검정에서는 각 그룹의 크기와 비율, 그리고 각 그룹에서의 특정 사건의 발생 횟수를 비교하여 귀무 가설이 성립할 확률을 검정합니다.
카이제곱 검정의 목적
먼저 카이제곱검정은 (보통)변수가 명목척도일 때하는데 이 때 데이터의 값은 빈도수가 된다.
변수가 한개인 경우 그룹간의 비율이 같은지 다른지를 볼 수 있고, 변수가 두개인 경우 변수 사이의 연관성이 있는지 없는지를 알 수 있다.
여기서 변수와 그룹이란?
카이제곱 검정(Chi-square test)에서 "변수"는 관측될 수 있는 특징이나 속성입니다. 예를 들어, 성별, 연령, 학력 등이 카이제곱 검정에서의 변수가 될 수 있습니다.
"그룹"은 변수의 값에 따라 구분된 집단입니다. 예를 들어, 성별이 변수일 때 남성과 여성이 그룹이 될 수 있습니다. 카이제곱 검정에서는 각 그룹의 크기와 비율, 그리고 각 그룹에서의 특정 사건의 발생 횟수를 비교하여 귀무 가설이 성립할 확률을 검정합니다.
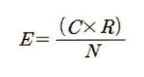
E = 기대빈도 (행과 열의 각 빈도의 합을 곱한 후 총 빈도수로 나눈 것)
기대빈도란?
뭘 기대하는거야? --특정 사건이 일어날 기대치입니다. 이 기대치는 각 사건이 독립적이고 같은 확률로 발생한다는 가정 하에 계산됩니다. ~~아 ~ 그럼 이건 귀무가설이구나~
#헷갈리지 말기
카이제곱검정에서 pvalue가 0.05 이상이면 귀무가설이 채택되므로 두 변수간의 유의성이 없다는 것이고 0.05이하면 귀무가설이 기각 되므로 유의성이 있다는 뜻이다!
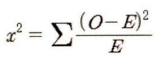
O는 관찰빈도
따라서, 카이제곱값은 관찰빈도인 O와 기대빈도인 E의 차이를 제곱한 후 기대빈도로 나눈 값. 교차분석 결과가 유의미한 값이 나온다면 독립변인에 따라 종속변인의 빈도분포가 통계적으로 차이가 있다고 간주할 수 있다.
pd.crosstab(df['월수입'], df['사용브랜드']) #열 속성 2개/ 교차분석사용브랜드 1 2
월수입
1 20 13
2 14 22
3 28 24
4 20 17
5 12 28
6 33 21
# 해석 : 월수입이 1인 경우 1브랜드를 사용하는 사람 20명 2브랜드를 사용하는 사람 13명...(관찰빈도를 구하는 거네)[in]
import numpy as np
fobs = df.월수입
fexp = df.사용브랜드
fexp = fexp * (np.sum(fobs)/np.sum(fexp)) #fexp 데이터의 값을 월수입의 값에 맞추어 수정하는 과정입니다.
chisquare(f_obs=fobs, f_exp=fexp)
[out]
Power_divergenceResult(statistic=343.26420150053593(카이제곱통계량), pvalue=9.618060771117479e-05(귀무가설확률))#0.05보다 낮으니 귀무가설 기각, 유의성 있음!# 카이제곱 분석
# - c: degrees of freedom
# - o: observed value
# - E :expected value
[in]
chisquare(df[‘구매장소’]. ddof=[0,1])
[out]
Power_divergenceResult(statistic=148.31174089068827,
pvalue=array([0.99999996, 0.99999995]))#각각의 자유도에 따른 결과자유도(degrees of freedom)는 통계학에서 분석에서 사용되는 개념으로, 얼마나 자유롭게 데이터가 변화할 수 있는지를 나타냅니다.
0인 자유도는 데이터의 개수가 고정되어 있거나 특정한 값을 충족해야 하는 경우에 해당됩니다.
1인 자유도는 개별 데이터 값이 하나씩 변경될 때마다 자유도가 감소하는 경우에 해당됩니다.
만약, 카이제곱 검정을 수행할 때 ddof=[0,1] 이라면, 두 개의 검정 결과를 가지게 되며, 각각 0인 자유도와 1인 자유도를 사용한 검정 결과입니다.
statistic - 통계량, 통계학에서 데이터에 대한 특정 정보를 수치로 나타낸 것입니다. 예를 들어 평균, 분산, 중앙값 등은 모집단의 특성을 나타내는 통계량입니다.
pvalue - 가설을 검정할 때 사용하는 확률값, 보통 pvalue가 0.05보다 낮으면 가설을 기각하고 높으면 가설이 의미 있다고 볼 수 있다.그렇지만 pvalue라고 무조건 귀무가설인 경우는 아니고 귀무가설인지 대립가설인지는 검정에 따라 달라진다.
아무튼!
카이제곱검정은 독립변수와 종속변수간의 유의미함을 알 수 있는 검정이고, 예시에서는 사용브랜드(독립변수)에 따라 월수입(종속변수)에 차이가 있는지를 측정하는 것이다.
(당연히 둘이 바꿔서 검정 할 수도 있음)
t-검정
t-검정은 독립변인이 불연속변인, 종속변인이 연속변인일 때 적용하는데 독립변인의 집단이 2개일 때만 적용한다.(여러개여도 두개만 지정해서 사용 가능)(*분산분석도 독립변인이 불연속변인, 종속변인이 연속변인일 때 사용하는데 보통 이 두개를 자주 쓴다.)
t-검정은 두 집단의 연속적인 변인의 평균값이 기대한 값과 실제 값 사이의 관계를 통해 검정하는데, 두 집단 간 평균의 차이 대 집단 변화량 사이의 비율이다.
모집단의 분산이나 표준편차를 알지 못할 때
모집단을 대표하는 표본으로부터 추정된 분산이나 표준편차를 가지고 검정하는 방법으로
“두 모집단의 평균간의 차이는 없다”라는 귀무가설과 “두 모집단의 평균 간에 차이가 있다”라는 대립가설 중에 하나를 선택할 수 있도록 하는 통계적 검정방법이다.
예시에서 명목변인은 사용브랜드, 비율변인은 구매가격, 등간변인은 재구매의향 에 통계적으로 의미있는 차이가 있는가 분석해 보는 것
(교육평가용어사전, 2004, 학지사)
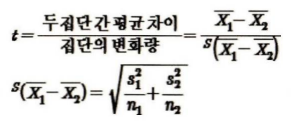
이 공식에서 분자는 표본의 평균과 가설화된 모집단 평균의 차이이고 분모는 평균에 대한 표준오차의 추정치이다.
X₁와 X₂는 각각 집단 1과 집단 2의 평균이고 s(X₁- X₂)에서 s는 표준오차이며, 따라서 s(X₁- X₂)공식에서는 n₁과 n₂는 각 표본의 크기를 나타낸다. 이 때 s(X₁- X₂)공식에서는 각 표본의 크기를 나타낸다. 즉 분산을 각 집단의 크기로 나눈 후 합산한 값에 루트를 씌운 것으로 이해할 수 있음
먼저 독립표본 검정을 해야하는데 이때 독립변인인 두 집단 사이에 균등하게 분산이 이루어져 있는가(등분산)를 먼저 검정한다.
[in]
sp.stats.levene(mean1, mean2) #H0: Normal Distribution을 따름,
Return(W, P-value)
# p-value가 0.0003 <0.05 >> 등분산성 가정 위배
[out]
Levene Result(statistic=13.443717170975082,
pvalue=0.00030027808643848084)위의 leven 검정결과값이 13.44...로 통계적으로 유의미한 차이가 있다고 볼 수 있고(statistic=13.44 > 0.05) 따라서 등분산가정은 따로 하지 않아도 된다.(equal_var=False)
[in]
stats.ttest_ind(mean1, mean2, equal_var=False) # Independent 2-sample t-test
# p-value 3.598124628532717e-17 < 0.05 귀무가설(무죄추정의 원칙 느낌)을 기각함 >> 차이가 있다.
[out]
Ttest_indResult(statistic=-9.2004623883404,
pvalue=3.598124628532717e-17)검정한 t값은 -9.20로 통계적으로 유의미한 차이(p=.00)가 있다고 해석된다. (sta
따라서 사용 브랜드와 구매가격에는 유의미한 차이가 있다.
이젠 브랜드애 따른 재구매의향의 차이를 알아보자.
[in]
sp.stats.levene(mean1, mean2) #H0: Normal Distribution을 따름, Return(W, P-value)
# 등분산성 가정 충족 (p-value > 0.05)
[out]
LeveneResult(statistic=0.1179597504462619,
pvalue=0.7315465812585951)얘는 등분산가정이 충족되었다.(statistic=0.1179597504462619 <0.05) 따라서 (equal_var=True)옵션이 들어가야 한다. 이렇게 재구매의향의 차이를 검정한 결과
[in]
stats.ttest_ind(mean1, mean2, equal_var=True) # Independent 2-sample t-test
# 유의미한 차이가 없음
[out]
Ttest_indResult(statistic=-0.0891603787635918,
pvalue=0.9290258377820513)
# p-value 0.9290258377820513 > 0.05 귀무가설 성립 / 차이가 없다!!분산분석
(*분산분석도 독립변인이 불연속변인, 종속변인이 연속변인일 때 사용하는데 보통 이 두개를 자주 쓴다.) 위에 t-검정에서 긁어옴 이 부분은 동일 하지만 t-검정은 독립변인의 집단이 2개일 때 적용하고 분산 분석은 3개 이상의 집단일 때 적용한다.
이 예시에선 연령이 1,2,3 으로 집단이 3개 이상이다.
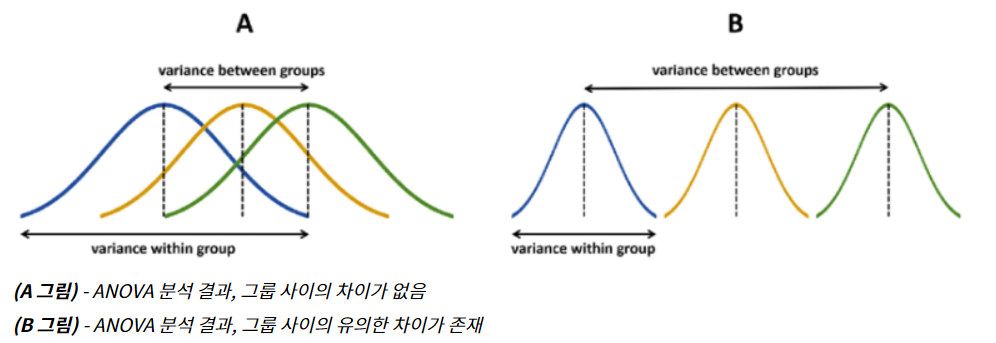
분산분석은 F값을 통해 검정하는데 집단 간 분산(변화량 혹은 변량)과 집단 내 분산과의 관계를 통해 계산한다.
집단 간 분산 - 각 집단의 평균에 대한 분산
집단 내 분산 - 각 집단 내에서 집단 내 평균에 대한 분석
F는 집단간의 차이가 없다면 집단 간 분산과 집단 내 분산이 같다는 의미이고 집단 내 분산이 집단 간 분산보다 클수록 각 집단은 차이가 있다고 간주한다.
F를 구하는 공식은 아래와 같다.
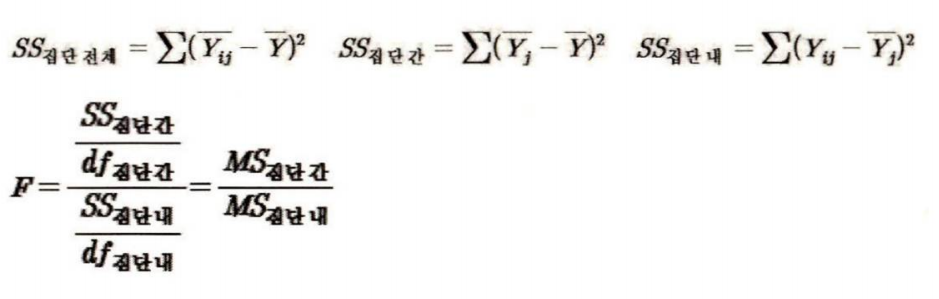
SS = 제곱 합, df = 자유도, MS = 평균제곱합(통계량)
즉, 제곱 합/자유도 = 평균제곱합
Y(ij)에서 첨자 i는 각 사례를(재구매의향, 구매금액) / j는 집단을 의미
Y = 관찰값?
SS(집단간) = 각 케이스의 종속변인 관찰값의 총 평균으로부터 각 집단 평균의 차이를 합산한 것이다.
SS(집단내) = 각 집단 간 평균과 각 집단 내 모든 사례가 갖는 종속변인의 Y 관찰값간 거리를 합산한 것이다.
자유도(degree of freedom)는 확률과 통계에서 표본의 수에 따라 결정되는 수치를 의미합니다. 자유도는 표본 분석에서 표본의 수에 따라 검정하는 규칙을 설명하는 용어로, 특정 통계 분석에서 표본 데이터에서 결정할 수 있는 변수의 수를 나타냅니다. 예를 들어, 평균값을 구하는 경우에는 표본의 개수 n에서 1을 뺀 자유도가 됩니다. 자유도가 높을수록 표본 데이터의 분산을 더 정확하게 측정할 수 있습니다.
알고싶은것 : 집단에 따라 현재 사용하고 있는 스마트폰에 대해 재구매의향이 차이가
있는가,그리고 스마트폰 구매금액이 차이가 있는가?
집단 간 분산 : 전체 재구매의향/ 구매금액 평균값과 3개 집단 각각의 재구매의향/ 구
매금액 평균값 사이의 변화량 차이
집단 내 분산 : 3개 집단 각각의 재구매의향/ 구매금액 평균값과 각 집단 내 사례들 사이의 재구매의향/ 구매금액 변화량 차이
이 두 값의 관계를 통해 3개 집단의 평균값이 차이가 있는가를 본다.
[in]
anova1=df[df['연령2']==1].재구매의향.values
anova2=df[df['연령2']==2].재구매의향.values
anova3=df[df['연령2']==3].재구매의향.values
# 연령2 : 3집단으로 줄임(요인분석)[in]
stats.f_oneway(anova1, anova2, anova3)
# pvalue=1.613686022426391e-25 < 0.05
# 세 집단 간 모두 차이가 있다 >> 사후 테스트 필요
[out]
F_onewayResult(statistic=72.42612494637737, pvalue=1.613686022426391e-25)연령별 집단과 재구매의향 사이의 평균값은 차이가 있다. 따라서 사후 테스트를 진행한다. p-value0.05 > p-vlaue 1.6136..e-25
[in]
# 연령에 따른 구매가격의 차이
anova1=df[df['연령2']==1].구매가격.values
anova2=df[df['연령2']==2].구매가격.values
anova3=df[df['연령2']==3].구매가격.values
stats.f_oneway(anova1, anova2, anova3)
# 세 집단간 차이가 있음
[out]
F_onewayResult(statistic=0.8181036982598708, pvalue=0.44245014422691564)세 집단과 차이가 없음 p-value 0.05 < p-value 0.4
...설명 필요 아무튼 안 해도 됨 평균값 차이가 없다고 보여진다...스킵
[in]
from statsmodels.stats.multicomp import pairwise_tukeyhsd
tukey = pairwise_tukeyhsd(endog=df['재구매의향'], # Data
groups=df['연령2'], # Groups
alpha=0.05) # Significance level 통계적 유의성
tukey.summary()
# 결과 해석
# 1-3, 2-3 집단 평균 차이 존재 : p-value: 0.001, reject : True
[out]
Multiple Comparison of Means - Tukey HSD,
FWER=0.05
group1 group2 meandiff p-adj lower upper reject
1 2 0.25 0.1275 -0.0526 0.5526 False
1 3 1.9905 0.001 1.5849 2.396 True
2 3 1.7405 0.001 1.3514 2.1295 True
투키 검정결과 1집단(10~20대 응답자)과 3집단(50대 이상 응답자), 그리고 2집단(30~40대 응답자)과 3집단 사이에 재구매의향에 차이가
있는 것으로 드러났다.
상관분석
독립변인과 종속변인이 모두 연속변인일 때, 서로 어느정도의 관련성이 있는가를 알아보기 위해 사용
상관관계에서는 어느것이 독립변인이고 종속변인인지 구분하는것은 애매하고,그냥 이 사이에 관련성이 있는가를 알 수 있을 뿐이다.
우리는 상관계수, 피어슨r 값으로 상관관계 검정을 할 것 이다.
r을 구하는 공식은 다음과 같다.
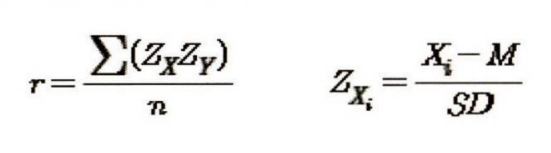
[in]
sp.stats.pearsonr(df['재구매의향'], df['구입조언']) #피어슨 상관관계 구하는거)
corr = sp.stats.pearsonr(df['재구매의향'], df['구입조언'])
print('correlation coefficient=%.3f, p-value=%.3f' %(corr))
df.corr(method='pearson')
#method='pearson' 옵션은 피어슨 상관 계수 계산 방법을 지정
[out]
correlation coefficient=0.418, p-value=0.000
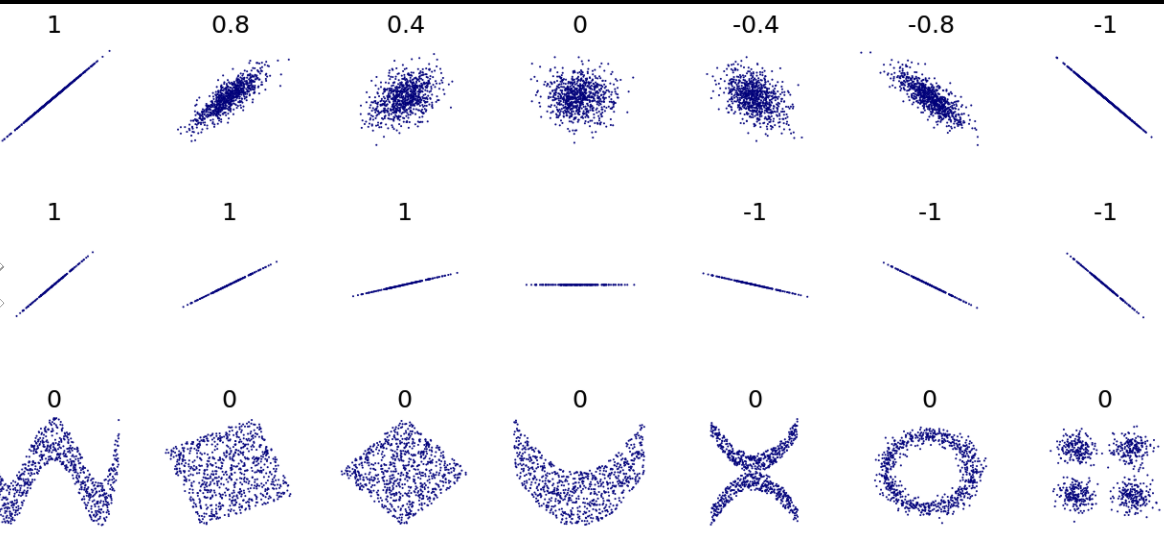
(correlation coefficient = 상관계수(점들이 얼마나 퍼져있는가 1은 완전 모여있는거 0은 완전 퍼져있는거)
0.41은 중간정도의 양의 상관관계이고 통계적으로 유의미 하다. 따라서 귀무가설을 기각함(p-value = 0)양의 상관계수 : /
음의 상관계수 : \
0의 상관계수 : ㅡ
숫자의 크기는 힘의 크기 : 점들이 얼마나 퍼져있는가- 1은 완전 모여있는거 0은 완전 퍼져있는거
각도는 상관 없지만 완전히 누워 수평을 이룬다면 0이 된다.
r은 -1과 1 사이의 값을 가지며, -1은 완전한 음의 상관 관계를 나타내며, 1은 완전한 양의 상관 관계를 나타냅니다. 0은 변수 간에 상관 관계가 없음을 나타냅니다.
(대체로 0.7이상이면 강한 상관관계, 0.3 이하이면 약한 상관관계로 본다.)
음의 상관관계는 반비례적 관계를 뜻 하며 양의 상관관계는 비례적 관계를 뜻 한다.
회귀분석
상관분석과 마찬가지로 독립변수와 종속변수가 모두 연속변인일 때 사용한다. 변인들이 불연속이라면 0과 1의 두 값을 가진 가변인으로 변환하여 연속변인인 척하여 분석한다.
상관분석은 두 변인의 관계성을 보는것이기 때문에 무엇이 종속변수고 독립변수인지 따지지 않지만 회귀분석은 하나 혹은 여러개의 변인이 특정값을 가질 때 그것과 관계있는 다른 변인의 값을 예측하고자 하기위해 회귀분석을 사용한다.
즉, 회귀분석은 하나 혹은 여러 독립변인이 하나의 종속변인에 어떤 영향을 미치는지 그 인과관계를 규명한다.
회귀분석의 목적은 종속 변수의 값을 예측하기 위해 독립 변수의 값을 사용하는 것입니다. 이는 기존의 데이터를 기반으로 독립 변수의 값을 입력하면 종속 변수의 값을 예측할 수 있는 모델을 만드는 것입니다. (인과관계를 모사한 분석기법)
시간적 선후관계가 없는 횡단면적 데이터(cross-sectional data)인 경우 인과관계를 주장하긴 어렵다.
상관계수가 클수록 회귀분석의 정확성이 높아집니다.
[in]
ols(formula='재구매의향 ~ 성별+연령+학력+월수입+사용기간+구매가격+구입조언+브랜드이미지+가격만족도+구매중요도1_메모리+하루사용시간', data=df).fit().summary()
#Ordinary Least Squares(일반적 최소제곱)란, 회귀분석에서 예측치와 실제 값의 차이(오차)의 제곱을 최소화하는 것을 목적으로 하는 회귀분석 방법
#재구매의향 = 종속변수
#성별+연령+학력+월수입+사용기간+구매가격+구입조언+브랜드이미지+가격만족도+구매중요도1_메모리+하루사용시간 = 독립변수
[out]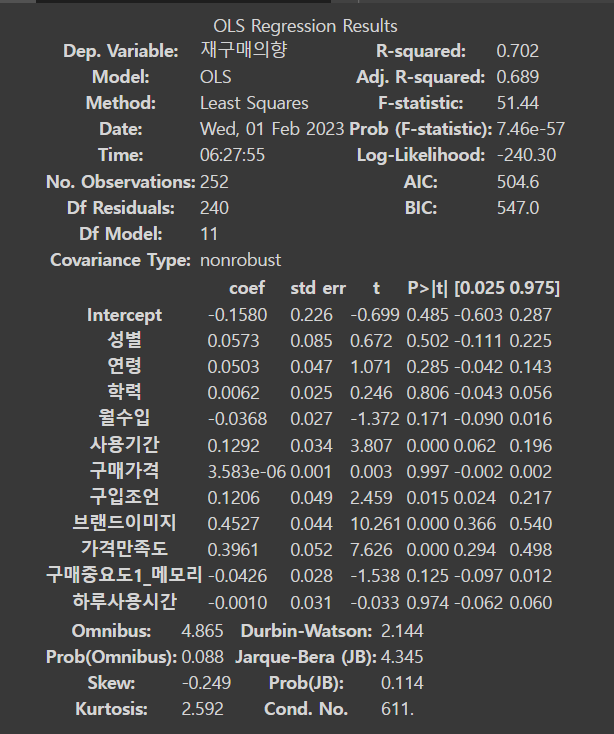
coef 열은 각 독립 변수와 종속 변수 사이의 계수 값을 나타낸다.
std err 열은 각 계수에 대한 표준 오차 값을 나타낸다.
t-value와 p-value는 각 계수의 통계적 유의성을 나타낸다.
(0.025, 0.975) 열은 각 계수에 대한 95% 신뢰 구간을 나타낸다.
회귀방정식에 투입된 11개의 독립변인 중에서 사용기간,구입
조언,브랜드이미지,가격만족도의 4가지 변인의 표준화 계수값
(coef 바이 각각 0.1292 (p=.000), 0.1206(p=.015), 0.4527(p=.000),0.3961 (p=.000)으로 종속변인인 구매의도에 통계적으로 유의미한 영향을 미친 것으로 나타났다.
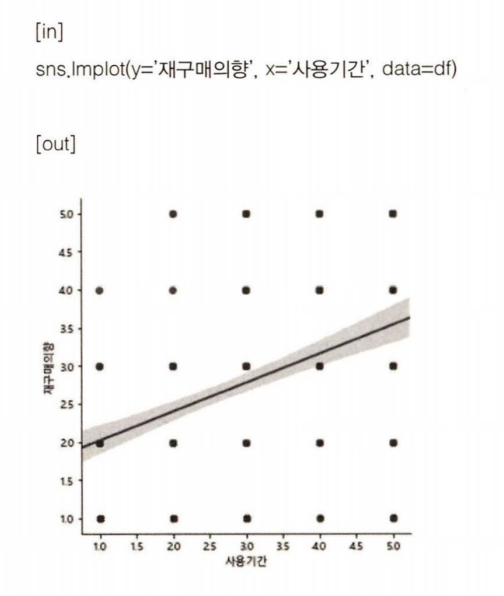
사용기간이 길 수록 재구매의향이 높아진다는 그래프
