[알고리즘] 다익스트라 알고리즘(Dijkstra Algorithm)

다익스트라 알고리즘

다익스트라 알고리즘은 최단거리를 구하는 알고리즘입니다. 다익스트라 알고리즘을 사용하면, 하나의 노드에서 다른 모든 노드까지의 거리를 구할 수 있습니다.

즉, 시작점에서 다른 모든 정점까지의 최단 경로의 길이를 찾는 알고리즘이다.

---

조건

다익스트라 알고리즘을 사용할 수 있는 몇가지 조건이 있다.

• 방향 그래프
• 0 이상 가중치여야 한다.
  • 음수 가중치가 있으면 안된다. ==> 음수가 있을 땐, 벨만 포드
    (이전까지 계산해둔 최소가 최소라고 보장할 수 없기 때문이다.)
• 사이클이 없어야 한다.
  위와 같은 조건들을 모두 충족해야만 다익스트라 알고리즘을 사용할 수 있다.

다익스트라 알고리즘은 일종의 길찾기 알고리즘이다.

---

아이디어

다익스트라의 기본적인 아이디어를 살펴보자.

• BFS가 베이스이다.
  BFS처럼 시작 정점에서 가까운 순서대로 방문하게 된다.
• 그리디 알고리즘
  매 순간 최단 거리 정점을 선택하므로 그리디 알고리즘 기반이다.

---

다익스트라 알고리즘 사용 예시

1. 출발 노드를 설정합니다.
2. 출발 노드를 기준으로 각 노드의 최소 비용을 저장합니다.
3. 방문하지 않은 노드 중에서 가장 비용이 적은 노드를 선택합니다.
4. 해당 노드를 거쳐서 특정한 노드로 가는 경우를 고려하여 최소 비용을 갱신합니다.
5. 위 과정에서 3번 ~ 4번을 반복합니다.
   

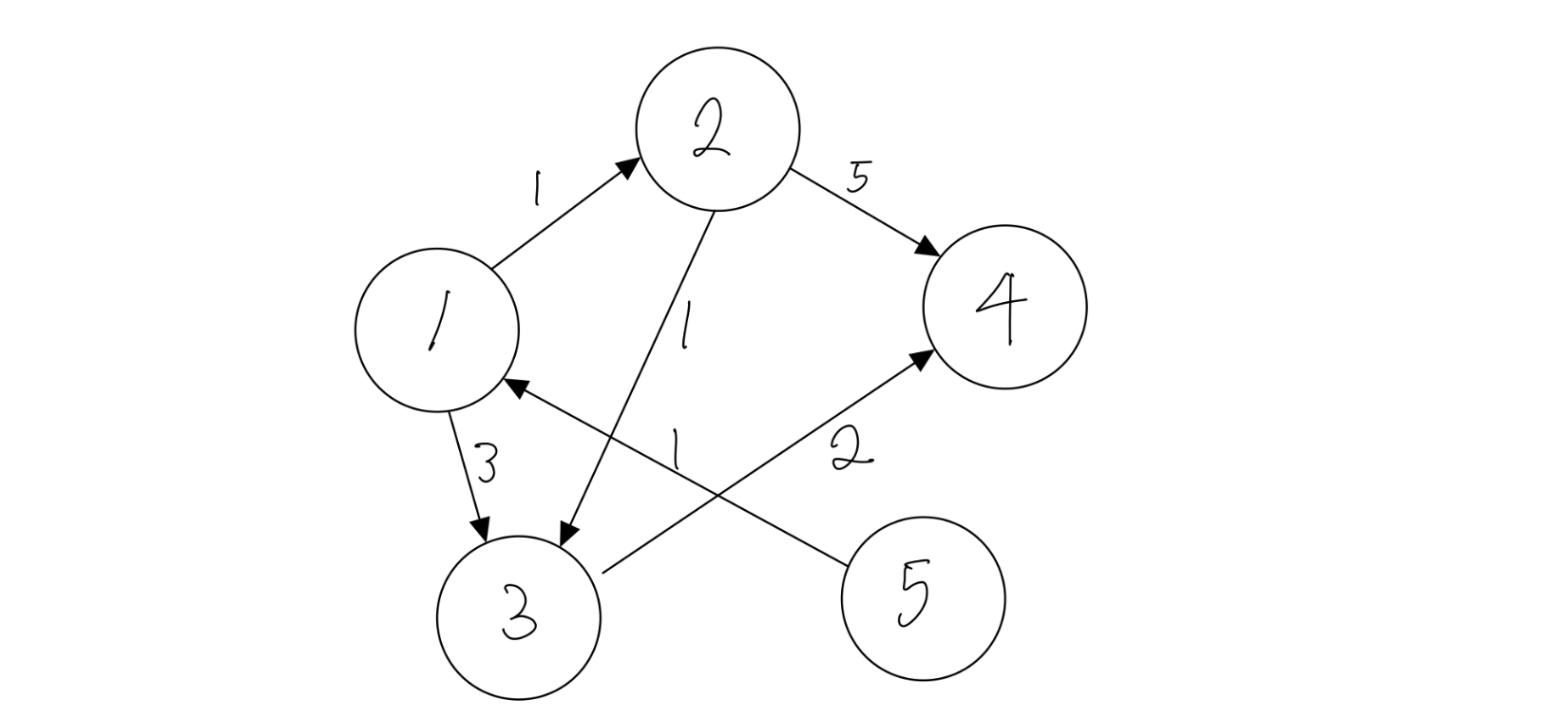
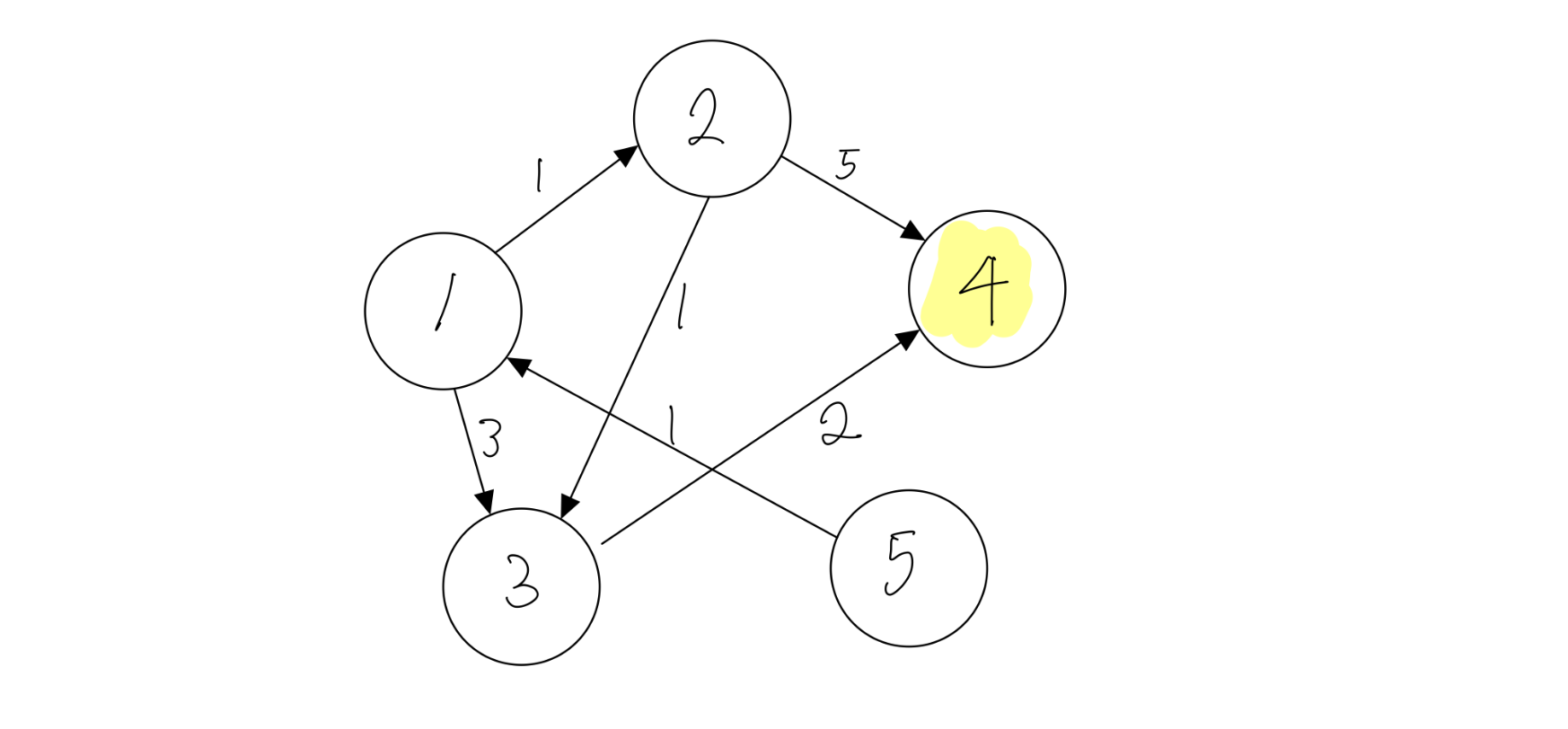
• 가중치 방향 그래프를 통해 다익스트라 알고리즘의 원리를 더 자세히 살펴 보겠습니다.

• 노드 1에서부터 다른 모든 노드까지의 최단 경로를 구해보겠습니다.

• 초기에는 모두 거리를 무한으로 설정합니다.

  거리	1	2	3	4	5
  x	INF	INF	INF	INF	INF

---

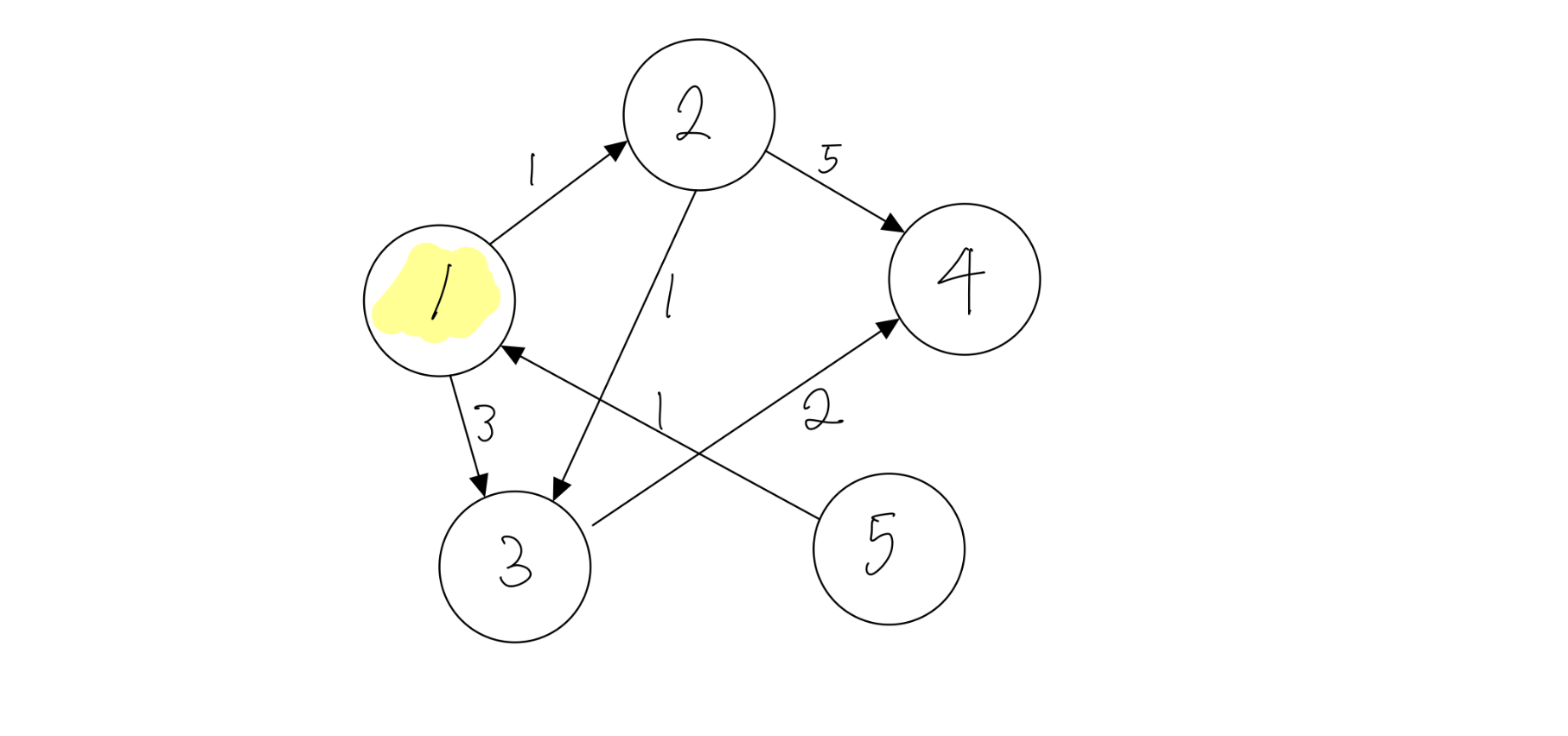
• 처음에는 자기 자신까지의 거리를 0으로 놓고 노드 1과 직접 연결된 노드까지의 거리를 입력합니다.

• 이제 1번 노드는 방문처리합니다.

  거리	1	2	3	4	5
  x	0	1	3	INF	INF

---

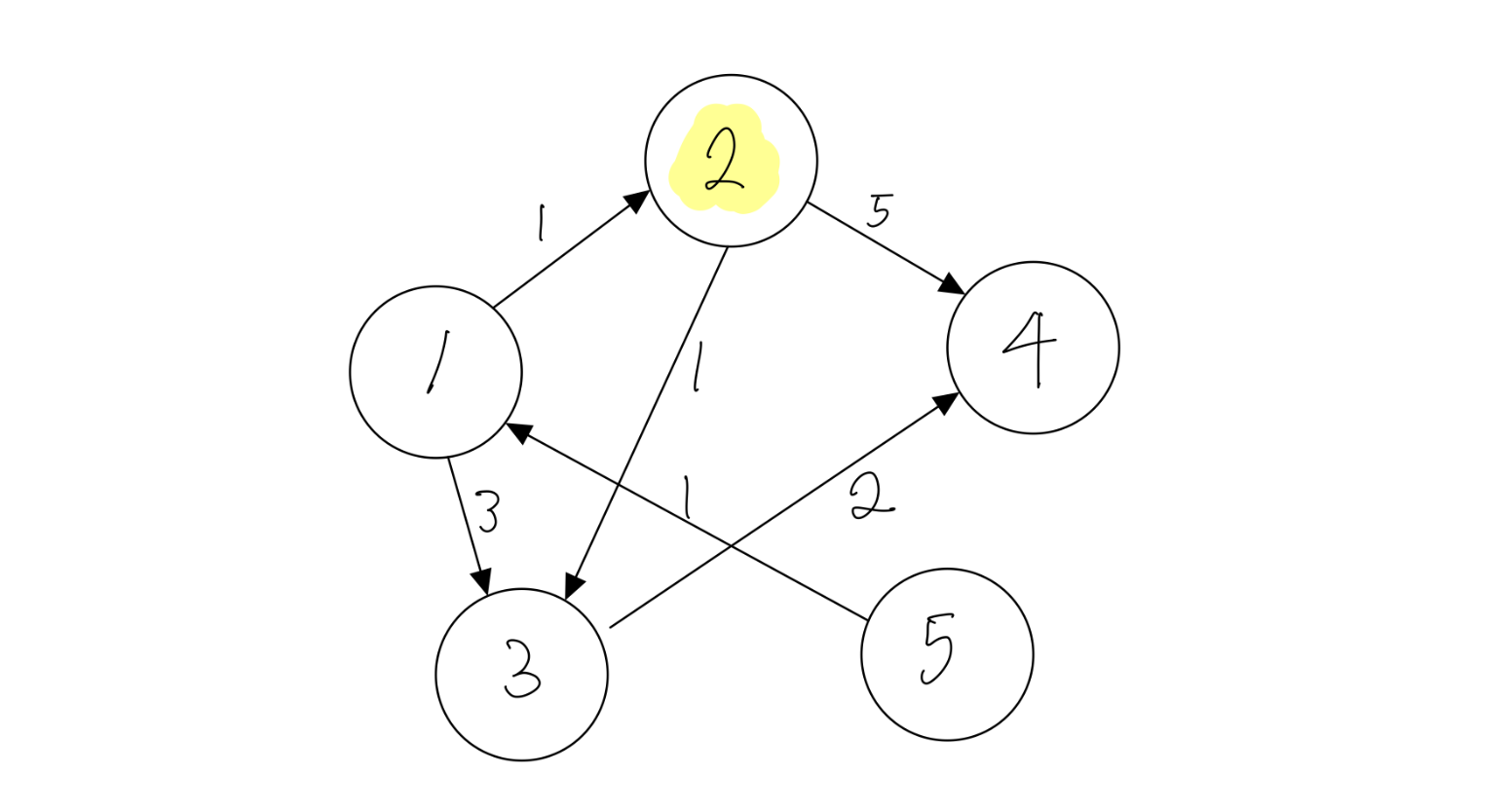
• 방문처리되지 않은 노드 중 입력된 거리가 가장 짧은 2번 노드를 선택합니다.

• 2를 기준으로 하였을 때 거리를 구하면, 3번 노드까지의 거리가 1 + 1로 2가 됩니다. 기존에 입력된 3보다 작으므로 값을 갱신합니다.

• 4번 까지의 거리는 1 + 5로 6이 됩니다.

• 이제 2번 노드는 방문처리합니다.

  거리	1	2	3	4	5
  x	0	1	2	6	INF

---

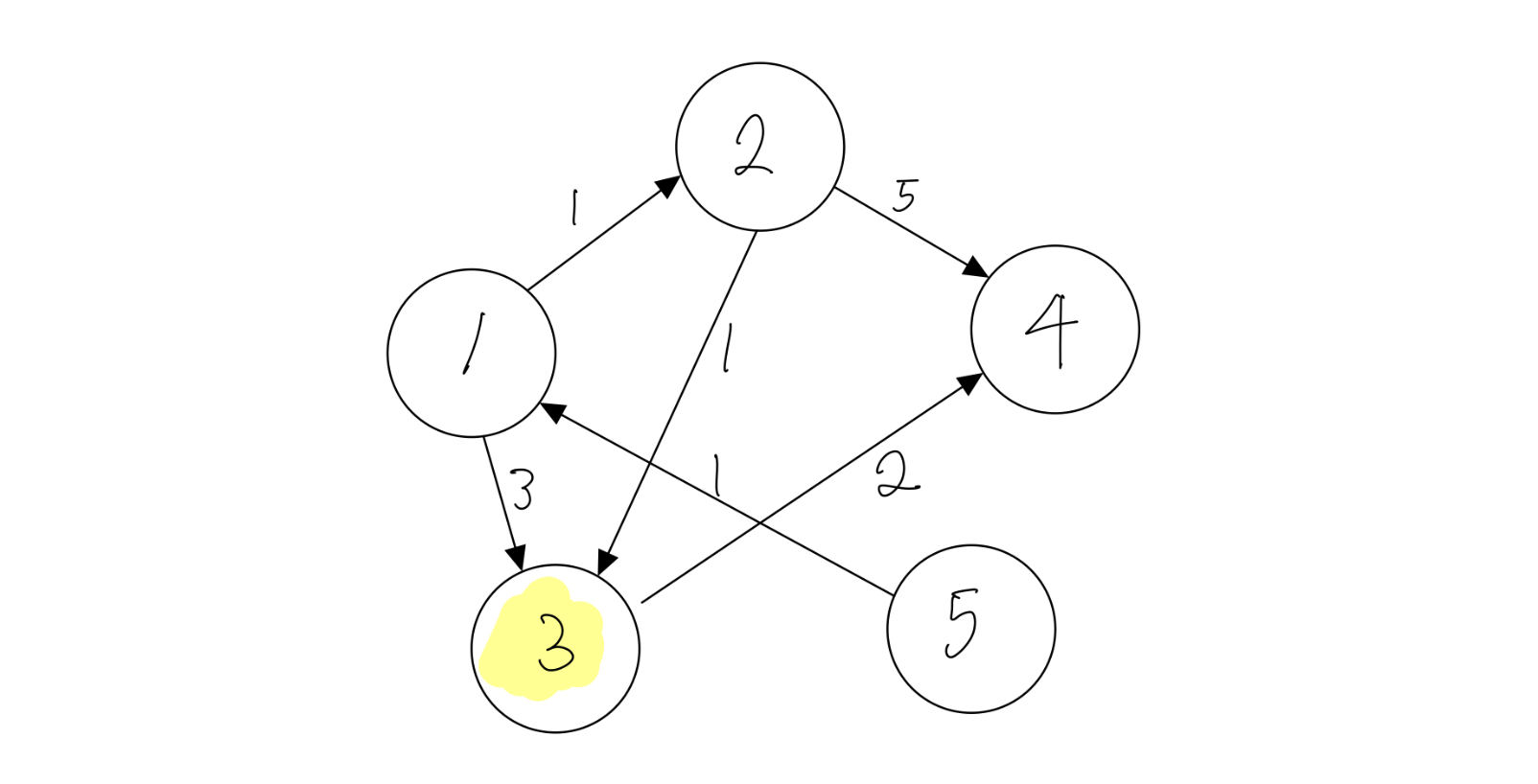
• 방문처리되지 않은 노드 중 입력된 거리가 가장 짧은 3번 노드를 선택합니다.

• 3번 노드를 기준으로 하였을 때, 4번 노드까지의 거리는 2 + 2로 4가 됩니다. - 기존에 입력된 6보다 작은 값이므로 값을 갱신합니다.

  거리	1	2	3	4	5
  x	0	1	2	4	INF

---

• 방문처리되지 않은 노드 중 입력된 거리가 가장 짧은 3번 노드를 선택합니다.

• 연결된 노드가 없으므로 최단거리 구하기를 마칩니다.

• 1번 노드로 부터 다른 모든 노드로부터의 최단거리는 아래의 표와 같습니다.

  거리	1	2	3	4	5
  x	0	1	2	4	INF

heap을 이용한 코드 구현 (Python)

import heapq
n, m = map(int, input().split())
k = int(input())                 # 시작할 노드
INF = int(1e9)

graph = [[] for _ in range(n+1)] 

distance = [INF] * (n+1)

for _ in range(m):
  u, v, w = map(int, input().split()) # u: 출발노드, v: 도착노드, w: 연결된 간선의 가중치 
  graph[u].append((v, w))             # 거리 정보와 도착노드를 같이 입력합니다

def dijkstra(start):
  q = []
  heapq.heappush(q, (0, start)) # 우선순위, 값 형태로 들어간다.
  distance[start] = 0

  while q:
    dist, now = heapq.heappop(q) # 우선순위가 가장 낮은 값(가장 작은 거리)이 나온다.
	# 현재 노드가 이미 처리된 적이 있는 노드라면 무시
    if distance[now] < dist: 
      continue               # 따라서 다음으로 넘어간다.
	# 현재 노드와 연결된 모든 노드 탐색
    for i in graph[now]:     
    # 현재 노드를 거쳐서, 다른 노드로 이동하는 거리가 더 짧은 경우
      if dist+i[1] < distance[i[0]]: 
        distance[i[0]] = dist+i[1]   #
        heapq.heappush(q, (dist+i[1], i[0]))
dijkstra(k)
print(distance)

참고 블로그

https://velog.io/@wonhee010/%EB%8B%A4%EC%9D%B5%EC%8A%A4%ED%8A%B8%EB%9D%BC-%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98Dijkstra-Algorithm
https://velog.io/@tks7205/%EB%8B%A4%EC%9D%B5%EC%8A%A4%ED%8A%B8%EB%9D%BC-%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98-with-python#heap%EC%9D%84-%ED%99%9C%EC%9A%A9%ED%95%9C-%EA%B5%AC%ED%98%84