[알고리즘] 비트마스크(BitMask)

이민우·2024년 4월 12일

CS 알고리즘

CS_알고리즘

목록 보기

15/15

비트마스크(BitMask)란?

비트마스크(BitMask)는 이진수를 사용하는 컴퓨터의 연산 방식을 이용하여, 정수의 이진수 표현을 자료 구조로 쓰는 기법을 말한다.
이진수는 0 또는 1을 이용하므로 하나의 비트(bit)가 표현할 수 있는 경우는 두 가지이다.
보통 어떤 비트가 1이면 "켜져 있다"라고 말하며, 0이면 "꺼져 있다"라고 말한다.

비트마스크의 장점

비트마스크는 크게 어려운 개념이 아니며, 이 개념을 알고 있다면 매우 유용한 경우가 꽤나 있다. 비트마스크의 장점들은 다음과 같다.

1. 수행 시간이 빠르다.

비트마스크 연산은 bit 연산이기 때문에 O(1)에 구현되는 것이 많다. 따라서 다른 자료구조를 이용하는 것보다 훨씬 빠르게 동작하게 된다.
다만, 비트마스크를 이용하는 경우에는 비트의 개수만큼 원소를 다룰 수 있기 때문에 연산 횟수가 적은 경우에는 속도에 큰 차이가 없지만, 연산 횟수가 늘어날수록 차이가 매우 커지게 된다.

2. 코드가 짧다.

다양한 집합 연산들을 비트연산자로 한 줄로 작성할 수 있기 때문에 반복문, 조건문 등을 이용한 코드보다 훨씬 간결한 코드를 작성할 수 있다.

3. 메모리 사용량이 더 적다.

개인적으로, 비트마스크를 이용하는 가장 큰 이유라고 생각한다.
간단한 예시로, bit가 10개인 경우에는 각 bit당 두 가지 경우를 $2^{10}$ 이기 때문에 가지의 경우를 10bit 이진수 하나로 표현이 가능하다.
이처럼 하나의 정수로 매우 많은 경우의 수를 표현할 수 있기 때문에 메모리 측면에서 효율적이며, 더 많은 데이터를 미리 계산해서 저장해 둘 수 있는 장점이 있다. (DP에 매우 유용하다)

비트 연산자

비트마스크를 이용하기 위해서, 정수 변수를 비트 별로 조작할 수 있는 비트연산자를 사용한다. 두 정수 변수 또는 하나의 정수 변수를 이용하여 새로운 값을 만들어 내는 것이 목적이다.

1. AND 연산

두 정수 변수 a와 b를 통해서 c를 생성한다고 가정하면, a와 b를 한 bit씩 비교하면서 해당 비트가 둘 다 켜져 있는 경우에만 c의 해당 비트를 켠다.
C에서 제공하는 연산자 기호는 ' & '이다.
(ex. c = a & b)

2. OR 연산

AND 연산과 같은 방식으로, 해당 비트가 둘 중 하나라도 켜져 있는 경우에 c의 해당 비트를 켠다.
C에서 제공하는 연산자 기호는 ' | ' 이다.
(ex. c = a | b)

3. XOR 연산

마찬가지로 같은 방식이며, 해당 비트가 둘 중 하나만 켜져 있는 경우에 c의 해당 비트를 켠다.
C에서 제공하는 연산자 기호는 ' ^ ' 이다.
(ex. c = a ^ b)

4. NOT 연산

정수 하나를 입력받아서 켜져 있는 비트는 끄고, 꺼져 있는 비트는 켠 결과를 반환한다.
C에서 제공하는 연산자 기호는 ' ~ ' 이다.
(ex. c = ~a)

5. 시프트(shift) 연산

시프트 연산자는 정수 a의 비트들을 왼쪽 또는 오른쪽으로 원하는 만큼 움직인다. 움직이고 나서 빈자리는 0으로 채워지게 된다. 예를 들어 13 (1101)을 오른쪽으로 1bit 움직인다고 하면, 6 (0110)이 되는 것이다.
연산자 기호는 ' << ' 또는 ' >> ' 이다.
(ex. c = (a << 1) )

아래는 실제 예시이다.

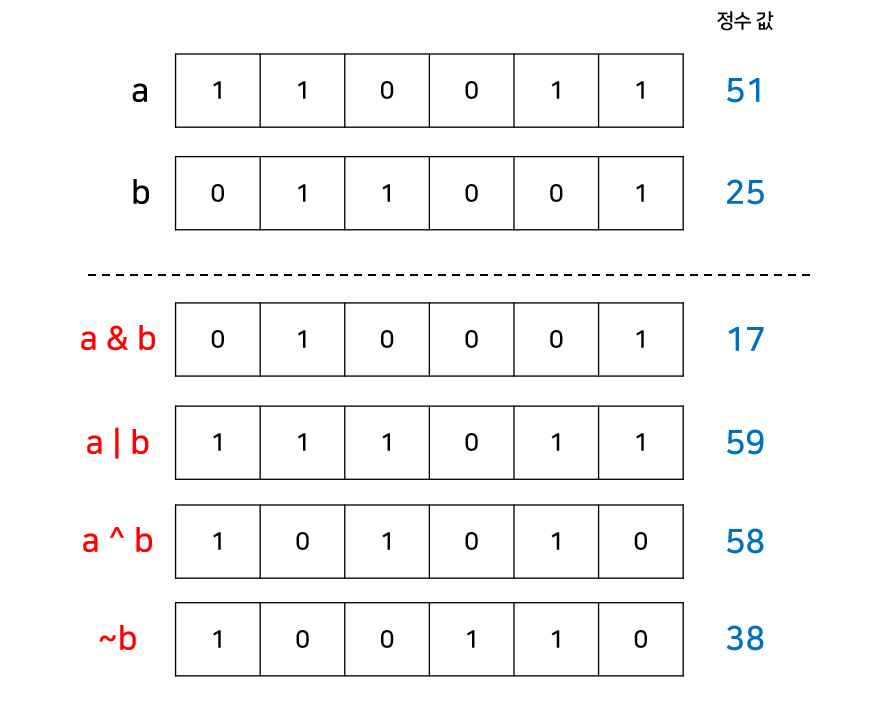
비트 연산 활용

원소 추가

현재 이진수로 10101로 표현되고 있을 때, i번째 비트 값을 1로 변경하려고 한다.
i = 3일 때 변경 후에는 11101이 나와야 한다. 이때는 OR연산을 활용한다
```
10101 | 1 << 3
```

원소 삭제

반대로 0으로 변경하려면, AND연산과 NOT 연산을 활용한다.
```
11101 & ~1 << 3
```

원소 조회

i번째 비트가 무슨 값인지 알려면, AND연산을** 활용한다.

10101 & 1 << i

3번째 비트 값 : 10101 & (1 << 3) = 10101 & 01000 → 0
4번째 비트 값 : 10101 & (1 << 4) = 10101 & 10000 → 10000

이처럼 결과값이 0이 나왔을 때는 i번째 비트 값이 0인 것을 파악할 수 있다. (반대로 0이 아니면 무조건 1인 것)

집합 연산

비트마스킹을 이용하면 원소를 추가, 삭제, 토글 하는 연산 외에도 합집합, 교집합, 차집합 등등을 쉽게 구할 수 있습니다.

A | B   # 합집합
A & B   # 교집합
A & ~B  # 차집합 (A - B)
A ^ B   # A와 B 중 하나에만 포함된 원소들의 집합

집합의 크기

집합의 크기를 구하기 위해선, 비트에서 1인 비트 수를 세주면 된다. 이는 재귀 함수로 구현할 수 있다. x % 2는 마지막 비트를 의미, x // 2는 마지막 비트의 삭제를 의미한다.

def bitCount(x):
	if x == 0: return 0
	return x % 2 + bitCount(x//2)

참고 블로그

https://github.com/gyoogle/tech-interview-for-developer/blob/master/Algorithm/%EB%B9%84%ED%8A%B8%EB%A7%88%EC%8A%A4%ED%81%AC(BitMask).md
https://velog.io/@1998yuki0331/Python-%EB%B9%84%ED%8A%B8-%EB%A7%88%EC%8A%A4%ED%82%B9-%EC%A0%95%EB%A6%AC

이민우

백엔드 공부중입니다!

이전 포스트