[자료구조] 배열과 리스트, 스택과 큐

자료구조

[목차]

• Array
• Linked List
• Stack and Queue

코드 구현은 Python 기준입니다!

Array

가장 기본적인 자료구조인 Array 자료구조는, 논리적 저장 순서와 물리적 저장 순서가 일치한다. 가장 큰 특징은 순차적으로 데이터를 저장한다는 점입니다.(연속적이다)
따라서 인덱스(index)로 해당 원소(element)에 접근할 수 있다. 그렇기 때문에 찾고자 하는 원소의 인덱스 값을 알고 있으면 Big-O(1)에 해당 원소로 접근할 수 있다. 즉 random access 가 가능하다는 장점이 있는 것이다.

💡 문제점

하지만 삭제 또는 삽입의 과정에서는 해당 원소에 접근하여 작업을 완료한 뒤(O(1)), 또 한 가지의 작업을 추가적으로 해줘야 하기 때문에, 시간이 더 걸린다. 만약 배열의 원소 중 어느 원소를 삭제했다고 했을 때, 배열의 연속적인 특징이 깨지게 된다. 즉 빈 공간이 생기는 것이다. 따라서 삭제한 원소보다 큰 인덱스를 갖는 원소들을 shift해줘야 하는 비용(cost)이 발생하고 이 경우의 시간 복잡도는 O(n)가 된다. 그렇기 때문에 Array 자료구조에서 삭제 기능에 대한 time complexity 의 worst case 는 O(n)이 된다.

삽입의 경우도 마찬가지이다. 만약 첫번째 자리에 새로운 원소를 추가하고자 한다면 모든 원소들의 인덱스를 1 씩 shift 해줘야 하므로 이 경우도 O(n)의 시간을 요구하게 된다.

💡 Array를 적용시키면 좋을 데이터의 예를 구체적으로 들어주세요.

Linked List(동적 자료 구조)

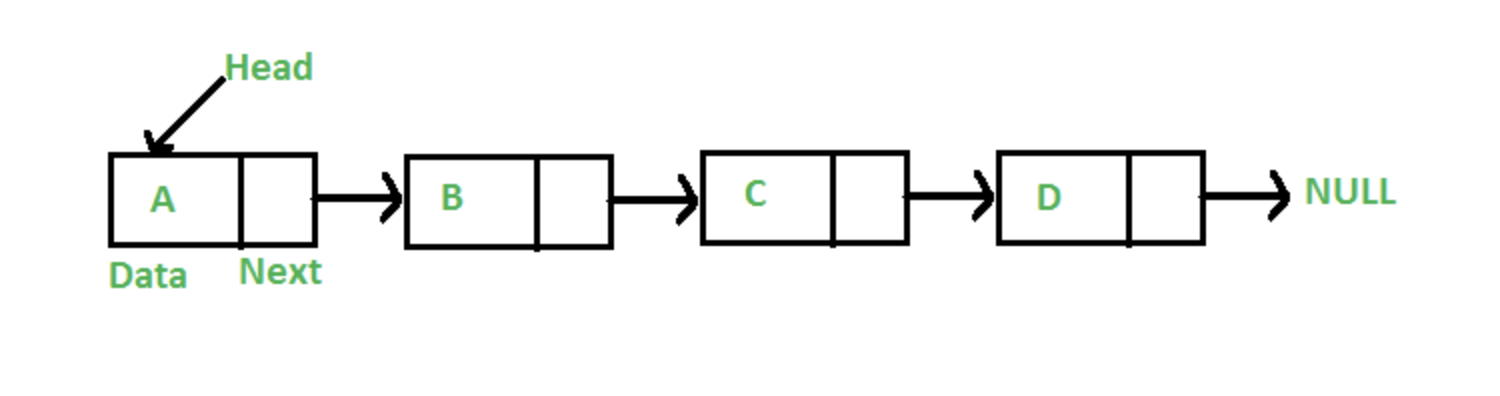
https://github.com/gyoogle/tech-interview-for-developer/blob/master/Computer%20Science/Data%20Structure/Linked%20List.md

특징

• 연속적인 메모리 위치에 저장되지 않는 선형 데이터 구조(포인터를 사용해서 연결된다)

• 각 노드는 데이터 필드와 다음 노드에 대한 참조를 포함하는 노드로 구성

사용하는 이유

배열은 비슷한 유형의 선형 데이터를 저장하는데 사용할 수 있지만 제한 사항이 있음

배열의 크기가 고정되어 있어 미리 요소의 수에 대해 할당을 받아야 함

새로운 요소를 삽입하는 것은 비용이 많이 듬 (공간을 만들고, 기존 요소 전부 이동)

위에서 배열에 대한 문제점을 해결하기 위한 자료구조가 linked list 이다. 각각의 원소들은 자기 자신 다음에 어떤 원소인지만을 기억하고 있다. 따라서 이 부분만 다른 값으로 바꿔주면 삭제와 삽입을 O(1) 만에 해결할 수 있는 것이다.

하지만 Linked List 역시 한 가지 문제가 있다. 원하는 위치에 삽입을 하고자 하면 원하는 위치를 Search 과정에 있어서 첫번째 원소부터 다 확인해봐야 한다는 것이다. Array 와는 달리 논리적 저장 순서와 물리적 저장 순서가 일치하지 않기 때문이다. 이것은 일단 삽입하고 정렬하는 것과 마찬가지이다. 이 과정 때문에, 어떠한 원소를 삭제 또는 추가하고자 했을 때, 그 원소를 찾기 위해서 O(n)의 시간이 추가적으로 발생하게 된다.

결국 linked list 자료구조는 search 에도 O(n)의 time complexity 를 갖고, 삽입, 삭제에 대해서도 O(n)의 time complexity 를 갖는다. 그렇다고 해서 아주 쓸모없는 자료구조는 아니기에, 우리가 학습하는 것이다. 이 Linked List 는 Tree 구조의 근간이 되는 자료구조이며, Tree 에서 사용되었을 때 그 유용성이 드러난다

📌 Array vs Linked List 정리

Array는 인덱스(index)로 해당 원소(element)에 접근할 수 있어 찾고자 하는 원소의 인덱스 값을 알고 있으면 O(1)에 해당 원소로 접근할 수 있습니다. 즉, RandomAccess가 가능해 속도가 빠르다는 장점이 있습니다.하지만 삽입 또는 삭제의 과정에서 각 원소들을 shift 해줘야 하는 비용이 생겨 이 경우 시간 복잡도는 O(n)이 된다는 단점이 있습니다.

이 문제점을 해결하기 위한 자료구조가 linkedlist입니다. 각각의 원소들은 자기 자신 다음에 어떤 원소인지만을 기억하고 있기 때문에 이 부분만 다른 값으로 바꿔주면 삽입과 삭제를 O(1)로 해결할 수 있습니다. 하지만 LinkedList는 원하는 위치에 한 번에 접근할 수 없다는 단점이 있습니다. 원하는 위치에 삽입을 하고자 하면 원하는 위치를 Search 과정에 있어서 첫번째 원소부터 다 확인해봐야 합니다.

간단히 정리하면,
Array는 검색이 빠르지만, 삽입, 삭제가 느리다.
LinkedList는 삽입, 삭제가 빠르지만, 검색이 느리다.

🔎 추가로 알면 좋은 내용

그럼 위에서 말한 linked list에서 검색 속도에 대해 단점을 보완한 자료구조가 있을까??

⭐️ skip list

skip list는 linked list와 비슷하게 다음 원소를 가리키는 포인터를 가지고 있다.

그렇기 때문에 데이터의 삽입/삭제를 빠르게 할 수 있다. 이것은 linked list 특성상 당연해 보이는데 skip list는 여기에 검색 속도까지 책임진다.

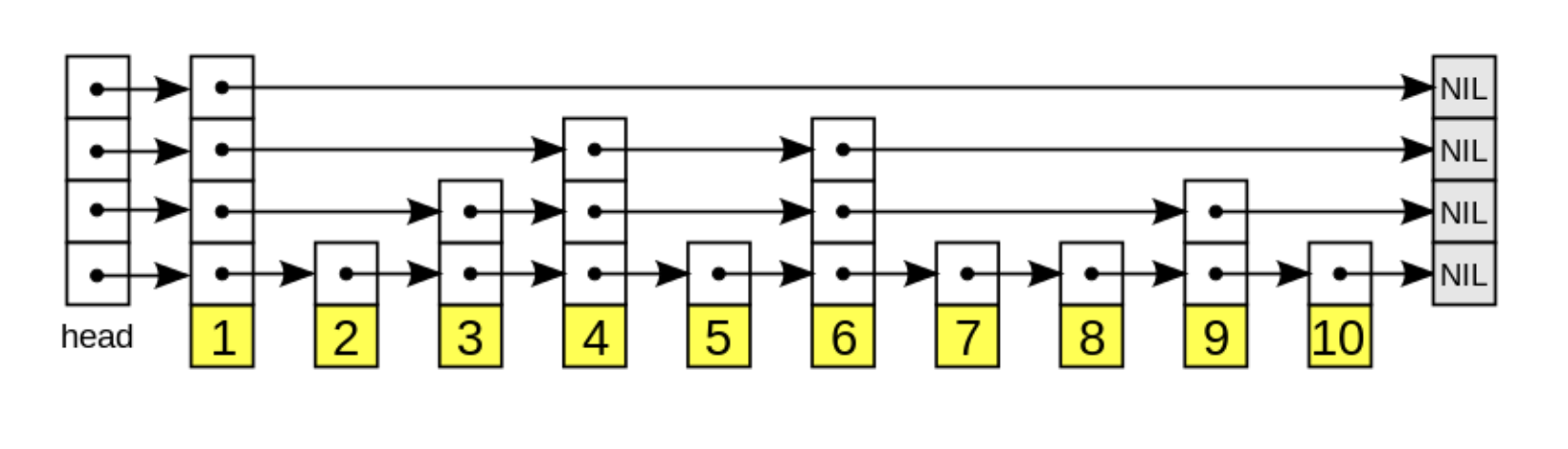
특징

• 이진 검색 트리를 간단하게 구현하면서도 검색, 삽입, 삭제 연산을 O(log n)의 시간 복잡도로 수행할 수 있는 자료구조입니다
• 확률적인 구성: 원소를 확률적으로 여러 레벨에 배치하여 구성합니다. 이를 통해 삽입, 삭제, 검색 연산이 O(log n)의 시간 복잡도를 가질 수 있습니다.
• 레벨이 높을수록 더 높은 확률로 건너뛰어지는 원소가 많아지기 때문에, 원소를 찾는 데에는 이진 검색과 유사한 방식으로 빠르게 탐색
• 단점으로는 구현 복잡성 및 레벨의 수가 많을수록 추가적인 메모리를 요구합니다

Stack and Queue

Stack

선형 자료구조의 일종으로 Last In First Out (LIFO) - 나중에 들어간 원소가 먼저 나온다. 또는 First In Last Out (FILO) - 먼저 들어간 원소가 나중에 나온다. 이것은 Stack 의 가장 큰 특징이다. 차곡차곡 쌓이는 구조로 먼저 Stack 에 들어가게 된 원소는 맨 바닥에 깔리게 된다. 그렇기 때문에 늦게 들어간 녀석들은 그 위에 쌓이게 되고 호출 시 가장 위에 있는 녀석이 호출되는 구조이다.

Queue

선형 자료구조의 일종으로 First In First Out (FIFO). 즉, 먼저 들어간 놈이 먼저 나온다. Stack 과는 반대로 먼저 들어간 놈이 맨 앞에서 대기하고 있다가 먼저 나오게 되는 구조이다. 참고로 Java Collection 에서 Queue 는 인터페이스이다. 이를 구현하고 있는 Priority queue등을 사용할 수 있다.

💡 Stack과 Queue의 실사용 예를 들어 간단히 설명해주세요.

✅ Python에서 일반적인 queue 구현

• collections 모듈의 deque(덱) 사용

queue 선언

from collections import deque
dq=deque()

원소 삭제

from collections import deque
dq=deque()

dq.pop() # 가장 뒤에 있는 원소
dq.popleft() # 가장 앞에 있는 원소

원소 삽입

dq.appendleft() # 가장 앞에 원소 삽입
de.append() # 가장 뒤에 원소 삽입

deque 회전 시키기

• rotate(n): 덱의 n만큼 회전(양수일 경우 오른쪽, 음수일 경우 왼쪽)

from collections import deque

a=[1,2,3,4,5]

dq_right=deque(a)
dq_left=deque(a)

dq_right.rotate(1) # n이 양수이면 오른쪽 회전
dq_left.rotate(-1) # n이 음수이면 왼쪽 회전

print(dq_right) # output ==> deque([5, 1, 2, 3, 4])
print(dq_left) # output ==> deque([2, 3, 4, 5, 1])

참고

https://github.com/gyoogle/tech-interview-for-developerhttps://github.com/JaeYeopHan/Interview_Question_for_Beginner/tree/main?tab=readme-ov-file
https://en.wikipedia.org/wiki/Skip_list