[자료구조] 힙, 트리

목차

• Heap
• Tree

Heap

[들어가기 전 ]

힙은, 우선순위 큐를 위해 만들어진 자료구조다.
먼저 우선순위 큐에 대해서 간략히 알아보자

우선순위 큐 : 우선순위의 개념을 큐에 도입한 자료구조

	데이터들이 우선순위를 가지고 있음. 우선순위가 높은 데이터가 먼저 나감

스택은 LIFO, 큐는 FIFO

Heap은 언제 사용할까?

• 시뮬레이션 시스템, 작업 스케줄링, 수치해석 계산
  우선순위 큐는 배열, 연결리스트, 힙으로 구현 (힙으로 구현이 가장 효율적!)

  우선순위 큐를 구현하는 표현 방법	삽입	삭제
  순서 없는 배열	O(1)	O(n)
  순서 없는 연결리스트	O(1)	O(n)
  정렬된 배열	O(n)	O(1)
  정렬된 연결 리스트	O(n)	O(1)
  힙	O(logn)	O(logn)

Heap이란?

• 완전 이진 트리의 일종
  • 여러 값 중, 최대값과 최소값을 빠르게 찾아내도록 만들어진 자료구조
    반정렬 상태
• 힙 트리는 중복된 값 허용 (이진 탐색 트리는 중복값 허용X)
• 힙은 일종의 반정렬 상태(느슨한 정렬 상태) 를 유지한다.
  • 큰 값이 상위 레벨에 있고 작은 값이 하위 레벨에 있다는 정도
    간단히 말하면 부모 노드의 키 값이 자식 노드의 키 값보다 항상 큰(작은) 이진 트리를 말한다.

힙(heap)의 종류

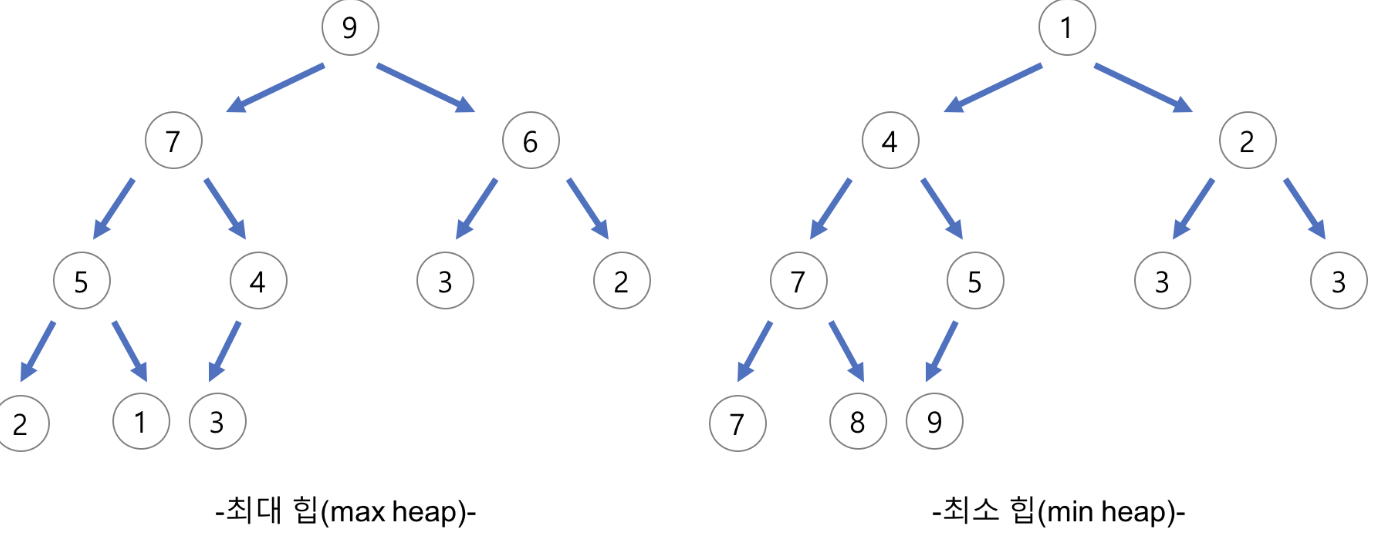
최대 힙

부모 노드의 키 값이 자식 노드의 키 값보다 크거나 같은 완전 이진 트리

최소 힙

부모 노드의 키 값이 자식 노드의 키 값보다 작거나 같은 완전 이진 트리

구현

📌 파이썬에 있는 heapq 모듈의 기능을 이용해 구현 하겠습니다

최소 힙 구현

파이썬의 힙은 기본적으로 최소 힙으로 구성되어 있습니다.

import heapq

hq=[]

heapq.heappush(hq, 3)
heapq.heappush(hq, 10)
heapq.heappush(hq, 1)
heapq.heappush(hq, 0)
heapq.heappush(hq, 4)

# 값을 삭제할떄는
heapq.heappop(hq)

## 리스트를 힙으로 변환
hq=[9, 20, 1, 8, 5, 0]
heapq.heapify(hq)

heappush 됐을 떄 기준으로 트리로 그려보면 다음과 같다.

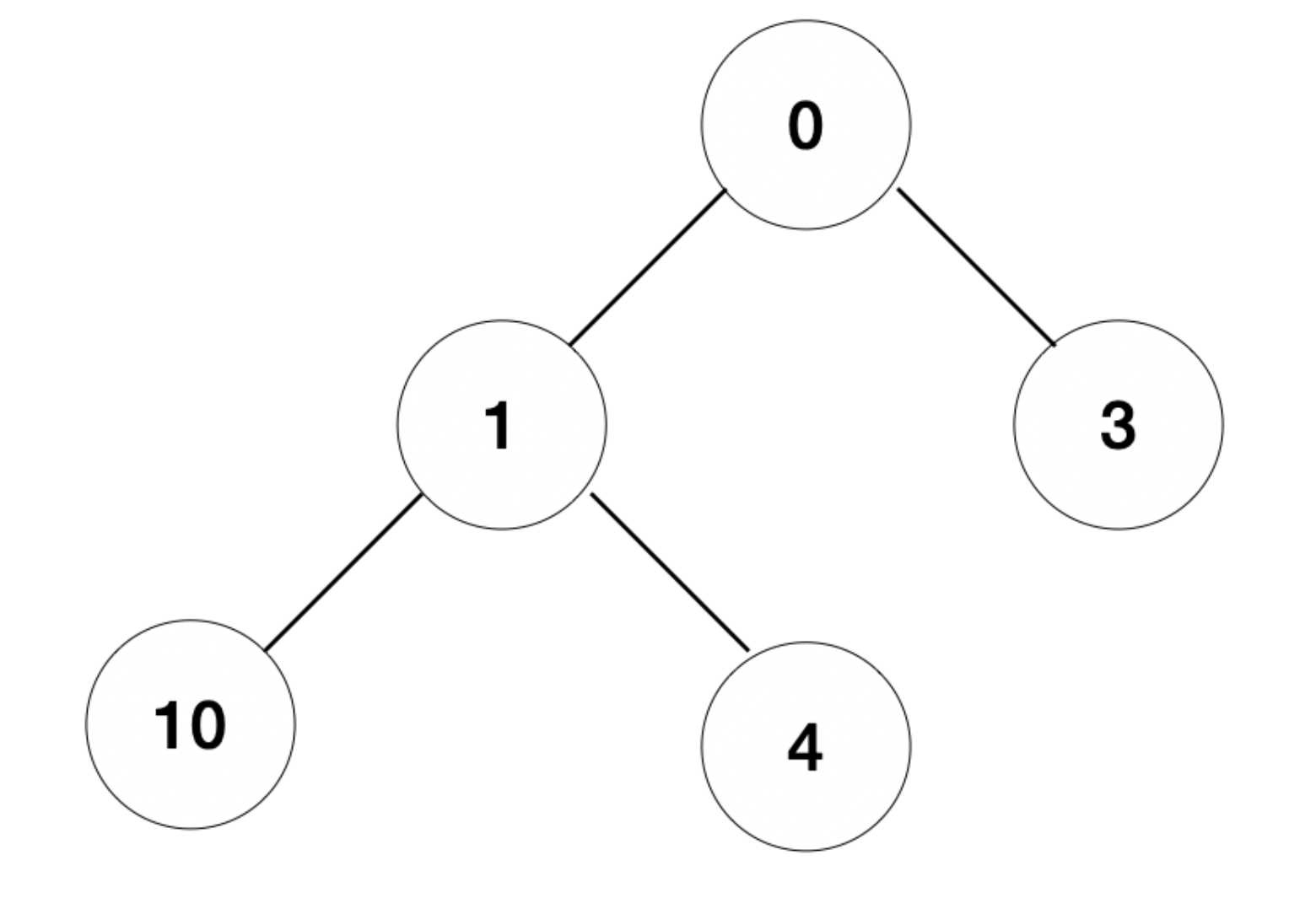
최대 힙 구현

처음 언급했듯, 파이썬의 heapq 라이브러리는 최소힙으로 구현되어있다. 하지만, 만약 이를 최대힙 즉, 가장 큰 수에 제일 높은 우선순위를 부여하고 싶다면 간단히 해당 수에 -1을 곱해 음수로 만들어주면 된다. 이후, pop할 때 다시 -1를 곱해 원래대로 양수로 만들어주면 최소힙을 최대힙으로 만들어 사용할 수 있다.

import heapq

hq=[]
# 음수로 만들어주기
heapq.heappush(hq, -3)
heapq.heappush(hq, -10)
heapq.heappush(hq, -1)
heapq.heappush(hq, -0)
heapq.heappush(hq, -4)

Tree

Node와 Edge로 이루어진 자료구조
Tree의 특성을 이해하자

트리는 스택이나 큐와 같은 선형 구조가 아닌 비선형 자료구조이다. 트리는 계층적 관계(Hierarchical Relationship)을 표현하는 자료구조이다. 이 트리라는 자료구조는 표현에 집중한다. 무엇인가를 저장하고 꺼내야 한다는 사고에서 벗어나 트리라는 자료구조를 바라보자.

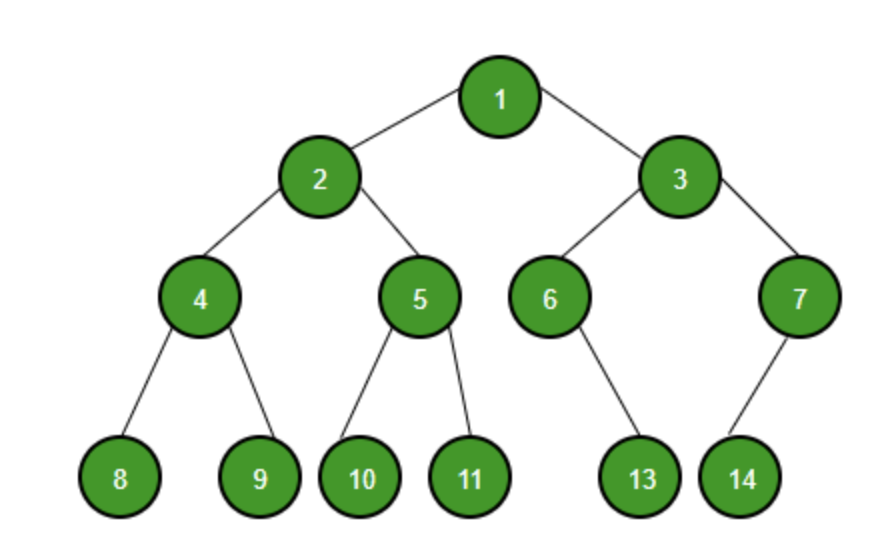
트리를 구성하고 있는 구성요소들(용어)

• Node (노드) : 트리를 구성하고 있는 각각의 요소를 의미한다.
• Edge (간선) : 트리를 구성하기 위해 노드와 노드를 연결하는 선을 의미한다.
• Root Node (루트 노드) : 트리 구조에서 최상위에 있는 노드를 의미한다.
• Terminal Node ( = leaf Node, 단말 노드) : 하위에 다른 노드가 연결되어 있지 않은 노드를 의미한다.
• Internal Node (내부노드, 비단말 노드) : 단말 노드를 제외한 모든 노드로 루트 노드를 포함한다.

트리의 특징

트리에는 사이클이 존재할 수 없다. (만약 사이클이 만들어진다면, 그것은 트리가 아니고 그래프다)
모든 노드는 자료형으로 표현이 가능하다.
루트에서 한 노드로 가는 경로는 유일한 경로 뿐이다.
노드의 개수가 N개면, 간선은 N-1개를 가진다

가장 중요한 것은, 그래프와 트리의 차이가 무엇인가인데, 이는 사이클의 유무로 설명할 수 있습니다.

트리 순회 방식

1. 전위 순회(pre-order)
   각 루트(Root)를 순차적으로 먼저 방문하는 방식

   (root-> Left -> Right)

2. 중위 순회(in-order)
   왼쪽 하위 트리를 방문 후 Root를 방문하는 방식

   (Left-> root -> Right)

3. 후위 순회(post-order)
   왼쪽 하위 트리부터 하위를 모두 방문 후 루트(Root)를 방문하는 방식

   (Left → Right → root)

4. 레벨 순회(level-order)
   루트(Root)부터 계층 별로 방문하는 방식이다.

참고

https://gyoogle.dev/blog/computer-science/data-structure/Heap.html
https://gmlwjd9405.github.io/2018/05/10/data-structure-heap.html