[BOJ] 11000 강의실배정.java

민지·2024년 7월 27일

Algorithm-Solution

목록 보기

8/12

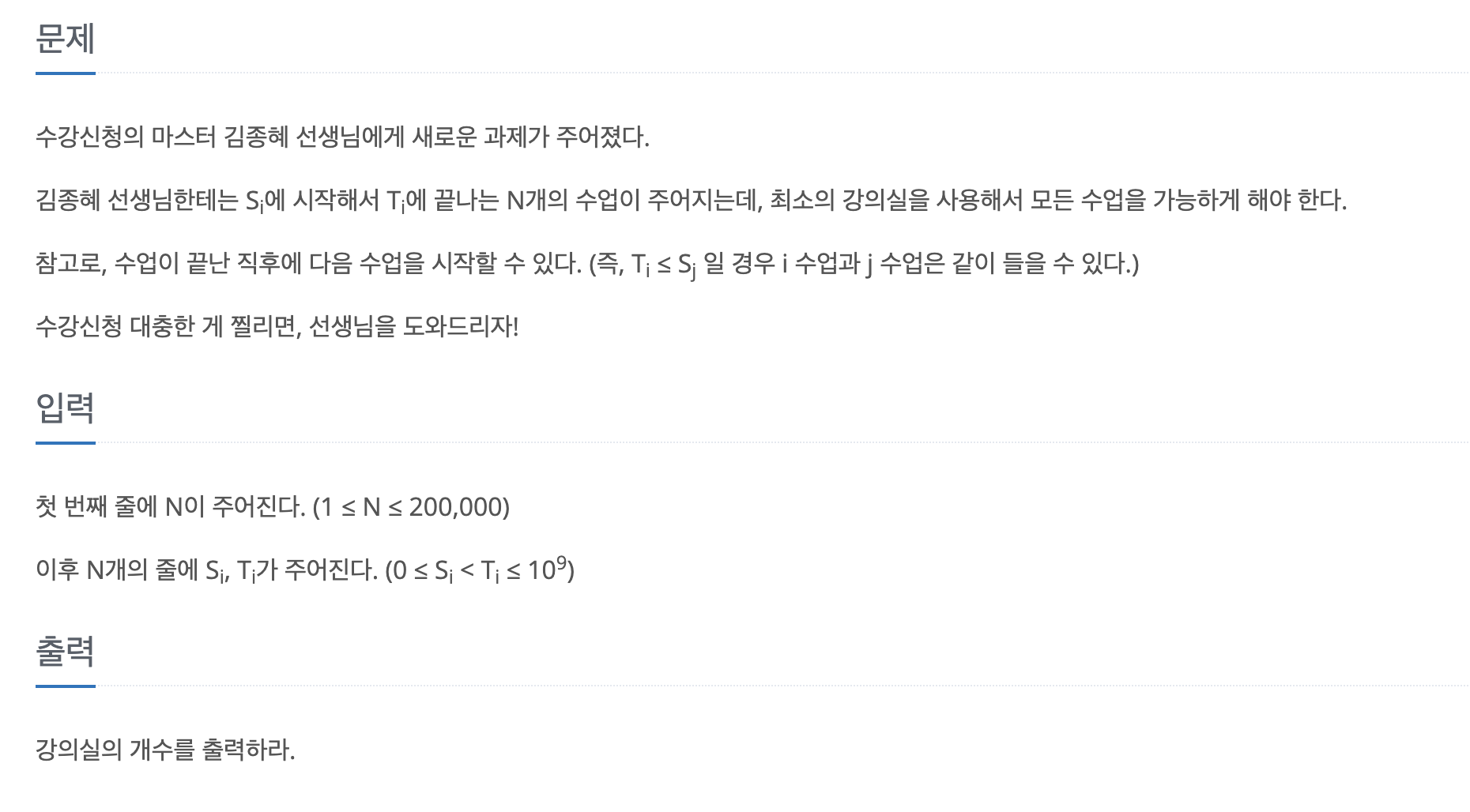
문제

백준 강의실배정

접근 방법

입력값에 따라 정렬을 사용해서 최적으로 비교할 방법을 찾아야겠다고 생각함.

어떤 기준으로 정렬할 것인가?

종료 시점이 중요하다고 생각했다. 그래서 종료 시점을 내림차순을 하기로 떠올림.

첫번째 시도: 정렬, 이중 반복문 탐색 (시간초과)

1. 종료 시점 내림차순, 시작 시점 오름차순

종료 시점이 큰 것부터 채워나가야 한다고 생각했다.
그리고 현재 강의 끝시간이 이미 있는 강의들의 시작시간보다 작거나 같으면 그 강의실에 넣고, 없으면 새로 강의실을 배정하도록 구현했다.

입력값이 200,000까지 있어서 강의실 체크하는 이중 반복문이 최악의 경우 시간초과가 날 수 있다.

시간초과 났다.

코드

package solution;

import java.util.*;
import java.io.*;

public class BOJ11000_강의실배정 {
    static class Lecture implements Comparable<Lecture> {
        int s;
        int e;

        Lecture(int s, int e) {
            this.s = s;
            this.e = e;
        }

        @Override
        public int compareTo(Lecture o) {
            if(this.e == o.e) return this.s - o.s;
            return o.e - this.e;
        }
    }
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st;
        int N = Integer.parseInt(br.readLine());
        Lecture[] lectures = new Lecture[N];
        for (int i = 0; i < N; i++) {
            st = new StringTokenizer(br.readLine());
            lectures[i] = new Lecture(Integer.parseInt(st.nextToken()), Integer.parseInt(st.nextToken()));
        }
        Arrays.sort(lectures);

        List<Lecture> lectureRooms = new ArrayList<>();
        for (int i = 0; i < N; i++) {
            Lecture now = lectures[i];
            boolean isIncluded = false;
            for (Lecture next : lectureRooms) {
                if(now.e <= next.s) {
                    next.s = now.s;
                    isIncluded = true;
                    break;
                }
            }
            if(!isIncluded) {
                lectureRooms.add(now);
            }
        }
        System.out.println(lectureRooms.size());
    }
}

결과

두번째: 정렬 + 우선순위큐 (통과)

순회하는 동안 어떤 자료구조에서 꺼내서 하나만 비교해도 어떻게 처리할지 결정되어야 시간초과를 벗어날 수 있다고 생각했다.

여기서 떠올려야할 자료구조는?

❗️우선순위 큐다.

이전 포스팅에서 우선순위큐를 떠올려야 하는 상황을 어떤 지점에서의 최댓값, 혹은 최솟값을 구해야 하는 상황이라고 했다.

여기서도 우선순위큐를 사용함으로서 비교를 최적화할 수 있다.

가정: 종료 시각을 기준으로 한다.

1. 우선순위큐: 현재 비교할 값을 시작값이 가장 큰 값이 나오도록 한다.

현재 강의의 종료 시점이 비교할 값의 시작 시점보다 작거나 같으면 그 강의실에 들어갈 수 있다. 아니면 새로 강의실을 만들어 큐에 추가한다.

중요한 건! 이렇게 했을 때 현재의 시작 시점과 종료 시점이 남은 것들 중에서 가장 최적을 뽑아낼 수 있어야 한다.
그래서 사전에 정렬을 진행해야 한다.

정렬 기준

현재 강의가 남은 강의 중에서 종료 시점이 가장 늦고, 시작 시점도 늦어야 이 값이 현재에서 최적의 비교값이 될 수 있다.

2. 정렬: 강의를 종료 시각이 큰 것부터, 같다면 시작이 큰 것부터 오게 정렬한다.

입력값이 (1,3), (2,4), (3,5) 라고 하면
(3,5), (2,4), (1,3) 으로 정렬이 완료된다.

이렇게 하면 종료시점이 늦은 애들부터 차곡차곡 쌓여서 최소의 강의실을 뽑아낼 수 있다.

코드

package solution;

import java.util.*;
import java.io.*;

public class BOJ11000_강의실배정 {
    static class Lecture implements Comparable<Lecture> {
        int s;
        int e;

        Lecture(int s, int e) {
            this.s = s;
            this.e = e;
        }

        @Override
        public int compareTo(Lecture o) {
            if(this.e == o.e) return o.s - this.s;
            return o.e - this.e;
        }
    }
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st;
        int N = Integer.parseInt(br.readLine());
        Lecture[] lectures = new Lecture[N];
        for (int i = 0; i < N; i++) {
            st = new StringTokenizer(br.readLine());
            lectures[i] = new Lecture(Integer.parseInt(st.nextToken()), Integer.parseInt(st.nextToken()));
        }
        Arrays.sort(lectures);

        PriorityQueue<Lecture> pq = new PriorityQueue<>((o1, o2) -> o2.s - o1.s);
        pq.add(lectures[0]);
        for (int i = 1; i < N; i++) {
            Lecture now = lectures[i];
            if(now.e <= pq.peek().s) {
                Lecture l = pq.poll();
                l.s = now.s;
                pq.add(l);
                continue;
            }
            pq.add(now);
        }
        System.out.println(pq.size());
    }
}