[Algorithm] 스위핑(Sweeping) (BOJ.1689 겹치는 선분 (java))

민지·2024년 7월 30일

Algorithm

목록 보기

7/8

스위핑

한 쪽을 기준으로 한 번 만에 전체 공간을 sweep, 쓸어오는 알고리즘.

기하학적 문제를 해결하는 데 사용되는 알고리즘적 접근 방식.
이 기법은 주어진 문제의 해를 찾기 위해 공간을 선형적으로 스윕(sweep)하면서 데이터를 처리한다.

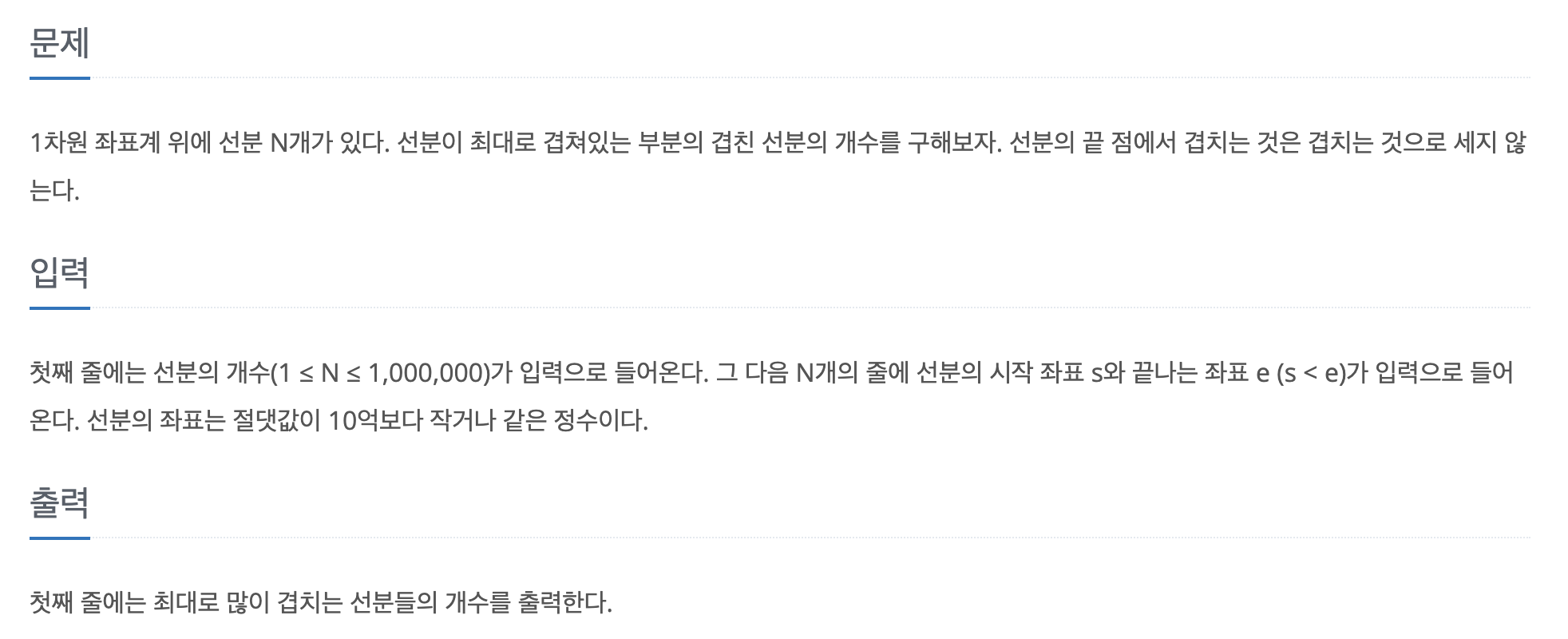
문제

겹치는 선분

접근 방법

처음 접근 흐름

정렬 + 그리디
선분의 시작 위치 + 종료 위치가 나오므로 정렬을 해서 값을 맞춰놓고 시작해야겠다고 생각.
시작 위치 작은 순 + 끝 위치 큰 순으로 하면 시작 위치 기준에서 가장 넓은 범위부터 좁혀지면서 값을 구해내려고 했다.
그리고 겹치는 구간의 가장 좁은 값을 저장해두고, 그 때의 cnt를 저장해두면,
그 다음 값이 갱신한다면, 그 뒤의 값은 더이상 앞의 선분을 찾지 않으니 그 때의 값이 최적의 해라고 생각했다.

근데 하나의 큰 선분(0,5)이 있을 때 (1,2)가 들어오면, 그 다음 (2,5)가 들어왔을 때 (0,5)를 어떻게 기억하고 있어야 될지 감이 안옴.

결국 알고리즘 분류를 보고 스위핑(sweeping) 이라는 처음보는 분류가 있었다.

다시 접근 방법

(결국 다른 사람의 풀이를 보았다.)

시작점과 끝점을 나눠서 각각 받아 우선순위큐에 저장.
수가 작은 순으로 정렬하고, 만약 같다면 끝점이 먼저 오게 한다.
시작점보다 끝점이 먼저 와야 하는 이유는 선분을 먼저 끝내고 cnt를 감소시켜야 하기 때문.
배열을 순회하면서, 시작점인 경우 겹친 선분을 +1 해준 후 max값을 갱신한다.
끝점인 경우 선분이 끝났으니 -1
최종 값 출력.

코드

package solution;

import java.util.*;
import java.io.*;

public class BOJ1689_겹치는선분 {

    static class Line implements Comparable<Line> {
        int node;
        int type;    // 시작(0), 끝(1)

        Line(int node, int type) {
            this.node = node;
            this.type = type;
        }

        @Override
        public int compareTo(Line o) {
            if (this.node == o.node) return o.type - this.type;
            return this.node - o.node;
        }
    }

    static final int START_TYPE = 0;

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st;
        int N = Integer.parseInt(br.readLine());
        PriorityQueue<Line> lines = new PriorityQueue<>();
        for (int i = 0; i < 2 * N; i+=2) {
            st = new StringTokenizer(br.readLine());
            lines.add(new Line(Integer.parseInt(st.nextToken()), 0));
            lines.add(new Line(Integer.parseInt(st.nextToken()), 1));
        }

        int ans = 1;
        int nowCnt = 0;
        while(!lines.isEmpty()) {
            Line line = lines.poll();
            if(line.type == START_TYPE) {
                nowCnt++;
                ans = Math.max(ans, nowCnt);
            } else {
                nowCnt--;
            }
        }
        System.out.println(ans);
    }
}