들어가며

기업별 빈출 알고리즘 문제집에 있는 문제들을 풀어나가고 있다.
코테를 꽤나 본 입장에서 정말 자주 만났던 문제라 한 번씩 정리하려고 해당 포스팅을 작성한다.

https://wikidocs.net/218199

문제

요격시스템

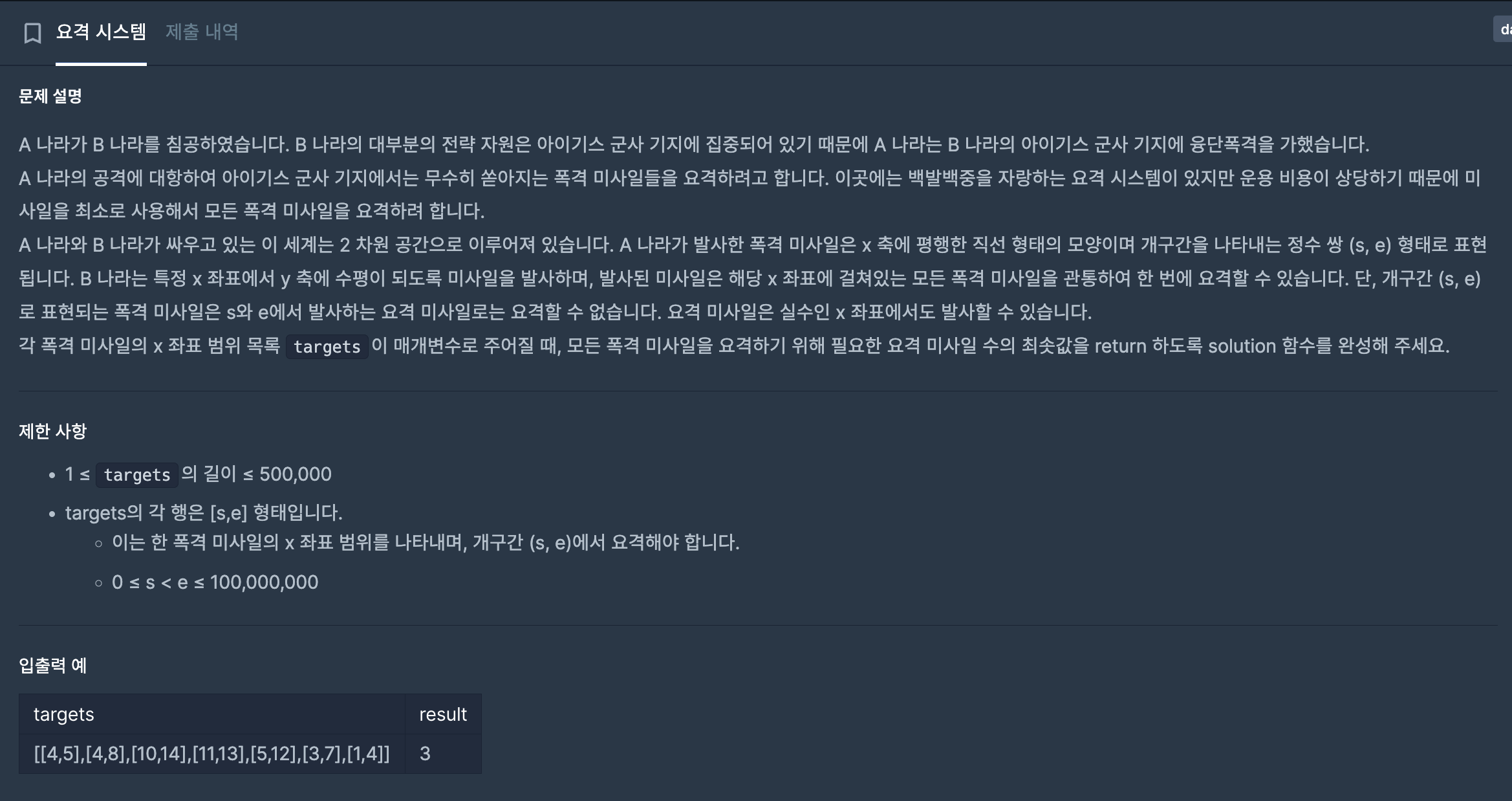
• 난이도: Level 2
• 선분들이 가장 많이 겹치는 구간들을 골라 최소한으로 횟수로 전체 선분을 선택하면 되는 문제
• 선분에서 시작점과 끝점을 가지고 최대/최소를 구하는 문제

접근 방법: 그리디

• 선분에서 시작점과 끝점을 가지고 최대/최소를 구하는 문제 ➡️ 정렬 + 그리디 일 확률이 크다.
• 기본적으로 인풋값이 10^8 이기 때문에 체크 배열을 만드는 건 불가능.
• 정렬 기준은 시작점과 끝점 2개뿐이다.

• 중간에 헤맨 부분이 최근에 스위핑 문제를 풀어서 시작점과 끝점을 나눠서 리스트를 만들고, 스택으로 괄호 개수 계산하는 방식으로 접근하려 했다.
  • (1,s), (3,s), (4,e), ... 이런식으로
• 이 문제는 본인의 시작과 끝이 명확히 짝이 지어져 있었기 때문에 같이 들고 다니는 게 맞다고 생각함.

시작점을 기준으로 두고, 현재 선분이 이전 선분과 비교해서 겹치는 지, 아닌지만 판별하면 된다.
끝점은 관계없다.
정렬되지 않아도 그 이후에 Math.min 으로 비교해주기 때문.

통과 코드

import java.util.*;
import java.io.*;

class Solution {
    
    static class Line implements Comparable<Line> {
        int s;
        int e;
        
        Line(int s, int e) { 
            this.s = s;
            this.e = e;
        }
        
        @Override
        public int compareTo(Line o) {
            return this.s - o.s;
        }
        
    }
    
    public int solution(int[][] targets) {
        int answer = 0;
        List<Line> lines = new ArrayList<>();
        for(int i = 0; i < targets.length; i++) {
            lines.add(new Line(targets[i][0], targets[i][1]));
        }
        Collections.sort(lines);
        
        int nowS = 0;
        int nowE = 0;
        for(Line l : lines) {
            // 안겹칠때
            if(nowE <= l.s) {
                answer++;
                nowS = l.s;
                nowE = l.e;
            } else {
                nowS = Math.max(nowS, l.s);
                nowE = Math.min(nowE, l.e);
            }
        }
        
        return answer;
    }
}

결과

• 풀이 시간: 28m
• 처음에 접근을 잘못해서 15분 정도 허비했다. 23m 쯤 지날때 정렬 기준을 시작값에만 맞추면 된다고 판단하고, 겹치는 구간과 겹치지 않는 구간으로 나누어 개수를 판별했다.

마치며

정렬 기준만 금방 확인했다면 5분안에 풀었을 문제이고, 실전에서 만나면 그렇게 해야한다..