Kruskal's Algorithm

오늘은 Kruskal's Algorithm에 대해 배우고, 해당 슈더코드를 C++로 구현까지 해보았다.
Kruskal's Algorithm은 MST를 만들기 위한 알고리즘이다. 모든 노드를 최소한의 비용으로 '연결'시켜야 하는 것이기 때문에 edge를 오름차순으로 정렬하고, 정렬된 edge를 순서대로 포함시키는 방법을 이용한다.

1. node들을 disjoint sets으로 만든다.
2. edge들을 오름차순으로 정렬한다.
3. edge들 중 weight가 가장 적은 것을 선택한다.
4. 해당 edge가 연결하는 node들을 한 집합으로 병합한다.
5. 해당 edge를 집합에 넣는다.
6. 과정 3~5를 edge의 수가 (node의 수-1)이 될 때까지 반복한다.

이 6개의 과정을 슈더코드로 작성해보면 이러하다.

 F = ∅;    //오름차순의 edge들이 차례대로 정렬될 집합 F 초기화
 
 create disjoint subsets of V, one for each vertex and containing only that vertex;
 
 sort the edges in E in nondecreasing order;
 
 While(the instance is not solved){
 	select next edge;
    
    if(the edge connects 2 vertices in disjiont subsets){
    	merge the subsets;
        add the edge to F;
    }
    if(all the subsets are merged)
    	the instance is solved;
 }

이러한 슈더코드를 기반으로 하여 C++로 구현해보았다.

#include <iostream>
#include <vector>
#include<algorithm>

using namespace std;

const int n = 5;
typedef int index;
typedef index set_pointer;

struct nodetype {
	index parent;
	int depth;
};
typedef nodetype universe[5];
universe U;
void makeset(index i) {
	U[i].parent = i;
	U[i].depth = 0;
}
set_pointer find(index i) {
	index j;
	j = i;
	while (U[j].parent != j)
		j = U[j].parent;
	return j;
}
void merge(set_pointer p, set_pointer q) {
	if (U[p].depth == U[q].depth) {
		U[p].depth = +1;
		U[q].parent = p;
	}
	else if (U[p].depth < U[q].depth) U[p].parent = q;
	else U[q].parent = p;
}
bool equal(set_pointer p, set_pointer q) {
	if (p == q) return true;
	else return false;
}
void initial(int n) {
	index i;
	for (i = 1; i <= n; i++)
		makeset(i);
}

typedef int set_of_edges[n-1][3];
typedef int edge;
set_of_edges F;
void kruskal(int n, int m, int E[][3], set_of_edges& F) {
	index i, j, l;
	set_pointer p, q;
	edge e;

	sort(E, E + m);
	
	
	for (i = 0; i < n-1; i++)
		F[i][0] = 0;
	initial(n);

	l = 0;
	while (F[n - 2][0] != 0) {
		e = E[l][0];
		i = E[l][1];
		j = E[l][2];

		p = find(i);
		q = find(j);
		if (!equal(p, q)) {
			merge(p, q);
			F[l][0] = e;
			l++;
		}
	}
}
int main() {
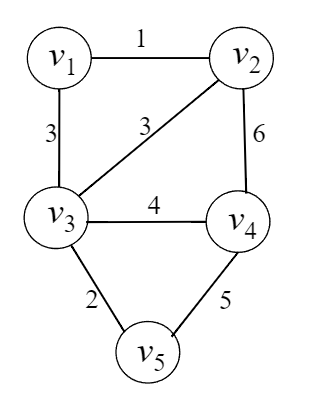
	int edges[7][3] = {{1,1,2},{3,1,3},{3,2,3},{6,2,4},{4,3,4},{2,3,5},{5,4,5}};
	kruskal(5, 7, edges, F);
	for (int i = 0; i < n - 1; i++)
		cout << F[i][0];
	
}

edge가 7개이고 node가 5개인 그래프의 MST를 찾는 kruskal's algorithm이다.

해당 그래프로 코드를 테스트 해보면 결과는 이러하다.

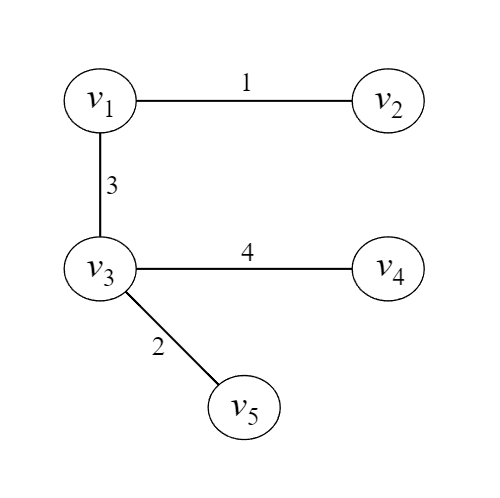
그리고 이 결과를 그래프로 나타내보면

이런 MST가 도출됨을 알 수 있다.