Dijkstra's Algorithm

오늘은 Dijkstra's Algorithm에 대해 배우고, C++로 구현해 보았다.
Dijkstra 알고리즘은 가중치가 있는 방향성 그래프에서 한 특정 정점에서 다른 모든 정점으로 가는 최단 경로를 구하는 문제이다.
Dijkstra 알고리즘은 최단 경로를 구할 때 그 전까지 구했던 최단 거리 정보를 가져와 사용하기 때문에 Dinamic Programming 문제라고 할 수 있다. (작은 문제가 큰 문제의 부분 문제가 됨)

1. 선택된 edge를 저장할 집합과 선택된 vertex를 저장할 집합을 생성한다.
2. 시작 지점을 정한다.
3. 아직 선택되지 않은 vertex 중 선택된 vertex 집합에 있는 vertex만 이용하여 시작점에서부터 최단 거리인 vertex를 선택한다.
4. 해당 vertex와 그를 가리키는 edge를 선택하여 집합에 포함시킨다.
5. 3, 4를 반복하다가 선택된 vertex의 집합이 전체 vertex 집합과 같아지면 끝난다.

이것을 슈더코드로 나타내면 이러하다.

F = 0;        //선택된 엣지를 저장할 집합
Y = {v1};     //선택된 vertex를 저장할 집합, v1은 시작 정점으로, 미리 넣어둔다.
While (the instance is not solved){
	select a vergtex v from(V - Y), that has a shortest path from v1,
    using only vertices in Y as intermediate; //집합 V는 전체 vertex 집합을 의미한다.
    
    add the new vertex v to Y;
    add the edge that touches v to F;
    
    if (Y==V)
    	the istance is solved;   
}

이 슈더코드를 C++로 구현해 보았다.

#include <iostream>
#include <vector>
using namespace std;

const int v = 5;
vector<vector<int>> W(v,vector<int>(v-1,10000));
vector<int> F;

void dijstra(int n, vector<vector<int>> W , vector<int>& F) {
	int i, vnear, e;

	vector<int> touch;
	
	vector<int> length;
	
	for (i = 0; i < n-1; i++) {
		touch.push_back(1);
		length.push_back(W[0][i]);
	}
	int vvnear = 0;
	int count = 0;
	while (count < n-1) {
		int min = 10000;
		for (i = 0; i < n-1; i++) {
			if (0 <= length[i] && length[i] <= min) {
				min = length[i];
				vnear = i;
			}
		}
		e = W[touch[vnear]-1][vnear];
		F.push_back(e);
		for (i = 0; i < n-1; i++) {
			if (length[vnear] + W[vnear+1][i] < length[i]) {
				length[i] = length[vnear] + W[vnear+1][i];
				touch[i] = vnear+2;
			}
		}
		int a = length[0], b = length[1], c = length[2], d = length[3];
		vvnear = vnear+1;
		length[vnear] = -1;
		count++;
	}

}
void putW(int source, int dest,int weight) {
	
	W[source - 1][dest - 2] = weight;
}
int main() {
	putW(1, 2, 7);
	putW(1, 3, 4);
	putW(1, 4, 6);
	putW(1, 5, 1);
	putW(3, 2, 2);
	putW(3, 4, 5);
	putW(4, 2, 3);
	putW(5, 4, 1);

	dijstra(v, W, F);

	for (int i = 0; i < v-1; i++) {
		cout << F[i] << " ";
	}
}

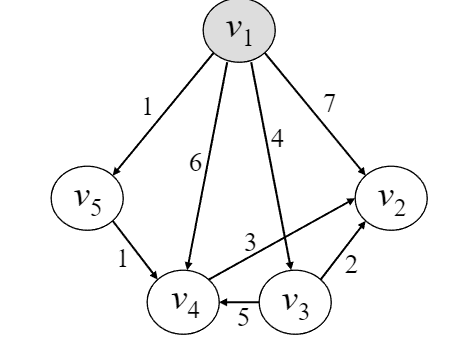
테스트용 그래프는 이러하다.

출력 결과:

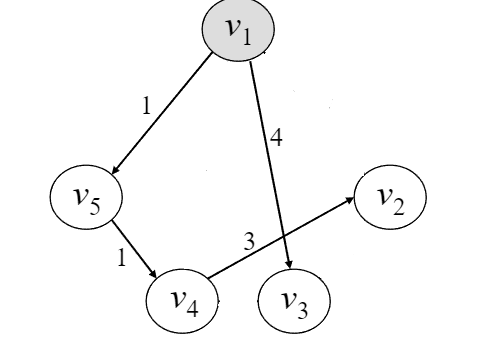
출력 결과를 통해 얻을 수 있는 그래프의 형태이다.