Flow Networks

Network는 보통 directed graph G = (V, E)로 표현이 됩니다.
이전 graph 알고리즘을 다룰 때에도 언급을 했지만, |V| = n, |E| = m이 되겠습니다.

capacity

각각의 edge e는 capacity c(e) ≥ 0을 가지고 있고, 이 c(e)라는 것은 해당 edge의 한계 traffic등으로 생각할 수 있습니다.

source / sink

network에는 최소 한 개 이상의 traffic/data source와 sink를 가집니다. (출발, 도착)
traffic은 항상 source에서 sink로 흐릅니다. (flow)
그리고, traffic은 network의 각 vertex에서 교차됩니다.

Flow

Source에서 sink로 흐르는 traffic/data 등을 나타내는 abstract term입니다.

Traffic은 flow의 한 종류입니다.
근데 이런 것들은 단위를 정의하기가 많이 힘들기 때문에...
앞으로는 traffic이라는 용어 대신 flow라는 용어를 사용하겠습니다.

Network

어떤 지점과의 연결을 나타내는 그래프를 network라고 부를 것입니다.
그냥 이름이 network일 뿐이고... 별 다른 의미를 담고 있지는 않은 것 같네요.

그리고, 이 그래프는 directed graph라고 가정할 것입니다.
보통 흐르는건 어느 한 쪽으로 흐르는게 일반적이니까, 일반적으로 더 많은 case를 cover할 수 있는게 directed graph이기 때문입니다.

Assumption

Single Source, Single Sink Flows

Single source vertex s, Single sink vertex t가 존재합니다. 이 외의 다른 모든 vertex들은 internal vertex라고 불립니다.
s에서 t로 전달이 될 것이고, 각각의 edge e는 capacity c(e)를 가지고 있습니다.
source s는 incident한 incoming edge가 없고(in-degree = 0), sink t는 incident한 outgoing edge가 없습니다. (out-degree = 0)

Capacity: Positive integer

그리고 여기서 capacity는 positive integer라고 가정할 것입니다. 이 조건이 상당히 중요하기 때문에 한 번 짚고 넘어가는 것입니다.

No Isolated Vertex (Connected Graph)

또한 모든 vertex는 적어도 한 개의 incident한 edge를 가지고 있다고 가정하겠습니다.

Definition of the Flow

flow를 formal하게 정의할 것입니다. 정의하는 방법은 edge-based, path-based로 두 가지가 있고, 이 둘은 equivalent합니다.
equivalent한데 왜 따로 다루냐? 하면 두 개가 다른 특징을 가지고 있기 때문에, 필요에 따라서 사용하기 위함입니다.

Edge-Based

path-based 보다 더 일반적입니다.
말 그대로 edge에 대해 정의가 된 것입니다.
flow를 함수로 정의하는데 이 함수는 function f: E → R$^{≥0}$ 입니다.
근데 이 함수가 그냥 마음대로 non negative real number면 된다? 는 아니고 Constraint가 존재합니다. 이 두 가지 제약조건을 만족해야 valid한 flow function이라고 할 것입니다.

Capacity Constraint

각각의 edge e에 대해서 f(e) ≤ c(e)

진짜 쉽게 생각할 수 있습니다.
만약 어떤 배관에 물을 한 번에 최대 10 L 흘려보낼 수 있다고 했을 때, 이 배관에 11 L의 물을 한 번에 흘려 보낼 수는 없습니다.

Conservation Constraint

각 vertex v ≠ s, t(s는 source, t는 sink)에 대해 $Σ_{e\ into\ v} f(e) = Σ_{e\ out\ of\ v} f(e)$
$Σ_{e\ into\ v} f(e)$와 $Σ_{e\ out\ of\ v} f(e)$를 각각 $f^{in}(v)$ 및 $f^{out}(v)$로 표기하며, 마찬가지로 vertex set A에 대해 $f^{in}(A)$ 및 $f^{out}(A)$도 동일하게 정의한다.

Network G에서 flow의 value v(f)는 $f^{out}(s)$로 정의한다.

이게 대체 무슨 말이냐... 보존을 잘 한다고 받아들이면 됩니다.
물이 5 L와 5 L가 들어왔는데, 나가는 게 10 L, 20 L가 되면 안 되겠죠? 그리고, 5 L를 받았는데, 그 중에서 3 L를 아껴놨다가 다음에 내보낸다든지 그런 건 안된다고 이야기하는 것입니다. 이게 바로 conservation constraint라고 생각하면 될 것 같습니다.

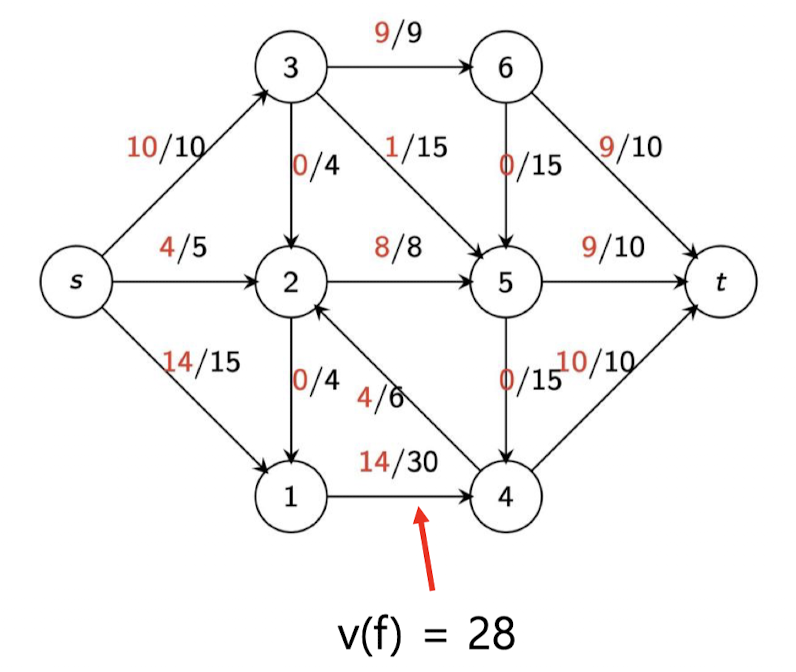
Path-based

마찬가지로 flow function을 정의할 것입니다. 이름이 path-based니까 edge대신 path에 대해서 정의를 해야겠죠? 이는 function f: P → R$^{≥0}$ 로 정의됩니다.
flow는 path를 따라 s에서 t로 간다는 점을 생각해야 합니다.
P를 s에서 t로의 모든 path의 set이라고 해봅시다! 이 경우에는 최악의 경우(complete graph의 경우?) |P| = n!이 될 수 있습니다.
s-t path가 domain이므로 domain size가 m인 edge-based보다 훨씬 domain size가 클 것입니다. 그래서 이걸 그냥 써버리면 공간 낭비가 심할 수 있는데...
일단 정의부터 해보겠습니다.
여기서도 똑같이 제약 조건이 존재합니다.

Capacity Constraint

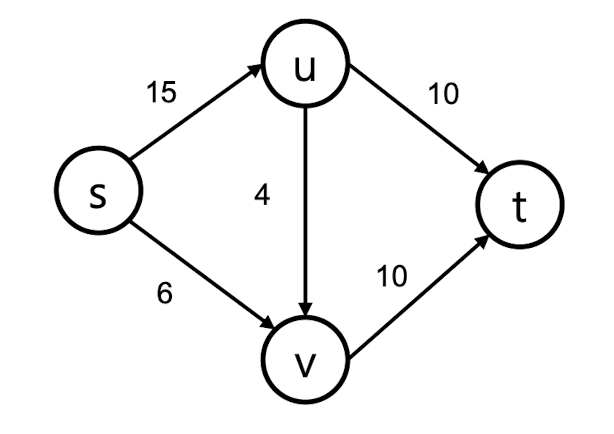
이 그림에서 s-t path는 3개입니다. (s->u->t / s->u->v->t / s->v->t) 이들 각각을 $p_1, p_2, p_3$ 라고 해보겠습니다. edge-based에서는 각각의 edge에 대한 함수를 만들었지만, path-based에는 path에 대한 함수를 만든다고 했습니다. (여기서 주의할 점은 path를 다룬다고 해서 capacity를 새로 정의하는 것이 아닙니다. capacity는 여전히 edge에만 존재하고, 이건 고정이 되어 있습니다.)

근데, 우리는 그래프를 지금 다룰 그래프에 존재하는 path는 모두 s-t path라고 가정했었습니다. 그럼, 그래프에 있는 어떤 edge를 잡아도 s-t path에 있는 edge일 것입니다.

이 내용을 토대로 $P_e$를 e를 포함하는 모든 P상의 path라고 정의하겠습니다. 각 edge e에 대해서 e의 total flow는 최대 c(e)이고, $Σ_{p ∈ P_e} f(p) ≤ c(e)$가 성립합니다.

Conservation Constraint

edge-based에서 봤듯이 들어오면 반드시 들어온 양만큼 나와야 합니다. path-based로 생각하면, 어차피 vertex에 이어진 path를 따라서 같은 flow value가 정의되기 때문에 이는 정의할 필요가 없습니다. 자동적으로 성립되기 때문이죠.

Network G의 flow value를 정의할 것인데, edge-based에서는 source에서 나가는 총 합으로 정의를 했었습니다. 근데 이번에는 Path가 source에서 sink로의 path이고, 각 path마다 non-negative flow value를 정의해주었기 때문에 단순히 모든 path에 대한 path-based flow 값을 정해준 $Σ_{p ∈ P} f(p)$로 정의합니다.

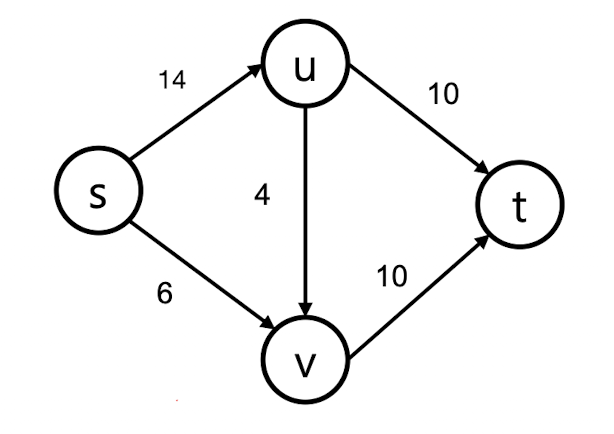
위 그림을 예시로 들어보겠습니다.
P = {$p_1, p_2, p_3$}
$p_1$ = s → u → t
$p_2$ = s → u → v → t
$p_3$ = s → v → t
라고 했을 때,
f($p_1$) = 10, f($p_2$) = 4, f($p_3$) = 6이 되고
Network G의 flow value는 20이 되겠습니다.

Edge-based flow vs. Path-based flow

혹시 두 개가 다를 경우가 있나? 를 생각해볼 수 있습니다. 앞서 언급했듯이 두 정의는 equivalent하기 때문에 그럴 경우는 없지만! 왜 equivalent한 지 알아보기는 해야겠습니다.

Lemma: Path-based flow f: P → R$^{≥0}$가 주어졌을 때, 같은 value를 가지는 edge-based flow f': E → R$^{≥0}$이 존재한다.

Proof
Edge e에 대해서 $f'(e) = Σ_{p:e∈P} f(p)$두 flow의 value가 동일하지 않다고 가정해보겠습니다. 이 경우 path-based definition과 해당 그래프 구조의 가정 자체에 모순이 생깁니다.
따라서 $f'(e) = Σ_{p:e∈P} f(p)$이며, path-based definition에서 제시된 두 가지 constraints에 따라 path-based deifinition으로 정의된 edge-based flow value 또한 두 가지 제약 조건을 만족함을 알 수 있습니다.

Lemma (flow decomposition): f'과 f를 각각 위 Lemma에서 정의한 edge-based flow와 path-based flow라고 하자. 이 때 f'이 주어진 경우, 같은 value를 가지는 flow f를 O(m(n+m)) time에 구할 수 있다.

Proof
아래와 같은 Procedure를 통해서 f를 정의할 수 있습니다.
1. f'(e) = 0인 모든 edge e를 제거합니다.
2. s에서 t로의 path p를 하나 찾습니다.
3. $f(p) = min_{e∈p}f'(e)$로 정의합니다.
4. 모든 e∈p에 대해 f'(e)를 f(p)만큼 감소시킵니다.
5. 1-4를 s에서 t로의 path가 없을 때까지 반복합니다.

여기서, 1~4 과정에서 O(m+n) time이 소요되고, 최대 m번의 iteration을 하므로(탐색할 것이 m개에서 m-1개, m-2개, ... 가 되기 때문에) O(m(n+m)), time이 걸립니다.

f랑 f'의 값이 같다는 것은 과정을 따라가보면 쉽게 알 수 있습니다!!

Edge-based flows

• Compact 한 representation! (domain size가 edge의 개수인 m이 됩니다)
• Flow conservation을 각 internal vertex마다 확인해주어야 합니다.

Path-based flows

• Compact 하지 않습니다. (앞서 언급했듯이 domain size가 최대 n!개 입니다)
• Flow conservation을 확인할 필요가 없습니다.

domain size가 edge-based flow가 훨씬 작으니 edge-based flow만 사용하면 되지 않나??? 할 수도 있겠지만, 몇몇 application의 경우에는 path-based definition이 더 자연스러울 수가 있습니다.
우리는 둘이 equivalent 함을 증명까지 했으니, 상황에 따라서 유리하거나 더 편한 정의를 사용하면 됩니다!!