그래프에 관련된 알고리즘을 알아볼 것입니다.
그 전에, 자료구조에서 배웠던 알고리즘 관련 용어들을 복습해보겠습니다.

Graph Terminology Review

Graph

Graph G는 vertex들의 집합 V(G)와 두 vertex로 구성된 edge들의 집합 E(G)로 구성되어 있는 구조입니다. G = (V(G), (E(G))로 표기하고, G가 명확한 경우에는 보통 G = (V, E)로 표기합니다.

Simple Graph

Self-loop나 multiple edge를 가지지 않는 graph를 의미합니다. self-loop와 multiple edge의 의미는 아래 그림에서 직관적으로 알 수 있습니다.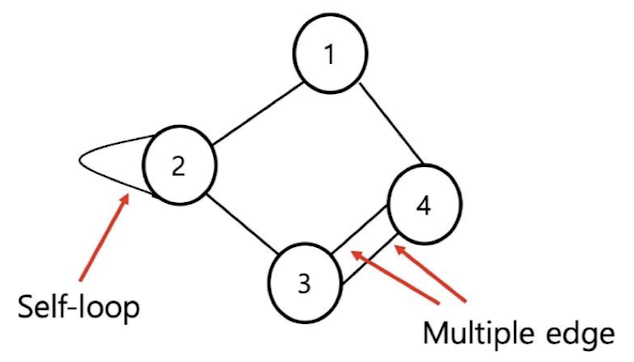
위처럼 self-loop나 multiple edge가 존재하는 그래프는 multigraph라고 합니다. 하지만, 이 수업에서는 웬만한 모든 graph는 simple graph라고 가정할 것입니다.

Directed graph

E의 각 원소들은 ordered pair임을 의미합니다. 이게 무슨 의미냐면... 그래프의 edge들이 방향성을 가지고 있음을 의미합니다.

Undirected graph

E의 각 원소들은 unordered pair임을 의미합니다. 이는 directed graph와 반대로 edge들이 방향성을 가지고 있지 않음을 의미하겠죠?

아래의 그림을 참고하면 directed graph와 undirected graph의 차이를 알 수 있을 것입니다.

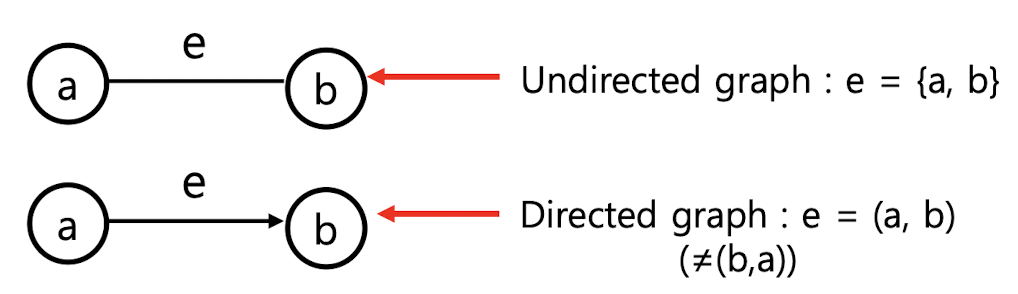
adjacent

vertex v와 u에 대해 (v, u)∈E 일 때, v는 u와 adjacent하다 라고 합니다.
위 그림에서 알 수 있다시피, undirected graph에서는 a가 b와 adjacent하면서 b가 a와 adjacen하다고도 말할 수 있습니다.

Degree of v

G에서 하나의 vertex v에 연결된 edge 수를 의미합니다.

neighbor

Edge(u, v)가 있는 경우, v는 u의 neighbor라고 합니다.

in-degree, out-degree

directed graph에 존재하는 개념입니다. in-degree는 하나의 vertex로 들어오는 edge 수를, out-degree는 반대로 하나의 vertex에서 나가는 edge 수를 의미합니다.

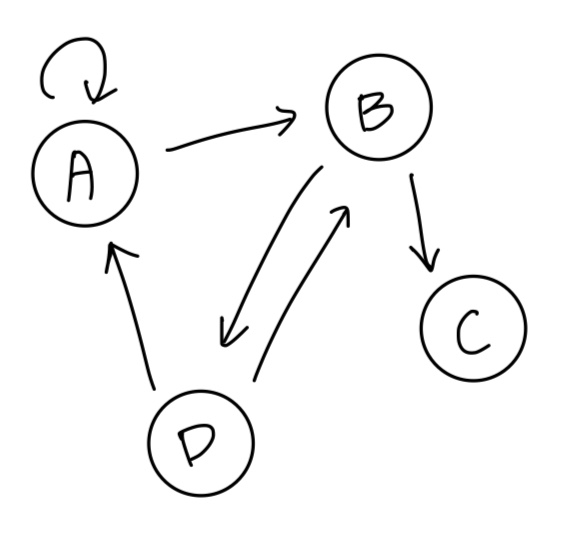
이런 그래프가 있다고 해봅시다.
여기서 A의 in-degree는 A에서 A로 들어오는 edge, D에서 A로 들어오는 edge로 총 2가 될 것입니다. 반대로, out-degree는 A에서 A로 나가는 edge, A에서 B로 나가는 edge로 총 2가 될 것입니다.
한 가지 경우를 더 살펴보자면, D의 in-degree는 B에서 D로 들어오는 edge로 총 1이 될 것이고, out-degree는 D에서 A로 나가는 edge, D에서 B로 나가는 edge로 총 2가 될 것입니다.

위 예시에서 한 가지 더 알 수 있는 것은 self-loop는 in-degree, out-degree 모두의 counting에 포함이 된다는 것입니다!

Subgraph

graph G = (V(G), E(G))에서 graph G의 subgraph G' = (V(G'), E(G'))는 다음과 같은 조건을 만족합니다.

i) V(G') ⊆ V(G)
ii) E(G') ⊆ E(G)
이 때, E(G')의 모든 edge는 V(G')의 vertex만을 사용해야 합니다.
반대로 V(G')은 E(G')에 없는 vertex를 추가적으로 가질 수 있습니다!

Walk

walk는 $v_1, e_1, v_2, e_2, ... , e_k, v_k$로 이어지는, vertex $v_1, v_2...$와 edge $e_1, e_2...$가 서로 교차되며 나타나는 (alternating) sequence를 의미합니다. 이 때, edge $e_i = (v_i , v_{i+1})$입니다.
simple graph에서는 보통 edge의 표기를 생략합니다

Trail

같은 edge가 두 번 이상 반복되지 않는 walk

Path

같은 vertex가 두 번 이상 반복되지 않는 walk

Circuit

시작 vertex와 마지막 vertex가 같은 trail을 의미합니다.

Cycle

시작 vertex와 마지막 vertex를 제외하고 같은 vertex가 두 번 이상 반복되지 않는 circuit을 cycle이라고 합니다.

위 5개의 개념은 그냥 글로 보면 이해가 잘 되지 않으니 그림과 함께 보도록 하겠습니다.

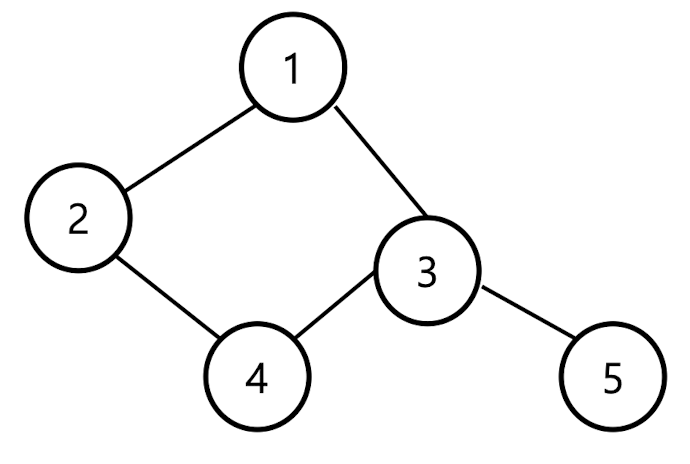
• Walk: 1 -> 2 -> 4 -> 3 -> 5 -> 3
• Trail (1-5): 1 -> 2 -> 4 -> 3 -> 5
• Path (1-5): 위와 동일 (정의를 생각하면 왜 같은 지 알 수 있습니다!)
• Circuit: 1 -> 2 -> 4 -> 3 -> 1 (또는, 1 -> 2 -> 4 -> 3-> 5 -> 3 -> 1)
• Cycle: 1 -> 2 -> 4 -> 3 -> 1

그래프 문제 관련된 정의에서는 기호를 많이 쓰기 때문에, string algorithm 처럼 그려서 이해해보면 조금 이해가 수월할 것입니다.

Connectivity

Undirected graph G = (V, E)에서 G가 connected이다 라는 말은,
임의의 서로 다른 두 vertex v, w ∈ V에 대하여 v에서 w로의 path가 존재함을 의미합니다.
이 경우에 G를 connected graph라고 합니다.
만약, connected하지 않다면, disconnected하다고 하겠죠?

directed graph에 대해서는 나중에 따로 정의를 할 것입니다.
따로 정의하는 이유 또한, undirected graph와 directed graph의 정의를 생각해보면 될 것 같네요.

Adjacency matrix / list

vertex가 n개인 Graph G를 저장하는 방법입니다.

Adjacency martix

G를 n*n matrix(array)를 이용해서 저장합니다.

Adjacency list

G를 n개의 서로 다른 list들을 이용해서 저장합니다.

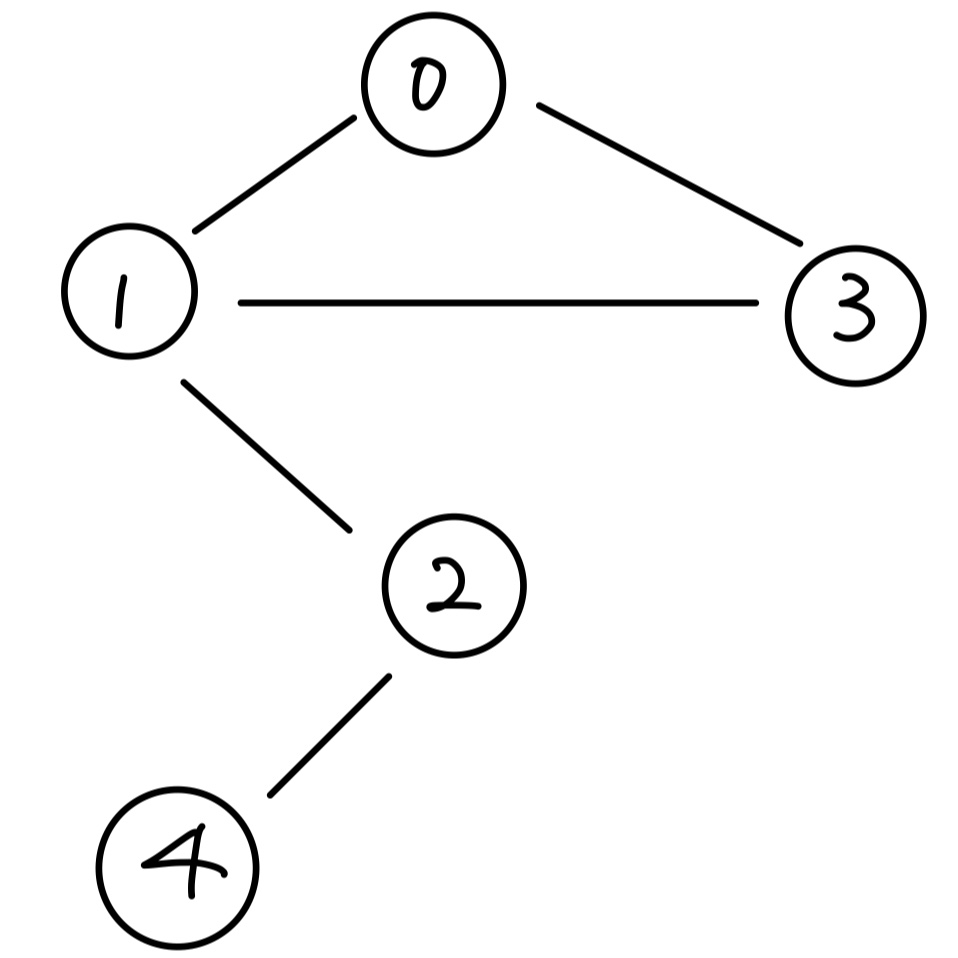
위 그래프에 대한 adjacency martic와 adjacency list는 각각 다음과 같습니다.

(u, v) ∈ E 인 경우 1로 표기하고, 그렇지 않은 경우 0으로 표기합니다.
undirected graph의 경우, (n, m) = 1인 경우 (m, n) = 1이 성립되기 때문에 symmetric matrix의 형태를 가집니다!

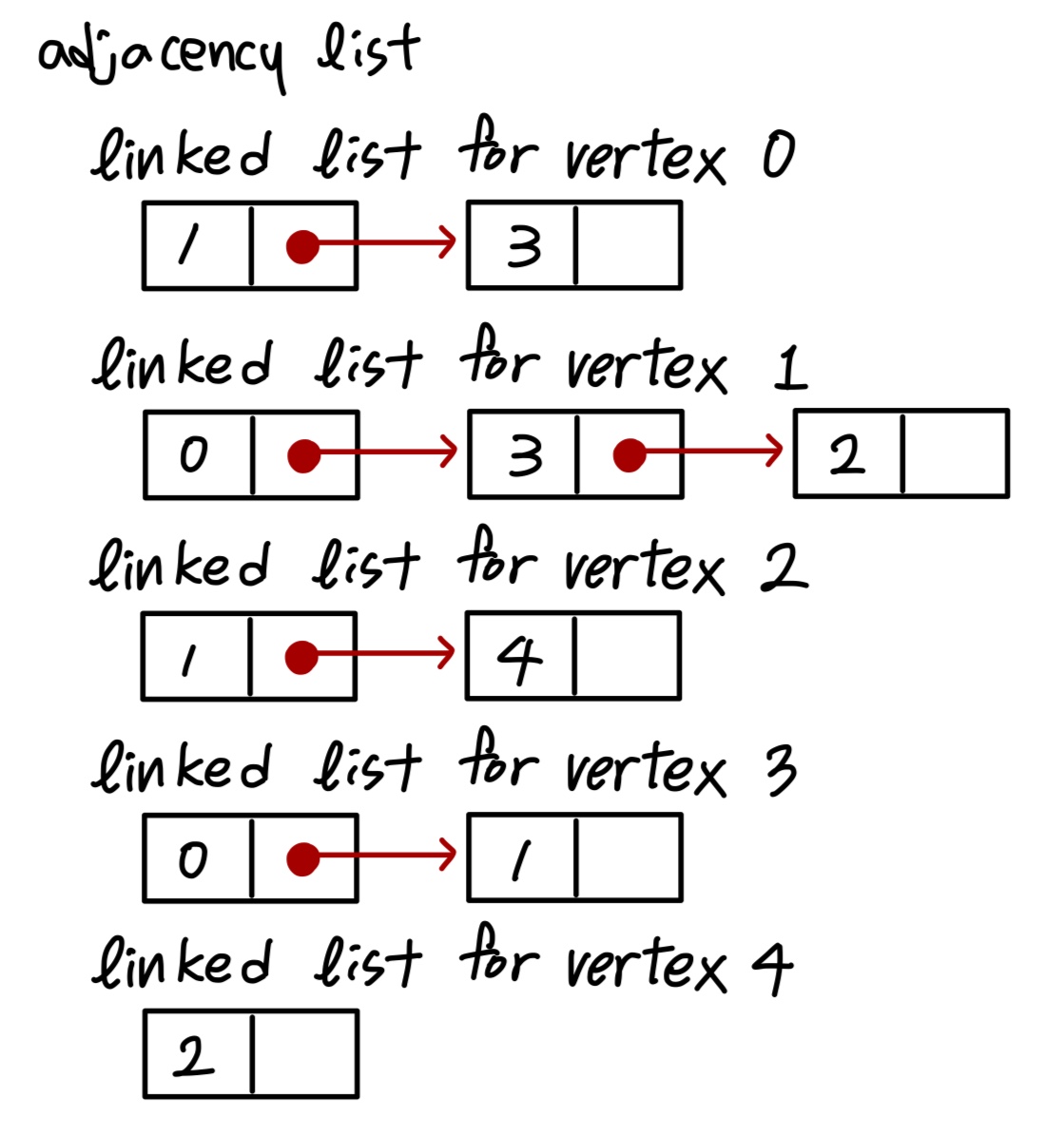
adjacency한 vertex들을 연결합니다.
adjacency list의 총 node 개수는! $Σ_{_{v ∈ V}}$deg($V$) = 2$|E|$ 가 됩니다. undirected graph의 특징을 상기시켜보면 바로 이해가 될 것입니다.
((n, m) ∈ E이면, (m, n) ∈ E 이므로!)

Adjacency matrix vs. Adjacency list

두 자료구조의 성능을 비교해보아야겠죠?
(앞으로 특별한 일이 없으면 |V| = n, |E| = m 이라고 합시다)
(+ 우리는 simple graph를 가정하므로, |E| ≤ $(^n_2)$ = n(n+1)/2가 됩니다.)

	Adjacency Matrix	Adjacency List
Space	$O(n^2)$	$O(n+m)$
Vertex u과 v가 adjacent 한 지 확인	$O(1)$	$O(deg(u))$
Vertex u의 모든 neighborhood 탐색	$O(n)$	$O(deg(u))$
deg(u) 답하기	$O(n)$	$O(deg(u))$
모든 edge scan	$O(n^2)$	$O(n+m)$

vertex u v의 adjacent 여부를 확인하는 경우를 제외하고는 Adjacency list가 더 우세한 성능을 가지고 있는 것을 알 수 있습니다.
앞으로 모든 graph관련 알고리즘은 graph가 adjacency list에 저장되어 있다고 가정할 것입니다!

Reachability

Undirected graph G의 두 vertex u, v에 대하여 u에서 v로의 path가 존재한다면, v는 u로부터 reachable하다고 합니다.

• 우리는 Graph G의 vertex v가 주어질 때, v에서 reachable한 모든 vertex를 어떻게 찾을 수 있을까요?

explore(G, v)

v ∈ V에서 reachable한 모든 vertex들을 찾는 procedure입니다.

Input: G = (V, E) is a graph;
Output: visited(u) is set to true for all nodes u reachable from v

visited(v) = true
previsit(v)
for each edge (v, u) ∈ E:
	if not visited(u): explore(u)
postvisit(v)

Vertex v를 탐색할 때마다 v와 adjacent한 vertex 중 아직 방문하지 않은 vertex를 recursively하게 방문합니다.

Theorem: explore(G, v)는 올바르게 동작한다.

proof)
"explore(G, v) procedure가 v에서 reachable한 어떤 vertex u를 방문하지 않는다" 라고 가정하고, 이 때 z가 'v에서 u 사이의 path에 있는 vertex들 중 마지막으로 방문한 vertex'라고 하자.

이제 vertex w가 v-u path에서 z 바로 다음에 나오는 vertex라고 가정하면, (z, w) ∈ E 임에도 불구하고 방문하지 않는다.
→ z와 adjacent한 모든 vertex를 방문한다는 사실에 모순이다!

"explore(G, v) procedure가 v에서 reachable하지 않은 어떤 vertex u를 방문한다" 라고 가정하고, 이 때 z가 'v에서 u 사이의 path에 있지 않은 vertex'라고 하자.

이제 vertex w가 v-u path에 존재하는 임의의 vertex라고 가정하자. 여기서, vertex z를 방문하려면, (w, z) ∈ E 이어야 하지만, z의 정의(v-u 사이 path에 있지 않은 vertex)에 의해 어떤 w에 대해서도 (w, z) ∈ E가 존재하지 않다. 따라서 vertex z를 방문할 수 없다.
→ v에서 reachable하지 않은 z를 방문한다는 가정에 모순이다!

따라서, explore(G, v)는 올바르게 동작함을 알 수 있습니다.

Procedure

procedure 시작 전 1로 초기화한 변수 counter를 하나 둔다고 합시다.

1. previsit(v)를 할 때마다 pre(v)
2. postvisit(v)를 할 때마다 post(v)

의 값을 현재 count의 값으로 설정하고, counter의 값을 1 증가시킵니다.

이와 같이 vertex v에 대해서 정의된 값 pre(v)와 post(v)를 각각 v의 preorder number와 postorder number라고 해봅시다.

앞선 explore 연산의 수행 과정을 ordered tree로 나타낼 수 있습니다.
이를 흔히 DFS tree라고 합니다.

1. DFS의 tree의 root는 explore를 시작하는 vertex입니다.
2. explore(G, v) 수행 도중 explore(G, u)를 호출할 경우, u는 v의 child node가 됩니다.
3. Graph G의 edge들 중 DFS tree에 있는 edge를 tree edge, DFS tree에 없는 edge를 back edge라고 하며, 전자는 보통 실선, 후자는 점선으로 나타냅니다.

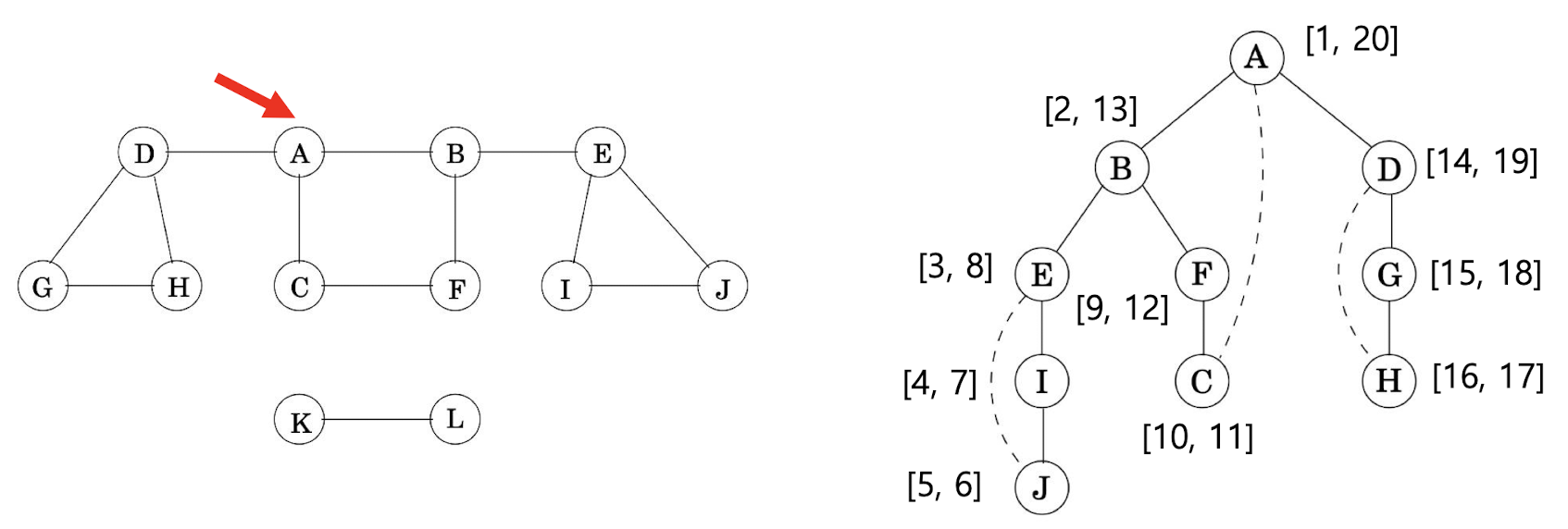
DFS

앞서 언급한 explore procedure를 이용해서, graph 상에 있는 모든 vertex를 한 번씩 방문하는 방법입니다.

for all v ∈ V:
	visited(v) = false
    
for all v ∈ V:
	if not visited(v): explore(v)

방문하지 않은 vertex 중 아무 vertex를 하나 골라 해당 vertex에서 explore procedure를 수행합니다. 이 작업을 모든 vertex를 방문할 때까지 반복합니다.

수행 시간은?

• 모든 vertex에 대해서 visited(v)를 초기화 → $O(n)$
• 모든 vertex에 대해서 explore를 하는 시간: explore 도중 같은 edge를 최대 두 번 access 한다. (adjacency list를 어떻게 만들었는지 생각해보면 됩니다!) → $O(m)$

⇒ $total\ O(n+m)$