Phase 3

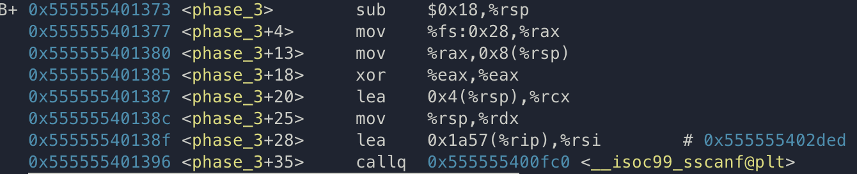
phase 3 입니다. 이 친구는 입력 값을 직관적으로 알 수는 없을 것 같네요.

scanf에서 rsi가 어떻게 생겼는지 확인해보겠습니다.

정수 두 개를 입력 받네요. 이를 토대로 입력 값을 수정하고 다시 진행해보겠습니다.

eax는 scanf의 반환 값이니 입력 값의 개수이지 않을까요?

<+40>에서 1과 비교하고 <+43>에선 1보다 작거나 같으면 <+74>로 분기합니다.

<+74>에는 뭐가 있나 봤더니

터지네요.

입력 형식을 "%d %d"로 확인해서 2개로 입력 받아야 한다는 것을 알았지만,

<+40> ~ <+43>에선 이 조건이 충족되지 않으면 폭탄을 터뜨립니다.

그러니, 이 뒤를 진행할 때에는 폭탄이 터지지 않게 입력 값을 바꾸고 진행해야 합니다.

이미 바꿔놨으니 바로 진행해보겠습니다.

<+45>에서 첫 번째 입력 값과 7을 비교합니다.

<+49>에서 첫 번째 입력 값이 7보다 크면 <+208>로 분기합니다.

<+208>에서도 터지니까 조심해야합니다.

그럼 지금까지 찾아낸 조건은

1. 입력 값은 정수 두 개

2. 첫 번째 입력 값은 7보다 작거나 같아야한다.

가 되겠습니다.

위의 지뢰들을 무사히 지나오면 <+55>를 만날 수 있습니다.

*rsp를 eax에 옮깁니다.

그리고 rip를 rdx에 옮기네요. rdx의 값은 한 번 확인해봐야겠습니다.

이렇게 생겼습니다.

<+65>에서 (rdx+rax4)를 rax에 저장합니다.

eax가 rax의 하위비트니까 rax도 같은 값을 가지겠죠?

첫 번째 입력 값에 따라서 rax에 들어가게 되는 값은 달라지겠네요.

저는 첫 번째 입력 값으로 2를 넣었기 때문에 *rdx+0x08에 해당하는 0xffffe8a9가 rax로 들어옵니다.

<+69>에서는 rdx와 rax를 계산합니다. 0x555555402b70 + 0xffffffffe8a9 = 0x555555401419

<+72>에서는 연산의 결과로 분기합니다. 0x555555401419가 어딘지 확인해보니

<+166>이네요.

<+166>에선 eax를 0으로 만들고 <+171>에서 <+98>로 분기합니다.

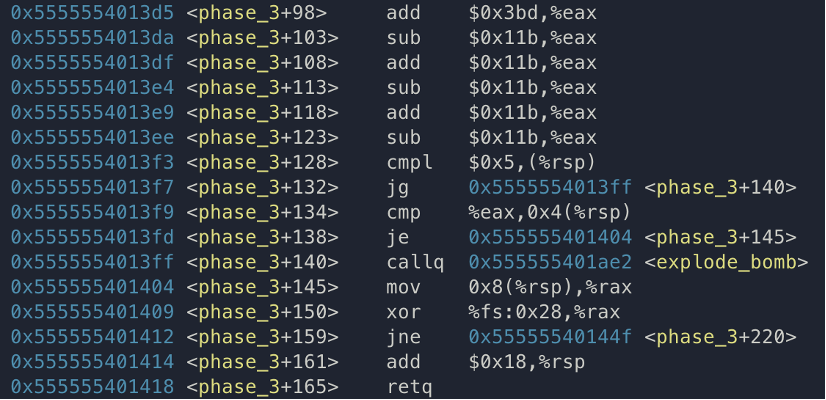
<+98> ~ <+123>에는 이상한 연산들이 있습니다...

눈살이 찌푸려지지만 <+108> ~ <+123>은 다 상쇄돼서 무의미한 연산이었네요.

eax에 0x3bd를 넣고, 0x11b를 뺍니다. 0x3bd - 0x11b = 0x2a2가 eax에 최종적으로 남게 되겠네요.

<+128>에선 첫 번째 입력 값과 5를 비교합니다.

<+132>에서 비교 결과가 더 크면 <+140>으로 분기하고 폭탄이 터지네요.

만약, 첫 번째 입력 값으로 6을 넣었다면 허무했을겁니다. 저는 2를 넣었으니까 다행이네요.

<+134>에서 eax와 두 번째 입력 값을 비교합니다.

<+138>에서 같으면 <+145>로 분기, 다르면 분기하지 못해 터집니다.

그 뒤로 연산은 없고 페이즈가 종료되니까 두 번째 입력 값은 eax인 0x2a2가 되겠네요.

십진수로 계산하기 귀찮아서 변환기를 돌려보니까 674가 나왔습니다.

정답은 2 674입니다.

여기서, 첫 번째 입력 값에 따라서 분기 지점이 다릅니다.

그래서 답은 여러 개가 될 수 있습니다.

확인해보니 모두 <+93> ~ <+128> 중 어딘가로 분기합니다.

그에 따른 연산 결과가 답이 되겠네요.

2 674를 넣으면,

절반 왔다고 기운을 북돋아줍니다.