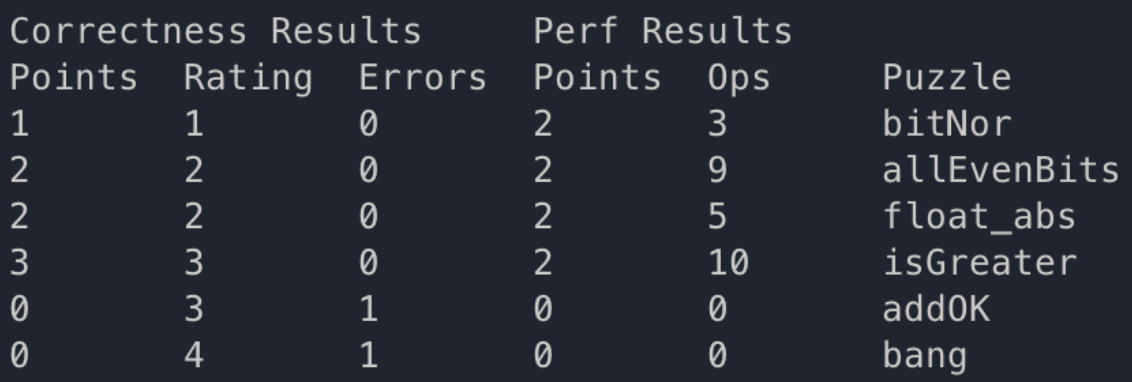
#3. float_abs

/*
 * float_abs - Return bit-level equivalent of absolute value of f for
 *   floating point argument f.
 *   Both the argument and result are passed as unsigned int's, but
 *   they are to be interpreted as the bit-level representations of
 *   single-precision floating point values.
 *   When argument is NaN, return argument..
 *   Legal ops: Any integer/unsigned operations incl. ||, &&. also if, while
 *   Max ops: 10
 *   Rating: 2
 */
unsigned float_abs(unsigned uf) {
  return 2;
}

문제는 위와 같습니다. 이 문제의 경우 조건문, 반복문을 사용 가능하고, 상수 선언의 제약 조건 또한 널널해졌습니다. (기존 상수 선언은 0x00~0xff까지만 가능) 부동 소수점으로 표현된 숫자의 절댓값을 출력하는 문제입니다.

부동 소수점의 경우는 MSB가 sign을 표시하는 비트로, 만약 이 부분이 1이라면 0으로 바꾸어주면 되겠습니다.

이 때 주의해야할 부분은 floating point 표기에 존재하는 NaN(Not a Number)입니다. exp부분이 0000...0으로 이루어져 있고, frac부분이 0x0이 아닌 경우가 이에 해당합니다. 이 경우를 소거해주기 위해 조건문을 사용해야겠네요.

따라서 정답은 아래와 같습니다.

// 3번 풀이


unsigned float_abs(unsigned uf) {
  int check = uf & 0x7f800000;  // exp부분의 비트만 남게 된다.
  if (check == 0x7f800000 && (uf & 0x007fffff)) return uf;
  // exp부분의 비트가 111...1인가? frac부분의 비트가 0이 아닌가? --> 두 경우에 해당하면 NaN
  return uf & 0x7fffffff;
}

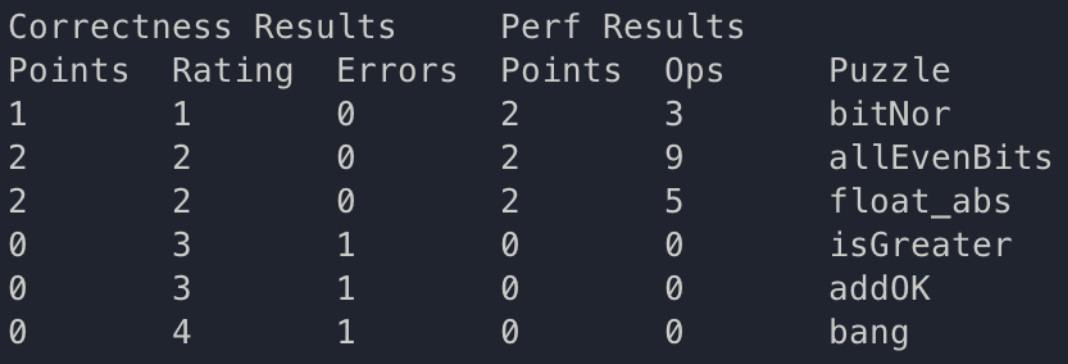
#4. isGreater

/*
 * isGreater - if x > y  then return 1, else return 0
 *   Example: isGreater(4,5) = 0, isGreater(5,4) = 1
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 24
 *   Rating: 3
 */
int isGreater(int x, int y) {
  return 2;
}

문제는 위와 같습니다. x가 y보다 크다면 1을, 그렇지 않다면 0을 리턴합니다.

input은 x, y 둘다 정수이고, 사용 가능한 연산자는 2번 문제와 동일합니다.

우선, 두 수를 비교하기 위해서 두 수의 부호를 살펴보아야 합니다.

만약 두 수의 부호가 다르다면, 부호만 비교해도 됩니다.

만약 두 수의 부호가 같다면, 둘을 뺀 결과값의 부호를 보아야 합니다. (이 때, 오버플로우는 발생하지 않으므로 오버플로우 발생의 경우는 고려하지 않습니다.)

정답은 아래와 같습니다.

// 4번 풀이


int isGreater(int x, int y) {
  int is_diff = x ^ y;
  int sub_sign = (x + ~y);
  return ((is_diff & ~x) | ~(is_diff | sub_sign)) >> 31 & 0x01;
}

압축된 부분이 많아 하나하나 설명드리겠습니다.

1. is_diff: x와 y의 부호비트 xor 연산 (다르다면 1, 같다면 0)

2. sub_sign: x - y의 부호

여기서 2의 보수 표현법으로 -y = (~y) + 1이지만, x = y인 경우 또한 0을 리턴합니다.

즉, x - y >= 1이어야 합니다. 이 식은 x + (~y) + 1 >= 1이고, 양변에 1을 빼주면 x + (~y) >= 0이 됩니다. 이렇게 함으로써 'x가 y보다 클 때에만 1이다.' 라는 반환 조건을 해결할 수 있습니다.

3. 리턴 값

• is_diff & ~x
  두 수의 부호가 다를 때 is_diff의 MSB는 1이 될 것입니다. 만약, x가 음수라면 0을 반환해야 합니다. 여기서 x의 MSB는 1이고, not 연산을 취하게 되면 MSB가 0이 됩니다. 반대로 양수라면 MSB가 1이 될 것입니다. is_diff와 ~x를 and 연산을 취해 x와 y의 부호가 다른 경우를 해결합니다.

• ~(is_diff | sub_sign)
  이 경우는 (~is_diff & ~sub_sign)으로 해석하는 편이 편합니다. 두 수의 부호가 같을 때 is_diff의 MSB는 0이 될 것입니다. 이를 not연산 취하면 1이 됩니다. 그리고 두 수를 뺀 결과가 양수라면 x가 더 큰 경우를 의미합니다. 이 때 sub_sign의 MSB는 0일 것입니다.
  x가 더 큰 경우에 1을 반환하라고 하였으므로 not 연산을 취해 sub_sign의 MSB를 뒤집어줍니다. x가 더 작은 경우에도 위 과정은 동일합니다. (~is_diff & ~sub_sign)에서 not 연산이 반복되므로 이를 간결하게 나타내주기 위해 드모르간의 법칙을 이용해 ~(is_diff | sub_sign)으로 바꾸어 주었습니다. 이러한 방식으로 x와 y의 부호가 같은 경우를 해결합니다.

위의 두 경우를 or 연산자로 이어줍니다. is_diff의 MSB값에 따라 두 경우가 나뉘기 때문입니다. 그리고 지금까지 MSB를 통해 이 문제를 해결해주었으니 반환 값을 양식대로 조정해주어야합니다.

shift right 연산을 이용해 결과값을 31비트만큼 오른쪽으로 밀어줍니다. 여기서 shift right는 arithmetic방식으로 적용이 되기 때문에, MSB가 1인 경우에 0xffffffff라는 결과가 생길 것입니다. 우리가 원하는 값은 1이므로 상위 비트들을 덮어주기 위해 0x01과 and 연산을 취해줍니다.