#5. addOK

/*
 * addOK - Determine if can compute x+y without overflow
 *   Example: addOK(0x80000000,0x80000000) = 0,
 *            addOK(0x80000000,0x70000000) = 1,
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 20
 *   Rating: 3
 */
int addOK(int x, int y) {
  return 2;
}

문제는 위와 같습니다. 두 수를 더했을 때 오버플로우가 발생하는지 확인하는 문제입니다.

2번 문제와 동일한 연산자 제약 조건이네요.

오버플로우는 두 수의 부호가 같을 때, 연산 결과의 부호가 기존 두 수의 부호와 다를 때 발생합니다.

즉, 음수 + 음수를 연산하는데 결과값의 MSB가 0인 경우, 양수 + 양수를 연산하는데 결과값의 MSB가 1인 경우가 이에 해당합니다.

이를 종합한 정답 코드는 아래와 같습니다.

// 5번 풀이


int addOK(int x, int y) {
  return ((x ^ y) | ~(x ^ (x + y))) >> 31 & 0x01;
}

4번과 같은 방식으로 MSB끼리 비교한 후 마지막에 31비트 만큼 shift right, 상위 비트를 제거하기 위해 0x01과 and 연산을 취해주었습니다.

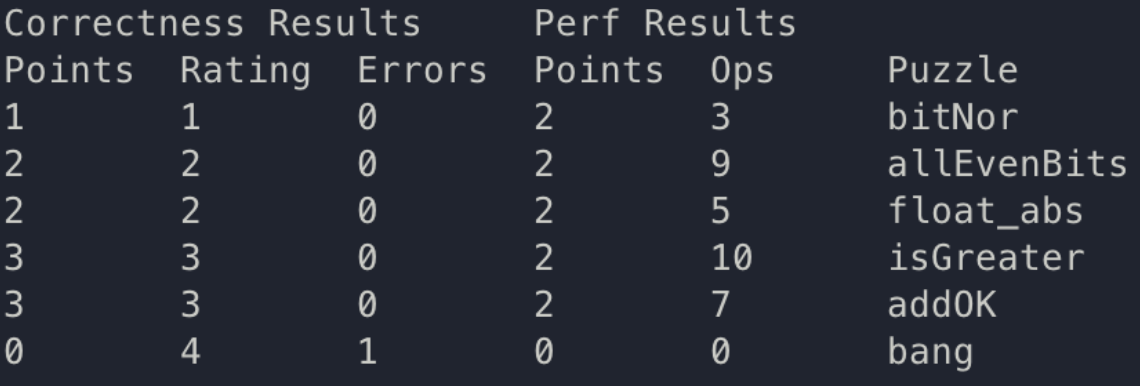
#6. bang

/*
 * bang - Compute !x without using !
 *   Examples: bang(3) = 0, bang(0) = 1
 *   Legal ops: ~ & ^ | + << >>
 *   Max ops: 12
 *   Rating: 4
 */
int bang(int x) {
  return 2;
}

문제는 위와 같습니다. 이 문제는 논리 부정을 논리 부정 연산자 없이 표현하는 것입니다.

사용가능 연산자는 다른 문제들에서 논리 부정만 빠진 정도입니다.

여기서 알고가야 할 것은 0을 제외한 모든 수는 참(1)의 진리값을 가집니다.

따라서, 32개의 비트 중 어떤 하나라도 1이라는 값을 가진다면, 참이라는 것입니다.

이렇게 생각하면 2번과 비슷하게 풀 수 있겠습니다.

비트를 모두 겹쳐 or 연산을 합니다. 여기서 1이 하나라도 존재하면 최종 결과값의 LSB에는 1이 저장이 되겠네요.

정답은 아래와 같습니다.

// 6번 풀이

int bang(int x) {
  x = x | x >> 16;
  x = x | x >> 8;
  x = x | x >> 4;
  x = x | x >> 2;
  x = x | x >> 1;
  return (x & 0x01) ^ 0x01;
}

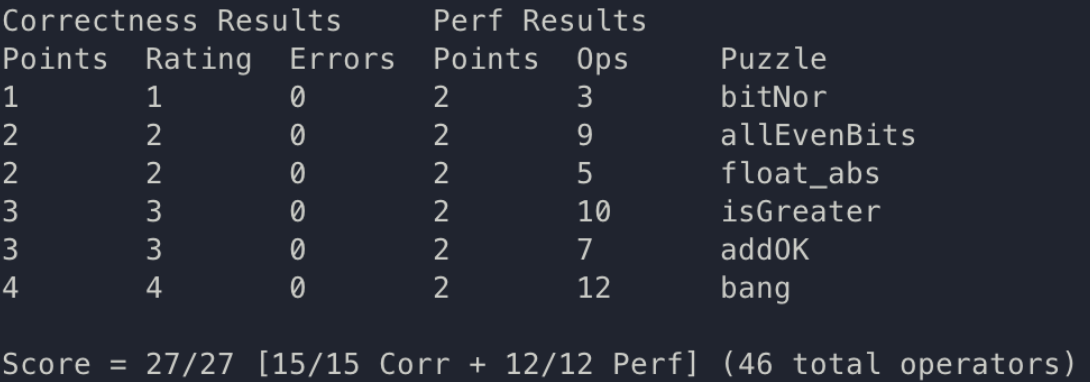
이렇게 DataLab 과제 풀이가 끝났습니다 🎉