이것이 코딩테스트다 with 파이썬 | 구현 ②

---

실전문제

1) 왕실의 나이트 🏹

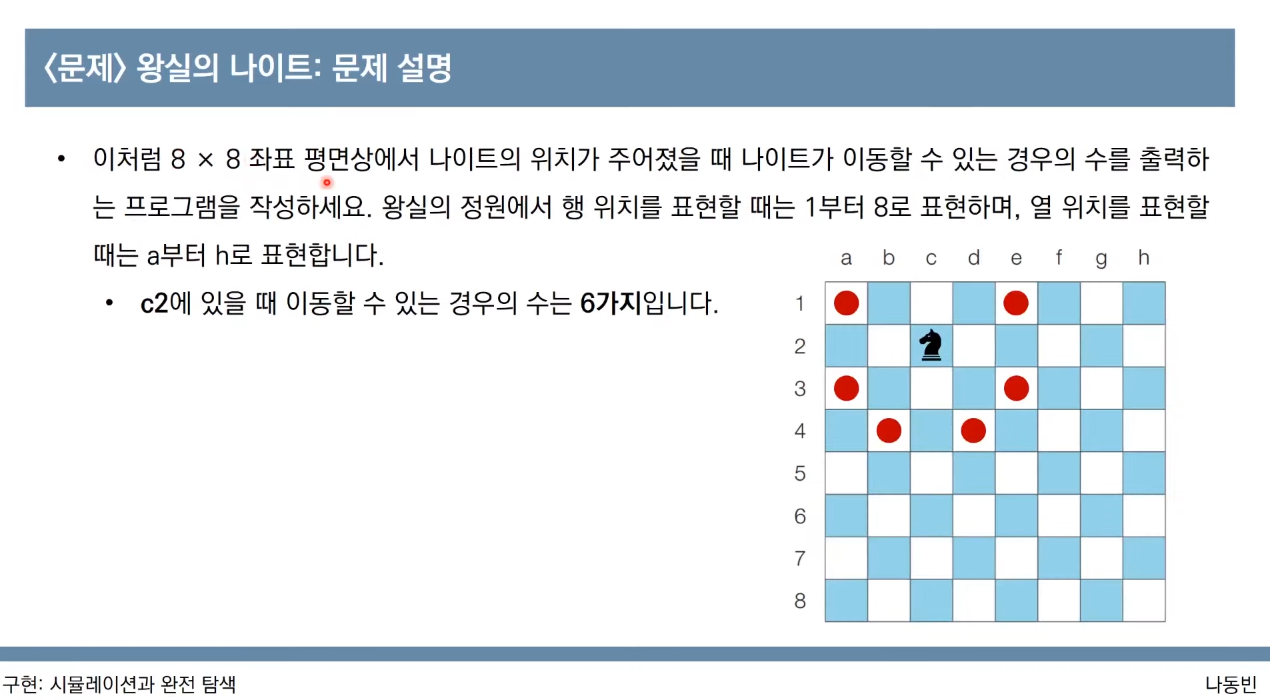
이 문제또한 설명이 길기 때문에 유튜브 강의로 나와있는 문제설명을 캡쳐해서 수록했다.
나동빈의 유튜브 강의 바로 가기


(입력) : 좌표를 나타내는 문자와 숫자를 입력한다.
(출력) : 입력된 좌표에서 나이트가 이동할 수 있는 경우의 수

내가 문제풀면서 떠올린 사고 흐름🤨

전에 풀었던 상하좌우 문제랑 결이 비슷한 것같다.

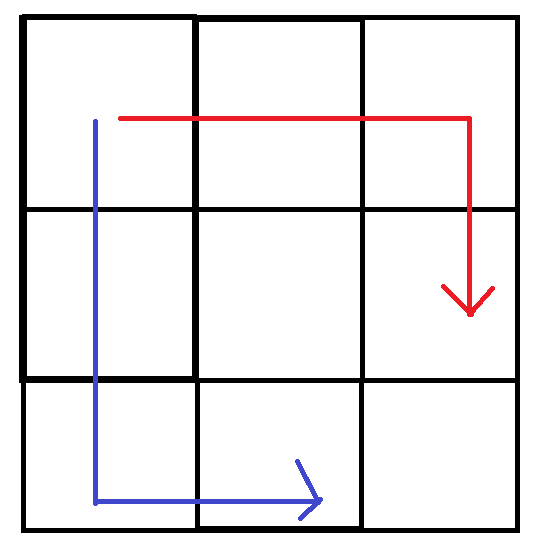
1. 수평으로 두 칸 이동 뒤에 수직으로 한칸 이동
2. 수직으로 두 칸 이동 뒤에 수평으로 한칸 이동

1번을 만족하려면 최소한 현 좌표 포함 2X3만큼의 여유공간이 있어야한다.
2번을 만족하려면 최소한 현 좌표 포함 3X2만큼의 여유공간이 있어야한다.
1,2번을 만족하려면 최소한 현 좌표 포함 3X3만큼의 여유공간이 있어야한다.

a : 오른쪽으로 수평 2칸/1칸
b : 왼쪽으로 수평 1칸/오른쪽으로 수평 2칸/1칸
c~f : 왼/오른쪽으로 수평 2칸/1칸
g : 왼쪽으로 수평 2칸/오른쪽으로 수평 1칸
h : 왼쪽으로 수평 2칸

---

1 : 아래로 수직 2칸/1칸
2 : 아래로 수직 2칸/1칸 or 위로 수직 1칸
3~6 : 아래로 수직 2칸/1칸 or 위로 수직 1칸/2칸
7 : 아래로 수직 1칸 or 위로 수직1칸/2칸
8 : 위로 수직 1칸/2칸

👇 답지를 보기 전 작성한 코드

coor=input() #좌표

coor_row=coor[0] #열 (a~h)
coor_col=coor[1] #행 (1~8)
ct=0

row=['a','b','c','d','e','f','g','h']
col=[1,2,3,4,5,6,7,8]

#right_row1=[1,1,1,1,1,1,1,0]
#right_row2 = [2,2,2,2,2,2,0,0]

#left_row1=[0,-1,-1,-1,-1,-1,-1,-1]
#left_row2 =[0,0,-2,-2,-2,-2,-2,-2]

#down_col1=[1,1,1,1,1,1,1,0]
#down_col2 = [2,2,2,2,2,2,1,0]

#up_col1=[0,-1,-1,-1,-1,-1,-1,-1]
#up_col2=[0,0,-2,-2,-2,-2,-2,-2]

for i in row:
  if coor_row==i: #(a~h)
    for j in col:
      if int(coor_col)==j: #(1~8)
        if not i in ['a','b','g','h']:
          if not j in [1,2,7,8]:
            ct=8
          else:
            if j==1:
              ct=4
            elif j==2:
              ct=6
            elif j==7:
              ct=6
            elif j==8:
              ct=4
        else:
          if i=='a' or i=='h':
            if not j in [1,2,7,8]:
              ct=4
            else:
              if j==1:
                ct=2
              elif j==2:
                ct=3
              elif j==7:
                ct=3
              elif j==8:
                ct=2
          else:
            if not j in [1,2,7,8]:
              ct=4
            else:
              if j==1:
                ct=3
              elif j==2:
                ct=4
              elif j==7:
                ct=4
              elif j==8:
                ct=3
        break
print(ct)    
    

예시 출력과 맞게 풀긴했지만 경우에 맞게 다 센건지, 그리고 if문이 너무 길어서 불안하기도 했다.
이렇게 코드가 무식하게 길 수 없을 것같아..
아니나 다를까, 답안 예시는 내가 길게 써놓은 코드가 무색하게 간결했다.

📌답안 예시를 본 후 피드백
① 주석 처리해놓은 right_row1, up_col1 ... 얘네들을 경우의 수로 하나하나 볼 것이 아니라 튜플로 묶었으면 편리했다.
② 계산 후, 좌표가 8X8 좌표 평면 상에 존재하는지만 체크하면 더 코드가 간결했다.

👇 피드백 후 코드

coor=input() #좌표
row=int(coor[1]) 
col=int(ord(coor[0]))-int(ord('a'))+1 
#a:1, b:2 ...
steps=[(-2,-1),(-1,-2),(1,-2),(2,-1),(2,1),(1,2),(-1,2),(-2,1)]
ct=0
for step in steps:
  next_row=row+step[0]
  next_column=col+step[1]
  if next_row >=1 and next_row<=8 and next_column>=1 and next_column<=8:
    ct+=1
print(ct)

개인적으로 유니코드 반환 함수인 ord를 써서 알파벳을 1~8의 형태로 변환해서 좌표 계산하는 것이 인상깊었다. 다음에 행렬 계산할 때 비슷한 흐름의 문제가 있다면 써먹어도 좋을 것같음
튜플을 사용하거나, x와 y좌표의 방향을 따로 리스트화 해서 만들거나 하는 방법도 기억할 것!