📝이 포스트는 Parameter 개수와 출력 이미지 크기를 계산하는 법에 대해 알아보겠습니다.

신경망 모델들을 공부하거나 관련 논문들을 읽다보면 합성곱을 거친 이미지의 크기가 어떻게 되는지, 파라미터 개수가 어떻게 계산되는지 헷갈리는 경우가 있습니다.

출력 이미지 크기 계산

Convolution을 적용한 출력 이미지 크기 계산하는 방법은

를 따릅니다.
필터의 보폭($Stride)$가 클수록 출력 이미지의 크기는 줄어듭니다.

파라미터 개수 계산

파라미터 개수를 계산할 때 어떤 Layer인지에 따라 계산하는 법이 다릅니다.
Convolutional Layer의 경우와 Fully Connected Layer의 경우가 있습니다.

• Convolutional Layer

  

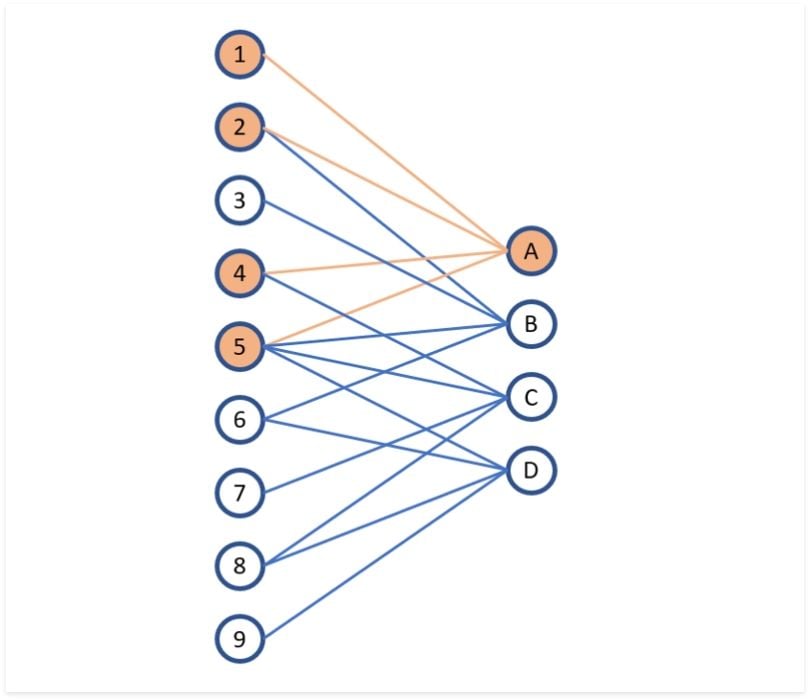
  Convolutional Layer는 필터가 입력 데이터 위로 이동하면서 합성곱 연산을 수행합니다.
  따라서 합성곱 층의 파라미터 개수는 필터의 크기 & 필터의 채널 수 & 필터의 개수에 의존합니다.

  convolution 적용할 필터의 한 변의 크기 : $F_{length}$
  convolution 입력 채널 수 : $C$
  출력 채널 개수(=다음 층의 채널 수) : $N$
  $bias$ : $1$

  $parameter = (F_{length} \times F_{length} \times C) \times N + 1 \times N$

  로 표현할 수 있습니다.

  $(F_{length} \times F_{length} \times C)$ 는 적용할 필터의 가로, 세로, 채널 즉 x, y, z축이 되겠고 이 형식의 필터를 몇 개($N$) 적용할 것인지 로 이해할 수 있습니다.
  $1 \times N$ 는 Bias 를 표현한 것입니다.

  위 식을 $N$으로 결합법칙을 적용하면

  ${parameter} = (F_{length} \times F_{length} \times C + 1) \times N$

  으로 이전 식보다 간략하게 표현할 수 있습니다.
  

• Fully Connected Layer

  

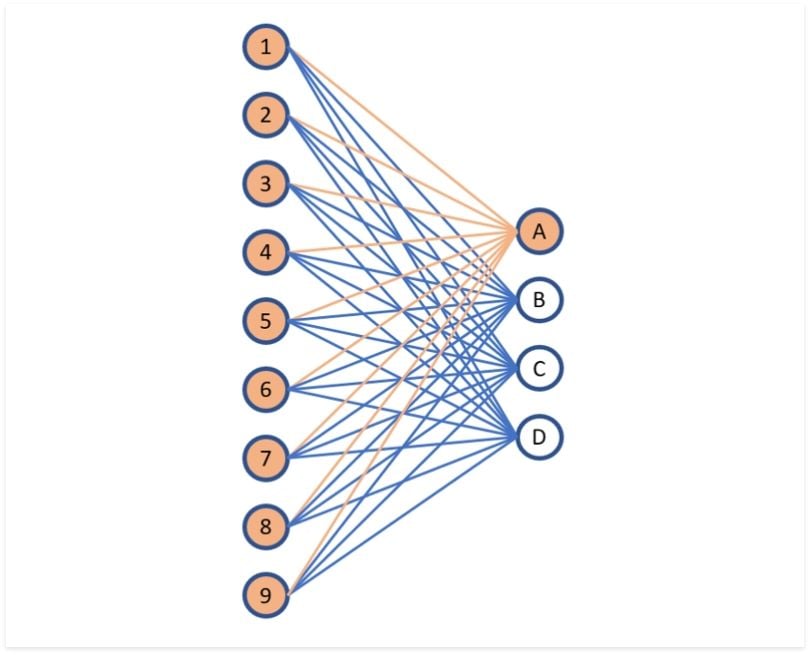
  • 직전 층이 Convolutional Layer일 경우

    직전층이 Convolutional Layer니깐 Filter의 영향을 받을 것입니다.
    따라서 필터의 크기 & 필터의 채널 수 & 필터의 개수에 의존합니다.
    그리고 필터에 관한 파라미터에 Fully-connected Layer의 노드 수를 곱하면 총 파라미터의 개수를 구할 수 있습니다.
    $I_{length}$ : 입력 이미지의 한 변의 크기
    $I_n$ : 입력 이미지의 수
    $I_c$ : 입력 이미지의 채널 수
    $N_{node}$ : 현재 층의 노드(뉴런) 수
    $bias$ : 1
    $parameter = (I_{length} \times I_{length} \times I_c \times I_n) \times N_{node} + 1 \times N_{node}$
    
    
    

  • 직전 층이 Fully-connected Layer일 경우

    현재 층의 노드(뉴런) 수 : $FC_i$
    직전 층의 노드(뉴런) 수 : $FC_{i-1}$
    $bias$ : $1$
    $N_{parameter} = FC_{i-1} \times FC_i + 1 \times FC_i$
    쉽게 생각해보면 fully connected 를 해석해보면 모든 노드가 연결되었을 경우니깐 단순히 모든 노드들이 연결되있는 상황을 계산하면 됩니다.