[논문리뷰] Batch Normalization : Accelerating Deep Network Training by Reducing Internal Covariate Shift
Machine Learning

📝 이 글에서 우리가 흔히 알고 무의식적으로 사용하는
배치 정규화(Batch Normalization)에 대한 논문을 알아보겠습니다.
이 논문이 나오기 이전 과거에 배치단위 학습을 시키는 개념이 있었습니다.
📗배치(Batch)란?
- 데이터를 실시간(real time)으로 처리하는게 아니라, 일괄적으로 모아서 처리하는 작업을 의미한다.
- 배치단위 학습의 장점은
- 학습 속도 향상 : mini-batch라는 작은 데이터 그룹에 대해 weight update를 할 수 있었습니다.
- 메모리 효율성 : 예를 들어 RAM이나 GPU에 한 번에 60,000장을 한꺼번에 학습한다면 과한 적재로 과부화가 올 수 있습니다...
그래서 32 or 64장 (or 2의 거듭제곱 수) 씩 끊어서 학습을 하여 메모리에 로드되는 데이터양을 통재하여 효율적으로 학습할 수 있었습니다. - 확률적 경사하강법(SGD): Batch별 학습은 확률적 경사하강법(Stochastic Gradient Descent, SGD)와 함께 사용됩니다. SGD는 각 Batch에 대해 weight update를 수행하므로 더 빠르게 수렴할 수 있고, Local Minimum에 갇히지 않을 가능성이 높습니다.
하지만 배치단위로 학습을 하게 되면 발생하는 문제점이 있었습니다💦
이것이 바로 논문에서 다루는 주요한 학습이 불안정한 이유입니다.
📈 Internal Covaria Shift
📕 Internal Covariate Shift란?
- 한국말로, 내부 공변량 변화이다. 의미는 학습 과정에서 계층 별로 입력의 데이터 분포가 달라지는 현상을 뜻한다.
그림으로 이해를 해보면 아래와 같습니다.
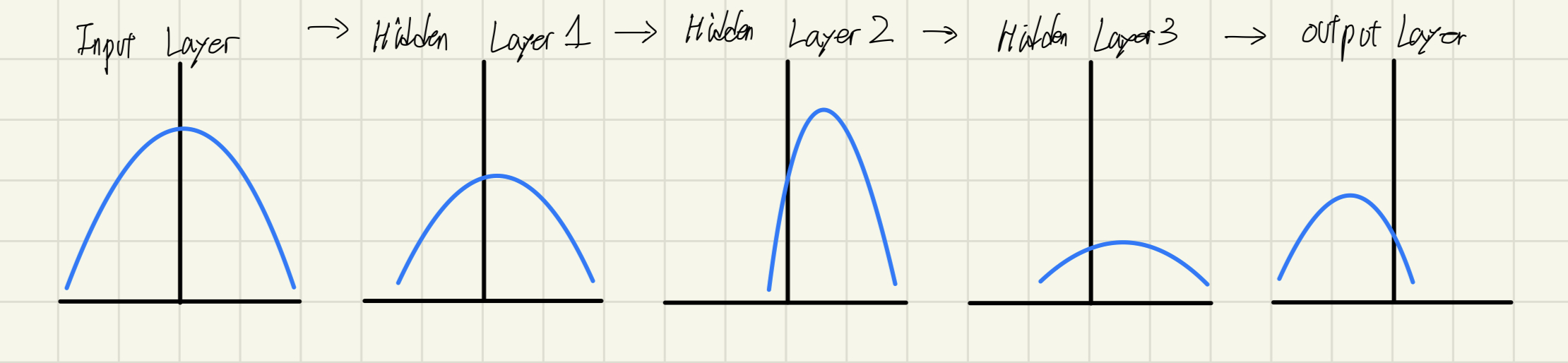
매 Layer마다 정규분포가 다른 형태의 표준정규분포곡선을 보입니다.
❗️Internal Covariate Shift가 Layer간에도 나타나는 현상이지만, Batch 간에서도 나타나는 현상입니다.
- Batch 묶음 단위 간의 데이터 불균형이 존재하기 때문입니다. 1반부터 12반까지 반평균이 다 같을 수 있을까요?? 답은 아니죠
Internal Covariate Shift의 존재를 코드로 살펴보겠습니다.
import numpy as np
list_xy = [] # xy 좌표로 표현할 2차원 난수 배열
for i in range(2**10):
x = np.random.randint(-100,100)
y = np.random.randint(-100,100)
list_xy.append([x, y])
list_xy = np.array(list_xy)print(list_xy)🖨️결과
[[ 37 -77]
[-16 -38]
[-33 61]
...
[ 43 76]
[ 65 41]
[-61 -45]]그리고 이어서
batch_size = 32 # 배치 크기
num_batches = len(list_xy) // batch_size
batch_mean = [] # 배치 당 평균
batch_var = [] # 배치 당 분산
for i in range(num_batches):
# 배치 단위로 데이터 추출
batch = list_xy[i * batch_size: (i + 1) * batch_size]
# 평균 계산
batch_mean.append(np.mean(batch, axis=0))
# 분산 계산
batch_var.append(np.var(batch, axis=0))
# 결과 출력
batch_mean = np.array(batch_mean)
batch_var = np.array(batch_var)print('shape : ', batch_mean.shape)
print('centroid :\n', batch_mean) # 한 배치의 평균이 곧 그 배치의 무게중심(centroid)을 뜻한다.🖨️결과
shape : (32, 2)
centroid :
[[ 12.96875 -1.8125 ]
[ 4.75 -8.90625]
[ -4.65625 20.28125]
...
[ -5.875 -9.28125]
[ 17.4375 -4.59375]
[ 1.21875 0.6875 ]]수치로 보아서 이해가 어려울 수 있어 그래프를 그려보겠습니다.
import matplotlib.pyplot as plt
x = batch_mean[:, 0] # x축 데이터 (index=0)
y = batch_mean[:, 1] # y축 데이터 (index=1)
plt.scatter(x, y) # scatter 그래프 그리기
plt.show() # 그래프 출력🖨️결과
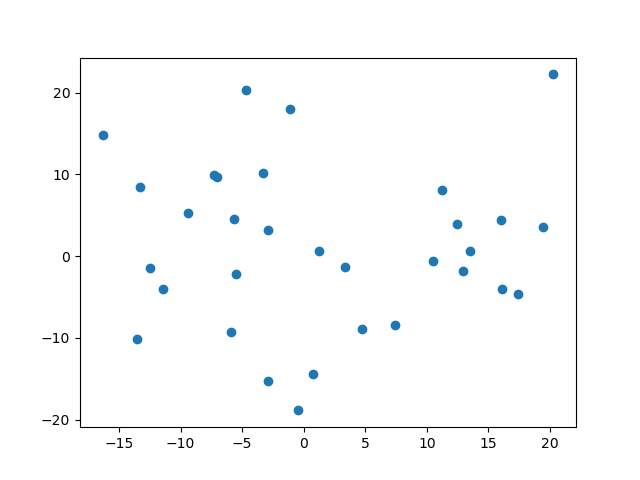
이 점들이 각 mini-batch(size=32)의 Centroid(무게중심=평균)를 뜻합니다.
이 산점도를 봤을 때 산포도가 넓은 것을 확인할 수 있는데요, 이말은 즉, 배치별로 Internal Covariate Shift가 존재함을 뜻합니다.
⚠️ Internal Covariate Shift를 해결할 방법이 있었습니다.
그 방법은 바로 weight initialization과 learning rate를 줄여 해결하는 방법이였는데요.
- weight initialization한다는 것은 어려운 일이라고 생각합니다. 저 역시 난수를 통해 weight initialization을 수행하고, back propagation을 통해 gradient로 weight를 update하는 방법뿐이라고 생각하는데요...
- ❗️ 문제는 learning rate를 줄이는 방법입니다.
그 문제는 바로 Local Minimum에 갇힐 수 있다는 위험입니다.
Gradient는 미분값 즉 변화량을 의미하고, learning rate를 낮춘다면 Vanishing Gradient 문제를 겪으면서 local minimum에 갇혀 weight들이 update되지 못하여 Global Minimum에 수렴하지 못하는 상황이 발생할 수 있다는 것입니다.
이 방법들 말고 Whitening이라는 방법이 있습니다. 논문에서도 언급이 되는데요.
📕Whitening이란?
- 데이터의 특성을 변환하여 데이터의 특정 통계적 특징을 제거하고, 데이터의 상관 관계를 줄이는 전처리 기법입니다.
공분산 행렬을 이용하여 대각 행렬의 성분이 1이 되고 uncorrelated시키는 방법입니다.
❗️하지만 covariance matrix의 연산과 inverse 연산이 요구되어 계산 복잡도가 증가하여 메모리 효율성이 떨어지게 됩니다.
이 문제를 해결하기 위해 나온 것이 이 논문에서 다루는
📈 Batch Normalization
입니다.
- Whitening은 평균과 분산을 학습시키는 과정이 Neural Network를 학습시키는 과정과 병행되지 않지만,
Batch Normalization은 평균과 분산을 학습시키는 과정이 Neural Network 학습과 병행된다는 점이다. - Batch Normalization은 학습 과정에서 각 Batch 단위 별로 데이터가 다양한 분포를 가지더라도 각 Batch별로 평균과 분산을 이용해 Normalization하여 Internal Covariate Shift를 완화시켜 학습 과정의 안정성을 향상시킵니다.
혹시 Normalization을 모르시는 분들을 위해 설명 짚고 넘어가겠습니다.
📗Normalization이란?
- 평균(mean) = 0, 분산(variance) = 1이 될 수 있도록 하고 전처리를 수행하는 것을 뜻한다.
- 이렇게 변환하는 이유는 학습 속도가 향상되기 때문이다. (Vanishing Gradient 회피, local minimum 회피 등등...)
- 예를 들어 이미지의 픽셀값 는 의 범위를 가지게 된다면 정규화를 수행하여 나오는 (정규화된 )은
의 범위를 가질 것이다.
🏅배치 정규화의 장점
- 학습 속도를 향상시킬 수 있습니다.
배치 정규화 수행 시 기존 모델보다 14배 적은 학습 횟수로 동일한 정확도를 보여줄 수 있다고 합니다.
즉, 적은 epoch으로도 모델의 학습이 빠르게 수렴한다는 것입니다. - 가중치 초기화(weight initializaiton)에 대한 민감도를 감소시킵니다.
- 모델의 일반화(regularization) 효과가 있습니다.
논문에서 배치정규화는 학습 단계와 추론 단계로 나눈다고 합니다.
Train Batch Normalization

논문의 "3. Normalization via Mini-Batch Statistics"의 Algorithm 1.
- mini-batch 구하기 ()
주로 사이즈 은 2의 제곱수로 정합니다.
mini-batch(=input) : 한 번 학습시키는데 소요될 데이터 수. - mini-batch mean() 구하기
- mini-batch variance() 구하기
- Normalization
- 저는 "(epsilon) 은 무엇일까??"라는 의문이 생겼습니다..🤔
- 그래서 찾아보니 (standard deviation)이 0에 수렴하면 divide by zero 문제에 국면하게 됩니다.
은 연산을 수행할 때 divide by zero문제가 생기지 않게 안전성을 더하기 위해서 첨가하는 아주 작은 크기의 상수라고 보면 됩니다.
- 그래서 찾아보니 (standard deviation)이 0에 수렴하면 divide by zero 문제에 국면하게 됩니다.
- Scale & Shift: scaling
: shift
- 이번엔 " 𝛾, β가 왜 수식에 붙어있는거지? "라는 의문이 생겼습니다..🤔
- activation layer와 batch normalization을 생각해보면
𝛾, β가 수식에 존재하는 이유를 찾을 수 있다.
hidden layer의 activation layer에 sigmoid, ReLU, tanh가 올 수 있다.
ReLU가 적용된 상황을 생각해보자!
ReLU가 적용된다면 한 배치 내의 데이터 중에서 음수에 해당하는 부분들이 0으로 변하게 됩니다. 데이터 손실로 이어지죠💦
sigmoid, tanh는 데이터를 계속 정규화하게 되면 non-linearity를 잃게 되는 문제가 있습니다.
따라서 𝛾를 곱하고, β를 더하여 ReLU가 적용되더라도 정규화 결과의 음수부분이 0으로 데이터 유실과 non-linearity를 유지하게 해줍니다.
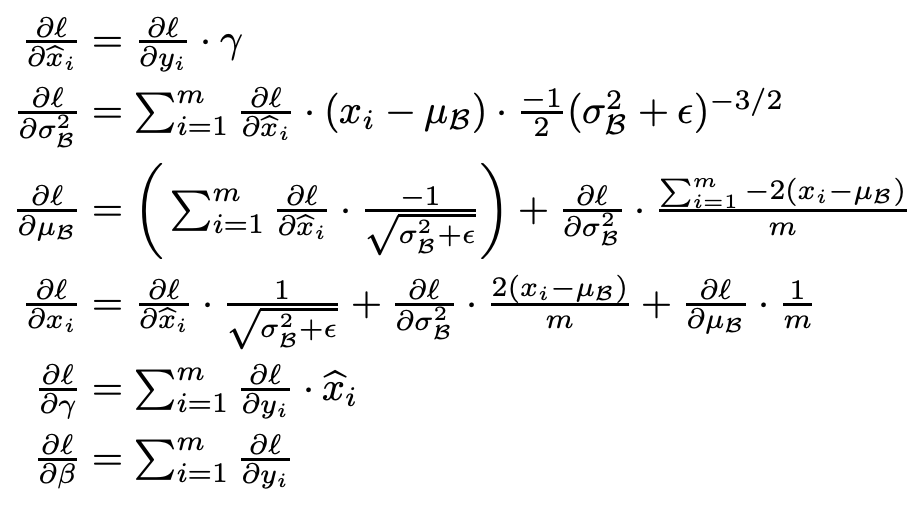
논문에서 chain rule을 이용해 와 를 BackPropagation하여 update하는 내용이다.
gamma와 beta는 학습 가능한 매개변수이고, BackPropagation 과정을 통해 Neural Network Model이 자동으로 학습합니다. 이를 통해 모델이 input data의 분포를 적절하게 조정하고, 학습을 안정화시키는 데 도움을 줍니다.
- activation layer와 batch normalization을 생각해보면
❗️ activation function과 batch normalization의 "순서"가 명확히 정의되어 있지는 않지만
일반적으로 batch normalization 후에 activation function을 활용하는게 더 성능이 잘 나왔다고 한다.
(추후 더 논문으로 알아볼 예정)
Inference Batch Normalization
" Inference? 무슨 뜻이지?😅 "
- Inference(추론)단계란 모델이 학습한 결과를 evaluate하기 위해 새로운 데이터 (test dataset)에 모델을 적용하는 단계입니다

1 ~ 6까지 step은 Train Batch Normalization에서 했던 과정입니다.
1. : training할 Batch Normalization Network를 구성.
2. for do : k(# of activations) activation 개수만큼 반복 학습( 1 epoch).
3. Add transformation to : Batch Normalization Network객체를 Batch Normalizaion 하여 y에 할당.
4. Modyfy each layer in with input to take instead : 다음레이어의 input x에 학습된 y를 할당.
5. end for : for loop 종료
6. Train to optimize the parameters : 만들어진 모델로 Network 학습.
7. // Inference BN network with frozen parameters : parameter들을 frozen시킨 상태에서 inference Batch Normalization Network 생성
8. for do : activation 개수(K)만큼 반복
9. //For clarity, : 각 값들 할당
10. Process multiple training mini-batches , each of size , and average over them:
: 각 미니배치의 평균()들의 평균()을 구하고, 분산의 평균()에 이는 추론 단계에서 전체 데이터셋의 평균으로 사용됩니다.
11. In , replace the transform with
에서는 변환 을 로 대체합니다. 는 추론 단계에서 계산된 평균, 는 계산된 분산입니다.
☑️ 즉 Inference에서는 Train에서 구한 mini-batch의 평균들의 평균을 구하고,
Inference에서 분산은 Train에서 구한 분산의 평균을 구하고 을 곱해줍니다.
이러한 과정을 통해 추론 단계에서는 학습된 평균과 분산을 사용하여 입력 데이터를 정규화하고, 배치 정규화의 변환을 적용합니다.
이는 추론 단계에서 모델의 예측을 수행할 때 일관된 정규화를 보장하고, 학습 단계에서 배운 가중치와 매개변수를 재사용할 수 있도록 도와줍니다.
참고로 Inference에서는 배치단위로 evaluate하지 않습니다.
이 이후로는 Batch Normalization의 실험적 증명이 나옵니다.
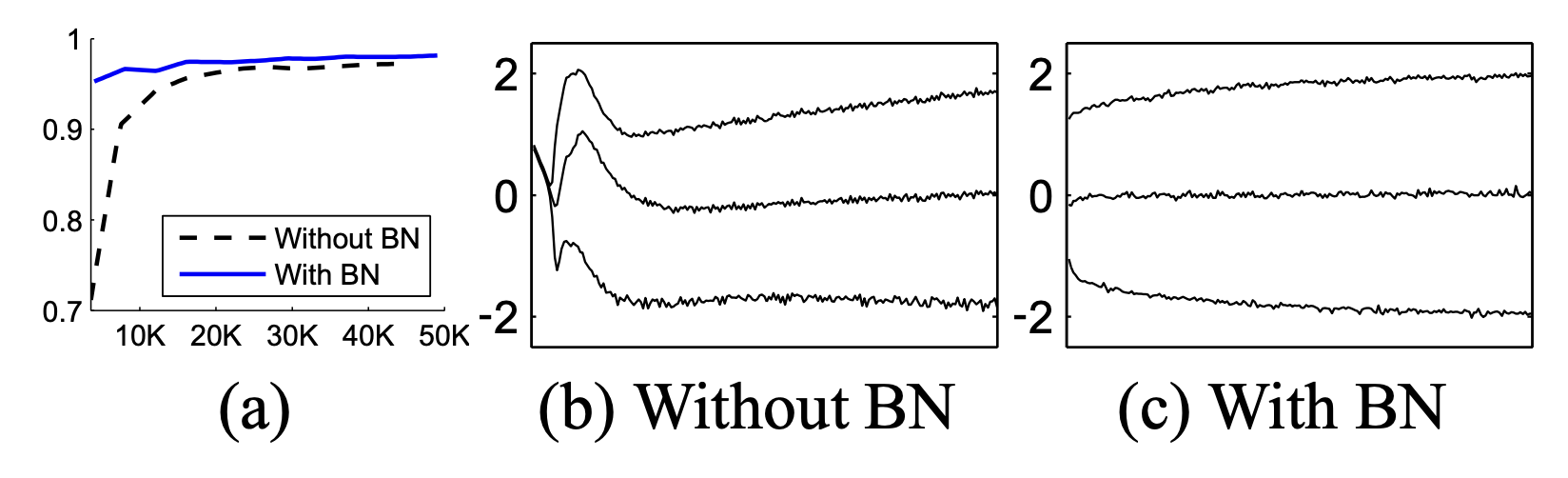
이렇게 하여
Batch Normalization : Accelerating Deep Network Training by Reducing Internal Covariate Shift
논문 리뷰를 마치도록 하겠습니다💯
글을 너무 꼼꼼하게 잘 써주셔서 술술 읽게 되네요~!
자세한 설명 감사합니다🙏🏻