재귀

• 재귀함수 : 함수 내에서 자기 자신 함수를 다시 호출하는 함수
• 재귀함수를 활용하면, 코드를 좀 더 가독성 있고, 짧게 쓸 수 있는 장점이 있다.
  
  

재귀를 이용한 예제 1 - 팩토리얼

[문제]
0보다 크거나 같은 정수 N이 주어진다. 이때, N!을 출력하는 프로그램을 작성하시오.


[입력]
첫쨰 줄에 정수 $N(0\le N \le12)$가 주어진다.


[출력]
첫째 줄에 N!을 출력한다.

예제 입력 1	예제 출력 1
10	3628800

예제 입력 2	예제 출력 2
0	1

문제설명

고등학교 수학시간에 배운 $N!$을 구하는 것이다.

N! = N * (N-1) * (N-2) * . . . * 2 * 1

• $5 factorial = 5! = 5*4*3*2*1$을 구하기 위해서 재귀함수를 이용할 수 있다.

• 팩토리얼을 구하기 위한 함수 순서는 다음과 같다.
  1) n의 값을 팩토리얼 함수의 입력으로 받는다.
  2) n의 값이 10이라면 1을 함수의 반환값으로 반환하고, 프로그램을 종료한다.
  3) n-1의 값을 팩토리얼 함수에 전달하여 1)을 호출한다
  4) 2)에서 얻은 결괏값과 n을 곱한 값을 함수의 반환값으로 반환한다.

  

• 순서 2)와 같이 $n$이 1이라면 더 이상 자기 자신을 호출하지 않고 프로그램을 종료하는 시점을 적어준 것이 포인트이다.
  
  

해답코드

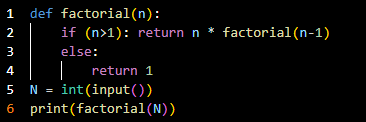
• 코드라인 1~4에서 factorial 함수를 정의했고,
• 코드라인 6에서 factorial(5) 함수를 실행한다.

factorial(5)는 코드라인 2에 의해 5는 1보다 크기 때문에 5 * factorial(4)가 실행되고,
factorial(4)는 코드라인 2에 의해 5는 1보다 크기 때문에 5 * factorial(3)가 실행되고,
factorial(3)는 코드라인 2에 의해 5는 1보다 크기 때문에 5 * factorial(2)가 실행되고,
factorial(2)는 코드라인 2에 의해 5는 1보다 크기 때문에 5 * factorial(1)가 실행되고,
factorial(1)은 코드라인 1에 의해 1 값을 반환한다.

• 다시 거꾸로 올라가 보면,

factorial(1)은 1을 반환했으므로
factorial(2)는 2 * factorial(1)은 2가 되고
factorial(3)은 3 * factorial(2)는 6이 되고
factorial(4)은 3 * factorial(3)는 24이 되고
factorial(5)은 3 * factorial(4)는120이 된다.

재귀를 이용한 예제 2 - 하노이 탑 이동 순서

[문제]
세 개의 장대가 있고 첫 번째 장대에는 반경이 서로 다른 n개의 원판이 쌓여 있다. 각 원판은 반경이 큰 순서대로 쌓여있다. 이제 수도승들이 다음 규칙에 따라 첫 번째 장대에서 세 번째 장대로 옮기려 한다.

1. 한 번에 한 개의 원판만을 다른 탑으로 옮길 수 있다.
2. 쌓아 놓은 원판은 항상 위의 것이 아래의 것보다 작아야 한다.

이 작업을 수행하는데 필요한 이동 순서를 출력하는 프로그램을 작성하라. 단, 이동 횟수는 최소가 되어야 한다.

아래 그림은 원판이 5개인 경우의 예시이다.

[입력]
첫째 줄에 첫 번째 장대에 쌓인 원판의 개수 $N(1 \le N \le 20)$이 주어진다.


[출력]
첫째 줄에 옮긴 횟수 K를 출력한다.

두 번째 줄부터 수행 과정을 출력한다. 두 번째 줄부터 K개의 줄에 걸쳐 두 정수 A B를 빈칸을 사이에 두고 출력하는데, 이는 A번째 탑의 가장 위에 있는 원판을 B번째 탑의 가장 위에 옮긴다는 뜻이다.

예제 입력 1	예제 출력 1
3	7
	1 3
	1 2
	3 2
	1 3
	2 1
	2 3
	1 3

문제설명

3개의 장대가 있고, 첫 번째 장대에는 서로 다른 n개의 원판이 쌓여있다.

1. 한 번에 한 개의 원판만을 다른 탑으로 옮길 수 있다.
2. 쌓아 놓은 원판은 항상 위의 것이 아래의 것보다 작아야 한다.

2가지 규칙을 지키며 첫 번째 장대에서 세 번째 장대로 원판을 전부 옮기면 되는 문제이다. 이때 원판이 이동하는 장대를 출력하자.

• 재귀함수를 이해하기 위한 예제이니 문제의 로직을 먼저 보자.

<예제 1>

2개의 원판을 첫 번째 장대에서 세 번째 장대로 옮기기 위해서

1) 원판 1은 첫 번째 장판에서 두 번째 장판으로 이동한다.

2) 원판 2는 첫 번째 장판에서 세 번째 장판으로 이동한다.

3) 원판 1은 두 번째 장판에서 세 번째 장판으로 이동한다.

<예제 2>

3개의 원판을 첫 번째 장대에서 세 번째 장대로 옮기기 위해서

1)

2)

3)

4)

5)

6)

7)

• 첫 번째 예제와 두 번째 예제에는 공통점이 있다.
• 원판을 옮기기 위해서

1) 가장 큰 원판 n은 맨 밑에 있어야 하므로 원판 n-1개를 첫 번째 장대에서 두 번째 장대로 옮긴다.

2) 원판 n을 첫 번째 장대에서 세 번째 장대로 옮긴다.

3) 원판 n-1개를 두 번째 장대에서 세 번째 장대로 옮긴다.

• 이 3가지 규칙을 통해 원판을 옮기는 것은 재귀적 알고리즘을 이용한다면 쉽게 구현할 수 있다.
  
  

해답코드

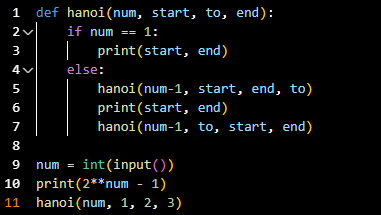
• 코드라인 1: 재귀함수로 현재 이동시킬 원판 num과 원판의 장대의 시작 위치=start, 중간 위치=to, 마지막 위치=end를 함수의 인자로 받는다.
• 코드라인 2~3: 원판 num이 1이라면 start에서 end로 이동을 출력해준다.
  (원판 n을 마지막 장대로 이동. 두번째 예제 7) 부분)
• 코드라인 4: 원판 num이 1이 아니라면
  • 코드라인 5: n-1개의 원판을 start에서 end를 거쳐 to의 장대로 이동시킨다.
    (두 번째 예제 3) 부분)
  • 코드라인 6: 원판 num을 start에서 end로 이동을 출력해준다.
    (두 번째 예제 4) 부분)
  • 코드라인 7: n-1개의 원판을 to부터 시작해서 start를 거쳐 end로 이동시킨다.
    (두 번째 예제 5)~6) 부분)
• 코드라인 10: 원판을 옮겨야 하는 총 횟수는 $2^n-1$이 된다.
  (재귀함수가 $2^n$으로 자신을 호출하며, num==1일 때는 한번 호출됐으므로 -1을 해주면 $2^n-1$이 된다.)
• 코드라인 11: 하노이 재귀함수의 실행값을 출력한다.
  
  

재귀를 이용한 예제 3 - 파이프 옮기기 1

[문제]
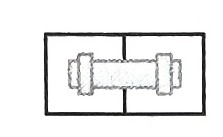
유현이가 새 집으로 이사했다. 새 집의 크기는 N X N의 격자판으로 나타낼 수 있고, 1 X 1 크기의 정사각형 칸으로 나누어져 있다. 각각의 칸은 ($r, c$)로 나타낼 수 있다. 여기서 $r$은 행의 번호, $c$는 열의 번호이고, 행과 열의 번호는 1부터 시작한다. 각각의 칸은 빈칸이거나 벽이다.

오늘은 집 수리를 위해서 파이프 하나를 옮기려고 한다. 파이프는 아래와 같은 형태이고, 2개의 연속된 칸을 차지하는 크기이다.

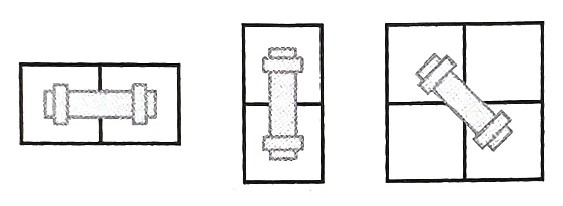
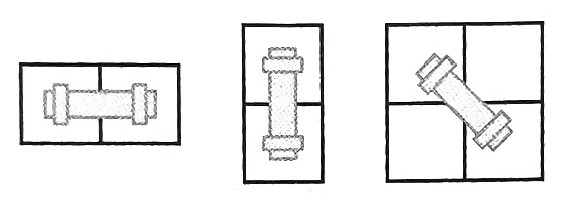
파이프는 회전시킬 수 있으며, 아래와 같이 3가지 방향이 가능하다.

파이프는 매우 무겁기 떄문에, 유현이는 파이프를 밀어서 이동시키려고 한다. 벽에는 새로운 벽지를 발랐기 때문에, 파이프가 벽을 긁으면 안 된다. 즉, 파이프는 항상 빈칸만 차지해야 한다.

파이프를 밀 수 있는 방향은 총 3가지가 있으며, →, ↘, ↓ 방향이다. 파이프는 밀면서 회전시킬 수 있다. 회전은 45도만 회전시킬 수 있으며, 미는 방향은 오른쪽, 아래, 또는 오른쪽 아래 대각선 방향이어야 한다.

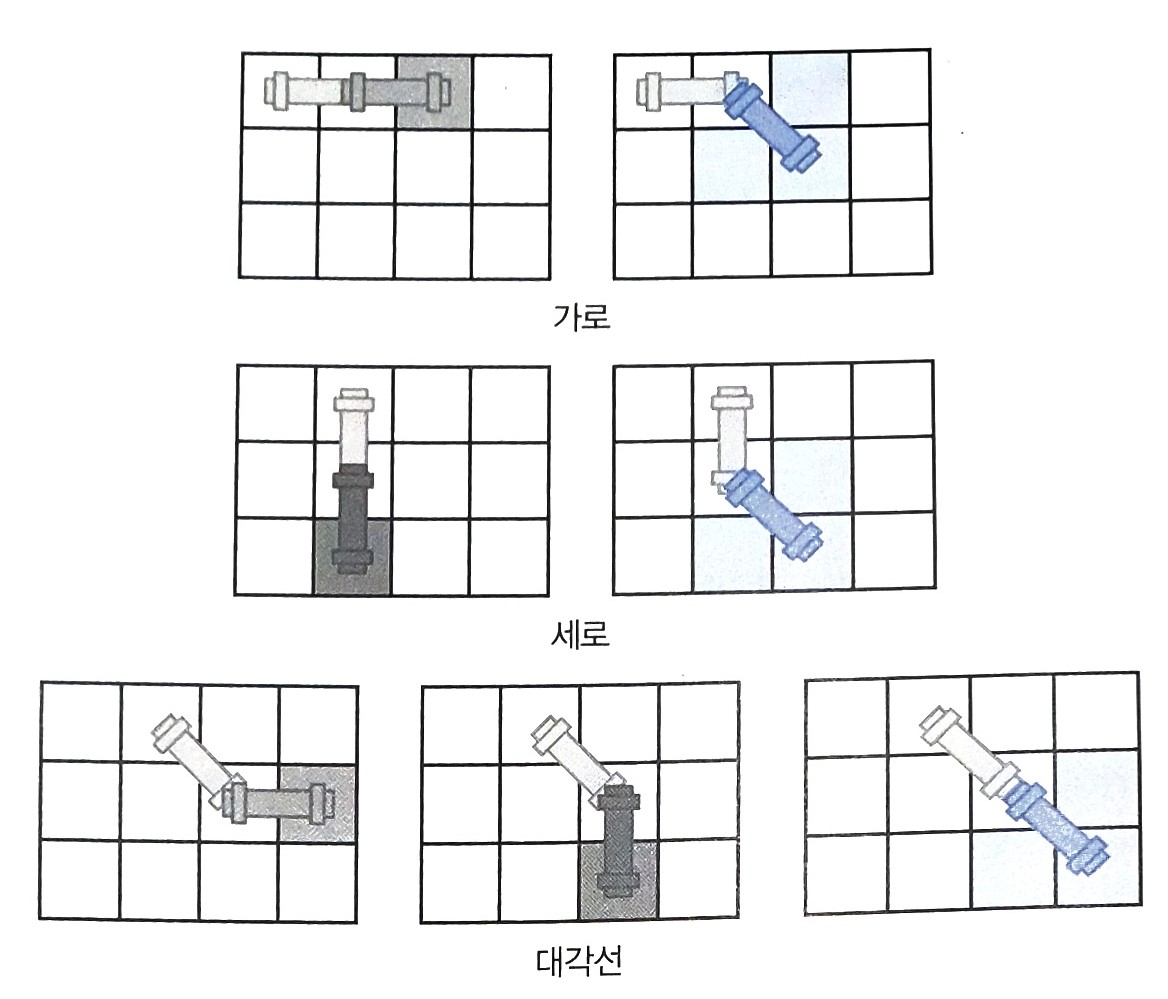
파이프가 가로로 놓여진 경우에 가능한 이동 방법은 총 2가지, 세로로 놓여진 경우에는 2가지, 대각성 방향으로 놓여진 경우에는 3가지가 있다.

아래 그림은 파이프가 놓여진 방향에 따라서 이동할 수 있는 방법을 모두 나타낸 것이고, 꼭 빈칸이어야 하는 곳은 색으로 표시되어져 있다.

가장 처음에 파이프는 (1, 1)와 (1, 2)를 차지하고 있고, 방향은 가로이다. 파이프의 한쪽 끝을 (N, N)로 이동시키는 방법의 개수를 구해보자.


[입력]
첫째 줄에 집의 크기 $N(3 \le N \le 16)$이 주어진다. 둘쨰 줄부터 N개의 줄에는 집의 상태가 주어진다. 빈칸은 0, 벽은 1로 주어진다. (1, 1)과 (1, 2)는 항상 빈칸이다.


[출력]
첫째 줄에 파이프의 한쪽 끝을 (N, N)으로 이동시키는 방법의 수를 출력한다. 이동시킬 수 없는 경우에는 0을 출력한다. 방법의 수는 항상 1,000,000보다 작거나 같다.

예제 입력 1	예제 출력 1
3	1
0 0 0
0 0 0
0 0 0

예제 입력 2	예제 출력 2
4	3
0 0 0 0
0 0 0 0
0 0 0 0
0 0 0 0

예제 입력 3	예제 출력 3
5	0
0 0 1 0 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0

예제 입력 4	예제 출력 4
6	13
0 0 0 0 0 0
0 1 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0

문제설명

가로와 세로의 길이가 n이고 0과 1로 이루어진 집의 상태가 입력으로 주어진다.
집의 상태가 0이면 파이프를 둘 수 있고, 1이면 파이프를 둘 수 없다.

파이프는 아래와 같이 집의 칸 2개를 사용하여 둘 수 있고,

3가지 방향이 가능하다.
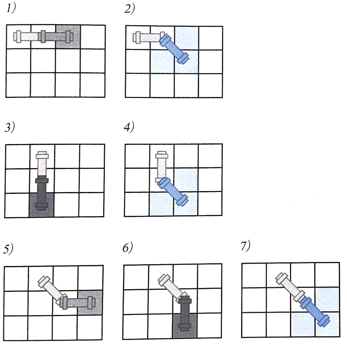
이때 파이프는

7가지의 이동 방법이 있다.
(1, 1)(1, 2)위치에 있는 파이프의 한 쪽 끝을 (n, n) 좌표로 이동시키는 방법의 개수를 구하는 문제이다.

• 우선 파이프의 모형은 3가지가 가능하다.

1. 파이프가 가로 형태라면 0으로,
2. 파이프가 세로 형태라면 1로,
3. 파이프가 대각선 형태라면 2로 설정해보자.

• 가로 형태에서 이동 가능한 방법은

1. 가로에서 가로 0 → 0
2. 가로에서 대각선 0 → 2

• 세로 형태에서 이동 가능한 방법은

3. 세로에서 세로 1 → 1
4. 세로에서 대각선 1 → 2

• 대각선 형태에서 이동 가능한 방법은

5. 대각선에서 가로 2 → 0
6. 대각선에서 세로 2 → 1
7. 대각선에서 대각선 2 → 2

• 7가지가 있고 , 이 7가지를 재귀함수를 통해 모든 경우의 수를 전부 구해주면 된다.
  
  

해답코드

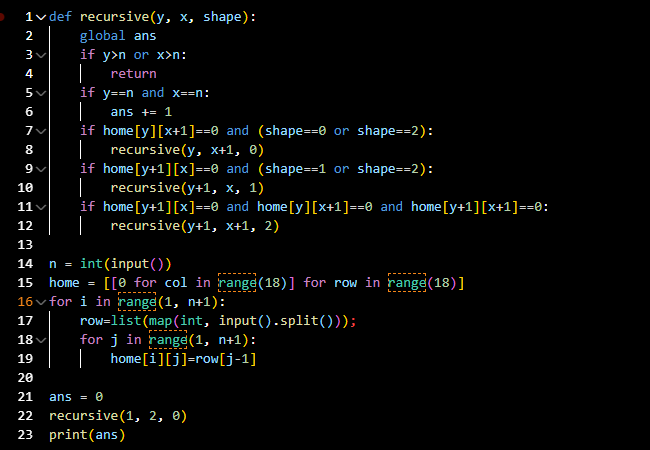
크게 3가지의 의미로 나눌 수 있다.

1. 코드라인 1~12: 문제를 해결하기 위한 재귀함수이다.
2. 코드라인 14~19: n과 집의 상태를 입력받는다. 위 코드의 경우 인덱스를 좀 더 직관적으로 관리하기 위해 배열의 인덱스를 0이 아닌 1부터 시작하게 해두었다(파이프의 위치 (1, 1)(1, 2)를 좀 더 직관적으로 이용할 수 있다).
3. 코드라인 21~33: 재귀함수를 실행하고 정답을 출력한다.

코드라인 1~12를 자세히 살펴보자.

• 코드라인 1: 파이프의 한쪽 끝 위치(y, x)와 현재 파이프의 모양(가로, 세로 혹은 대각선)의 정보를 담고 있는 shape 변수를 함수의 인자로 받는다.
• 코드라인 2: 문제의 정답을 저장하기 위한 변수 ans이다.
• 코드라인 3~4: 파이프의 위치(y, x)가 n보다 크다면 집의 범위를 넘었으므로 반환한다.
• 코드라인 5~6: 파이프의 위치(y, x)가 (n. n)이라면 ans+=1로 정답을 1 증가시킨다.
• 코드라인 7~8: 파이프의 위치(y, x+1)이 (오른쪽) 1이 아니고 (1은 파이프를 돌 수 없는 위치) 현재 모양이 가로 혹은 대각선이라면 재귀함수(y, x+1, 가로)를 실행한다.
• 코드라인 9~10: 파이프의 위치(y+1, x)가 (아래쪽) 1이 아니고 현재 모양이 세로 혹은 대각선이라면 재귀함수(y+1, x, 세로)를 실행한다.
• 코드라인 11~12: 파이프의 위치(y+1, x+1)이(대각선-오른쪽아래) 1이 아니면 재귀함수(y+1, x+1, 대각선)를 실행한다.

---

분할정복

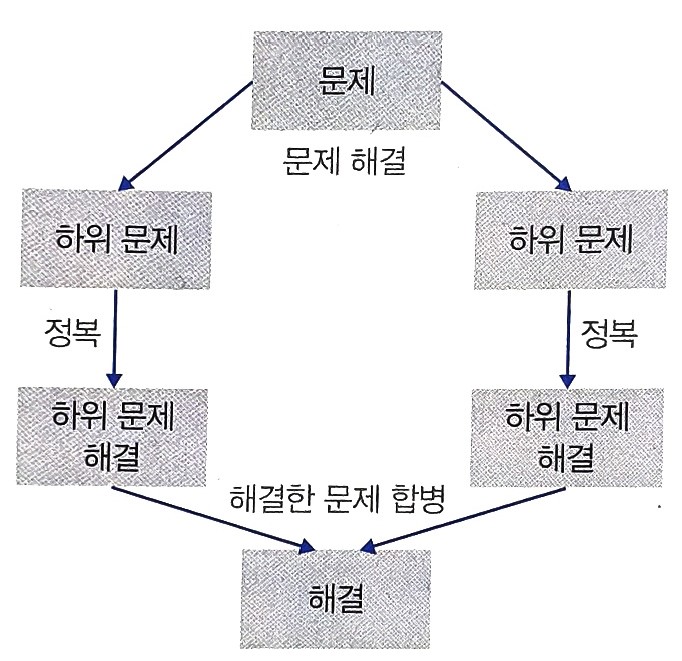
• 분할정복은 주어진 문제를 작은 사례로 나누고(Divide) 각각의 작은 문제들을 해결하여 정복(Conquer) 해나가는 방법이다.
• 보통 분할정복은 3가지 단계를 거친다.
  • 분할 단계 : 해결하고자 하는 문제를 작은 크기의 동일한 문제들로 분할(divide)한다.
  • 정복 단계 : 각각의 작은 문제를 동일한 방법으로 재귀적(recursive)으로 해결한다.
  • 합병 단계 : 작은 문제의 해를 합하여(merge) 원래 문제에 대한 해를 구한다.
    
    
    

분할정복을 이용한 예제 1 - 색종이 만들기

[문제]
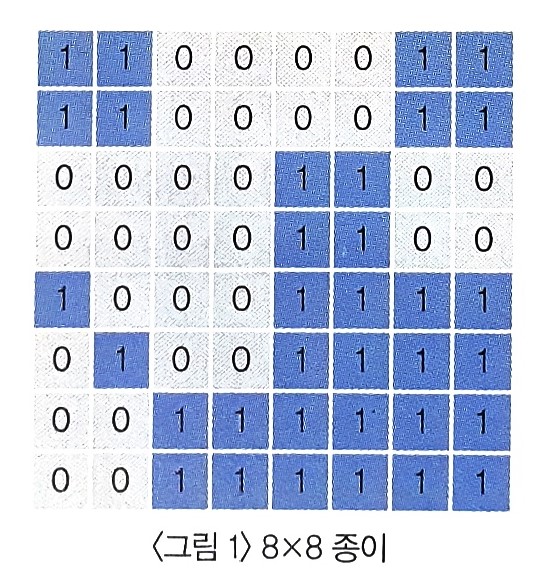
아래 <그림 1>과 같이 여러개의 정사각형칸들로 이루어진 정사각형 모양의 종이가 주어져 있고, 각 정사각형들은 하얀색으로 칠해져 있거나 파란색으로 칠해져 있다. 주어진 종이를 일정한 규칙에 따라 잘라서 다양한 크기를 가진 정사각형 모양의 하얀색 또는 파란색 색종이를 만들려고 한다.

전체 종이의 크기가 N X N($N=2^k$, $k$는 1이상 7 이하의 자연수)이라면 종이를 자르는 규칙은 다음과 같다.

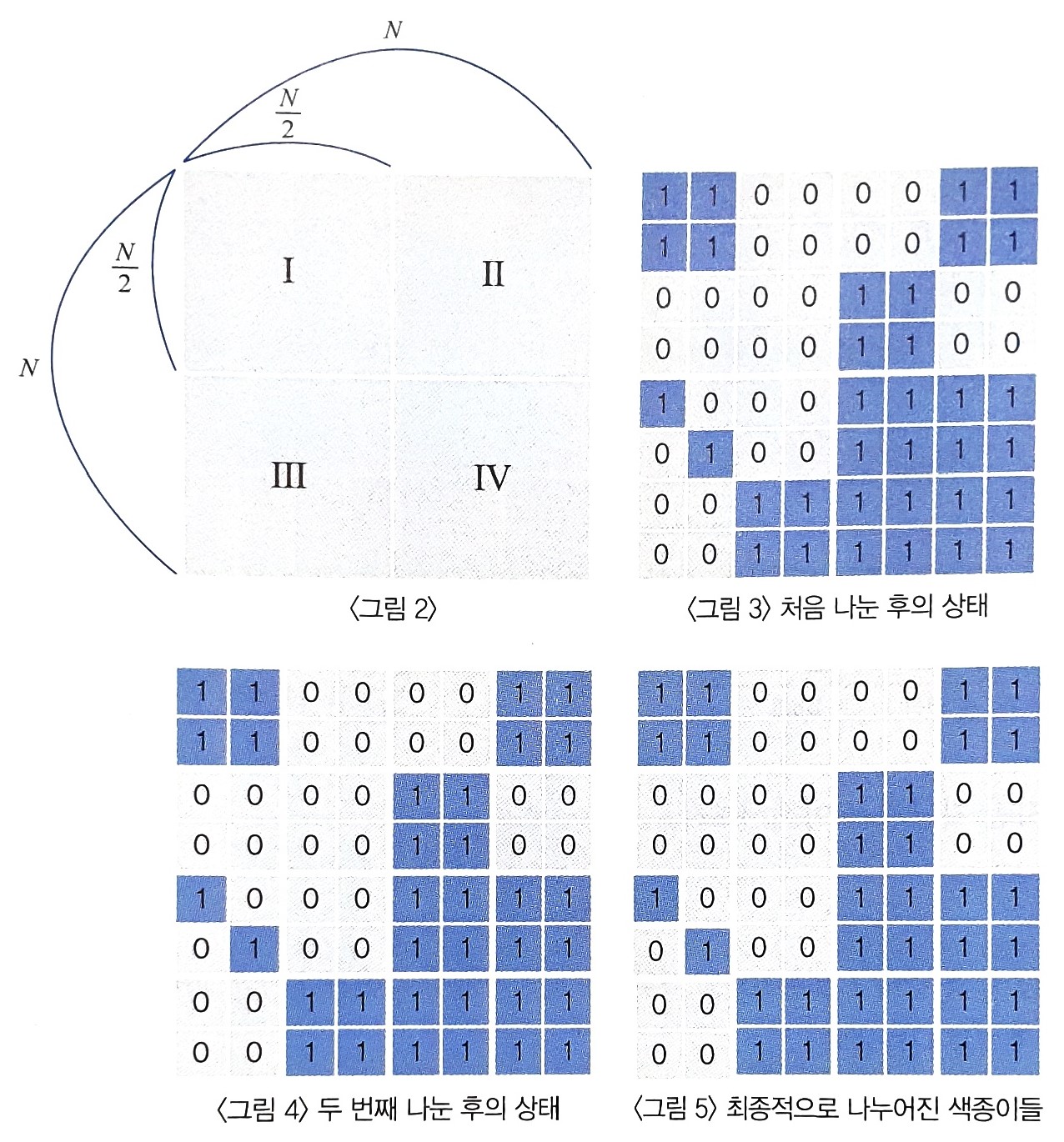
전체 종이가 모두 같은 색으로 칠해져 있지 않으면 가로와 세로로 중간 부분을 잘라서 <그림 2>의 Ⅰ, Ⅱ, Ⅲ, Ⅳ와 같이 똑같은 크기의 네 개의 N / 2 X N / 2 색종이로 나눈다. 나누어진 종이 Ⅰ, Ⅱ, Ⅲ, Ⅳ 각각에 대해서도 앞에서와 마찬가지로 모두 같은 색으로 칠해져 있지 않으면 같은 방법으로 똑같은 크기의 네 개의 색종이로 나눈다. 이와 같은 과정을 잘라진 종이가 모두 하얀색 또는 모두 파란색으로 칠해져 있거나, 하나의 정사각형 칸이 되어 더 이상 자를 수 없을 때까지 반복한다.

위와 같은 규칙에 따라 잘랐을 때 <그림 3>은 <그림 1>의 종이를 처음 나눈 후의 상태를, <그림 4>는 두 번째 나눈 후의 상태를, <그림 5>는 최종적으로 만들어진 다양한 크기의 9장의 하얀색 색종이와 7장의 파란색 색종이를 보여주고 있다.

입력으로 주어진 종이의 한 변의 길이 N과 각 정사각형칸의 색(하얀색 또는 파란색)이 주어질 때 잘라진 하얀색 색종이와 파란색 색종이의 개수를 구하는 프로그램을 작성하시오.


[입력]
첫째 줄에는 전체 종이의 한 변의 길이 N이 주어져 있다. N은 2, 4, 8, 16, 32, 64, 128 중 하나이다. 색종이의 각 가로줄의 정사각형칸들의 색이 윗줄부터 차례로 둘째 줄부터 마지막 줄까지 주어진다. 하얀색으로 칠해진 칸은 0, 파란색으로 칠해진 칸은 1로 주어지며, 각 숫자 사이에는 빈칸이 하나씩 있다.


[출력]
첫째 줄에는 잘라진 하얀색 색종이의 개수를 출력하고, 둘째 줄에는 파란색 색종이의 개수를 출력한다.

예제 입력 1	예제 출력 1
8	9
1 1 0 0 0 0 1 1	7
1 1 0 0 0 0 1 1
0 0 0 0 1 1 0 0
0 0 0 0 1 1 0 0
1 0 0 0 1 1 1 1
0 1 0 0 1 1 1 1
0 0 1 1 1 1 1 1
0 0 1 1 1 1 1 1

문제설명

문제의 <그림 1>과 같이 1 또는 0으로 이루어진 정사각형이 주어진다. 1은 파란색 종이를 나타내고, 0은 하얀색 종이를 나타낸다.

종이의 길이가 $n$이고 각 종이의 좌표를 (x, y)로 표시한다면

처음으로는
(0~n, 0~n) 구역이 모두 같은 색(모두 하얀색 또는 모두 파란색)인지 확인하여 모두 같은 색이라면 해당 색깔의 종이 수를 1 더하고 프로그램을 종료한다.
모두 같은 색이 아니라면

(0~n/2, 0~n/2)
(n/2~n, 0~n/2)
(0~n/2, n/2~n)
(n/2~n, n/2~n)

4구역으로 나눈 후 각 구역마다 모두 같은 색(모두 하얀색 또는 모두 파란색)이라면 그 색깔의 종이수를 1 더하고, 같은 색이 아니라면 해당 구역을 다시 한 번

(0~n/2, 0~n/2)
(n/2~n, 0~n/2)
(0~n/2, n/2~n)
(n/2~n. n/2~n)

4구역으로 나눈다.

이런 식으로 계속 반복하여 총 하얀색 종이의 개수와 총 파란색 종이의 개수를 출력하면 되는 문제이다.

이 예제는 정말 분할정복의 정석적인 예제라고 할 수 있다.

1. 분할 단계
   하얀색과 파란색 종이의 수를 구하기 위해
   (0~n/2, 0~n/2)
   (n/2~n, 0~n/2)
   (0~n/2, n/2~n)
   (n/2~n, n/2~n)
   구역을 4구역으로 나누어 준다.
   
   
2. 정복 단계
   해당 구역의 종이가 모두 같은 색이면 합병 단계로 넘어가고,
   해당 구역의 종이가 모두 같은 색이 아니라면 다시 분할 단계로 넘어간다.
   
   
3. 합병
   해당 색깔의 종이의 수를 1씩 더해준다.
   
   

해답코드

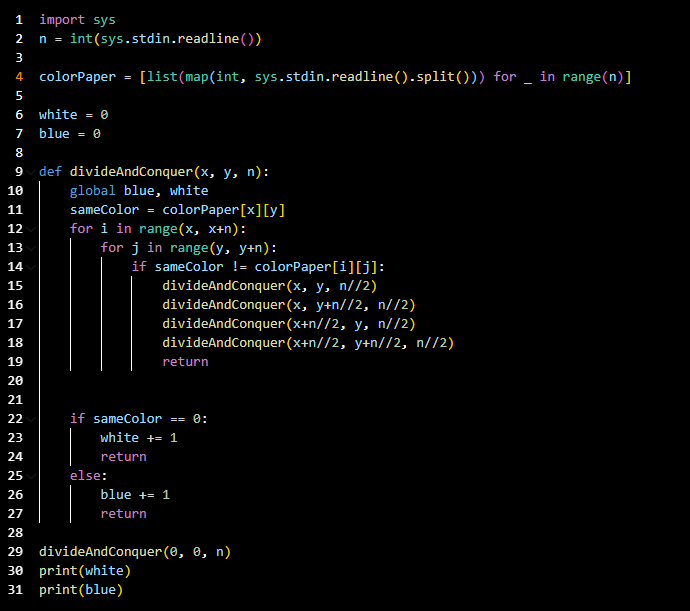
• 코드라인 4: 0과 1로 이루어진 종이의 상태를 입력받는다.
• 코드라인 9~27: 분할정복을 위한 함수를 생성한다.
  • 코드라인 9: 함수의 입력으로는 현재 좌표 x, y와 해당구역의 크기 n을 받는다.
  • 코드라인 10: 파란색 종이와 하얀색 종이의 수를 저장하기 위한 변수를 생성한다.
  • 코드라인 11: 해당 구역이 모두 같은 색인지 확인하기 위한 기준 변수를 생성한다.
  • 코드라인 14: 코드라인 11에서 생성한 기준색과 다른 색이 있다면
  • 코드라인 15: (x, y, n//2) → (x~x+n/2, y~y+n/2) 구역을 분할정복한다.
  • 코드라인 16: (x, y+n//2, n//2) → (x~x+n/2, y+n/2~y+n) 구역을 분할정복한다.
  • 코드라인 17: (x+n//2, y, n//2) → (x+n/2~x+n, y~y+n/2) 구역을 분할정복한다.
  • 코드라인 18: (x+n//2, y+n//2, n//2) → (x+n/2~x+n, y+n/2~y+n) 구역을 분할정복한다.
  • 코드라인 10: 함수를 종료한다.
• 코드라인 19에서 종료가 되지 않았다면 해당 구역은 모두 같은 색인데,
  • 코드라인 22~24: 색이 흰색이라면 하얀색 종이 수를 1 증가시킨다.
  • 코드라인 25~27: 색이 파란색이라면 파란색 종이 수를 1 증가시킨다.
  • 코드라인 29: 분할정복 함수를 실행한다.
  • 코드라인 30: 하얀색 종이 수를 출력한다.
  • 코드라인 31: 파란색 종이 수를 출력한다.