
탐욕법
- 탐욕법(greedy)이란 문제를 해결할 때, 매 순간 눈앞에 보이는 최선의 선택지를 고르는 방법이다.
- 매순간 최적의 답을 위해서 어느 정도 타협이 필요한 알고리즘이다.
- 긜고 타협선을 어디다 두는지는 프로그래머가 결정해야 할 몫이다.
- 우선순위 큐와는 다르게 우선순위가 높은 데이터를 통한 문제 풀이가 아닌 그때그때 상황에 맞는 데이터를 통해 작업할 때 자주 쓰인다.
탐욕법을 이용한 예제 1 - 잃어버린 괄호
[문제]
세준이는 양수와 +, -, 그리고 괄호를 가지고 식을 만들었다. 그리고 나서 세준이는 괄호를 모두 지웠다. 그리고 나서 세준이는 괄호를 적절히 쳐서 이 식의 값을 최소로 만들려고 한다.괄호를 적절히 쳐서 이 식의 값을 최소로 만드는 프로그램을 작성하시오.
[입력]
첫째 줄에 식이 주어진다. 식은 '0' ~ '9', '+', 그리고 '-'만으로 이루어져 있고, 가장 처음과 마지막 문자는 숫자이다. 그리고 연속해서 두 개 이상의 연산자가 나타나지 않고, 5자리보다 많이 연속되는 숫자는 없다. 수는 0으로 시작할 수 있다. 입력으로 주어지는 식의 길이는 50보다 작거나 같다.
[출력]
첫쨰 줄에 정답을 출력한다.
예제 입력 1 예제 출력 1
예제 입력 2 예제 출력 2
예제 입력 3 예제 출력 3
문제설명
식이 주어졌을 떄 괄호를 적절히 쳐서 나올 수 있는 결괏값의 최솟값을 찾아야 하는 문제이다. 이 문제에서는 괄호를 언제 추가해야 하는지가 관건이다.
- 이러한 수학적 사고력을 요구한다 싶은 문제를 볼 때, 아래와 같은 고려사항을 먼저 확인한다.
1) 완전 탐색을 했을 때 시간초과가 나지 않는지 시간복잡도를 계산한다.
2) 문제 규칙을 찾는다.
3) 탐욕법을 생각한다.- 1)의 완전 탐색을 이용하면 괄호를 쳐주어야 하는 상황이 32개만 넘어도 시간복잡도는 으로 20초 이상의 시간이 걸린다.
- 2)의 문제 규칙을 찾아보자.
55-50+40의 경우
50-(50+40) = -35로 최솟값이 된다.
10+55-50+40의 경우
10+55-(50+40) = -25로 최솟값이 된다.
10+55-50+40-10의 경우
10+55-(50+40)-10 = -35로 최솟값이 된다.
10+55-50+40-10+5의 경우
10+55-(50+40)-(10+5) = -30으로 최솟값이 된다.
10+55-50+40-10+5+5의 경우
10+55-(50+40)-(10+5+5) = -25로 최솟값이 된다.- 문제의 테스트 케이스를 만들어보며 어떤 상황에서 최소한의 값이 나오는지 확인해보면 ,규칙을 찾을 수 있다.
- 규칙은 아래와 같다.
1) 첫 숫자부터 마이너스(-)가 나오기 이전까지의 수는 전부 더해주면 된다.
2) 그 뒤에 마이너스(-)가 나온 이후의 숫자는 괄호를 치면 전부 뺼 수 있으므로 전부 뺴주면 된다."문제의 규칙을 찾아보니 현재에서 최선을 선택하기 위해서는 처음 마이너스(-)가 나오기 전의 수들은 모두 더해주고 그 후부터 모든 수는 뺴주면 되겠네?"
- 이는 앞서 설명한 탐욕법을 이용하여 풀어주는 방식이다.
해답코드
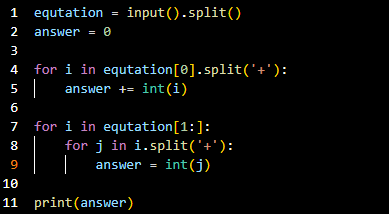
- 코드라인 1~5: 마이너스(-)가 나오기 이전의 수는 answer에 모든 수를 더한다.
- 코드라인 7~9: 마이너스(-)가 나온 이후의 수는 answer에 모든 수를 뺀다.
- 코드라인 11: 정답인 answer를 출력한다.
탐욕법을 이용한 예제 2 - 회의실 배정
[문제]
한 개의 회의실이 있는데 이를 사용하고자 하는 N개의 회의에 대하여 회의실 사용표를 만들려고 한다. 각 회의 I에 대해 시작시간과 끝나는 시간이 주어져 있고, 각 회의가 겹치지 않게 하면서 회의실을 사용할 수 있는 회의의 최대 개수를 찾아보자. 단, 회의는 한번 시작하면 중간에 중단될 수 없으며 한 회의가 끝나는 것과 동시에 다음 회의가 시작될 수 있다. 회의의 시작시간과 끝나는 시간이 같을 수도 있다. 이 경우에는 시작하자마나 끝나는 것으로 생각하면 된다.
[입력]
첫쨰 줄에 회의의 수 이 주어진다. 둘째 줄부터 N+1줄까지 각 회의의 정보가 주어지는데 이것은 공백을 사이에 두고 회의의 시작시간가ㅗ 끝나는 시간이 주어진다. 시작시간과 끝나는 시간은 보다 작거나 같은 자연수 또는 0이다.
[출력]
첫째 줄에 사용할 수 있는 회의의 최대 개수를 출력한다.
예제 입력 1 예제 출력 1 11 4 1 4 3 5 0 6 5 7 3 8 5 9 6 10 8 11 8 12 2 13 12 14
문제설명
이 문제는 한 개의 회의실이 있고 이를 이용하고자 하는 n개의 회의가 있다. 각 회의에 대한 시작 시간과 끝나는 시간이 주어질 때 각 회의가 겹치지 않게 회의실을 사용할 수 있는 최대 회의 수를 구하면 되는 것이다.
- 우선 바로 떠오르는 방법으로는
1. (회의가 끝나는 시간 - 회의가 시작되는 시간)이 작은 것부터 고른다.
2. 회의가 시작되는 시간이 작은 값부터 고른다.
3. 회의가 끝나는 시간이 작은 값부터 고른다.- 전부 무언가 부족하다.
- 회의 수가 최대가 되려면 많은 수의 회의가 이루어 질 수 있게 회의를 골라야 한다.
1. 회의가 끝나는 시간이 빠를수록 더 많은 회의를 고를 수 있다.
2. 끝난 시간 이후부터 가장 빨리 시작되는 회의를 골라야 한다.- 이 2가지를 파악하는 것이 문제의 핵심인데 이를 구현하기 위해서는 끝나는 시간이 작을수록 앞으로 오게 정렬하되, 끝나는 시간이 같다면 시작 시간이 작은 회의를 앞으로 오게 정렬해야 한다.
- 알고리즘 문제를 푸는 데 있어서 매우 많이 사용되는 정렬 방법을 하나 배워보자.
- 리스트의 정렬 기준을 프로그래머에게 할당하는 방법으로 아래와 같은 기법이 있다.
변수명.sort(key=lambda x: (x[1], x[0]))- 위 코드는 x[1](회의가 끝나는 시간)의 작은 값이 앞에 오게 오름차순으로 정렬하되, 회의가 끝나는 시간이 같다면 x[0](회의가 시작되는 시간)의 작은 값이 앞에 오게 오름차순으로 정렬한다.
- 다시 정리하자면,
- 최대 회의 수를 구하기 위해 회의가 끝나는 시간이 짧은 것을 택한다.
- 끝나는 시간부터 매 순간마다 회의가 시작되는 시간이 빠른 것을 다시 고르며 이를 반복한다.
해답코드
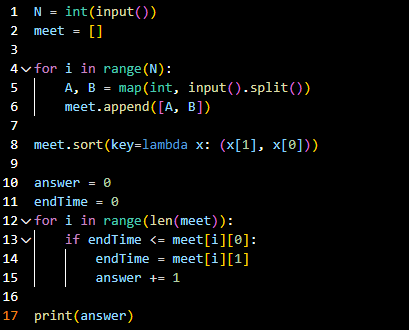
- 코드라인 1~6: n과 회의실 상태를 입력받는다.
- 코드라인 8: 회의가 끝나는 시간이 빠른 순으로. 끝나는 시간이 같다면 회의 시작 시간이 빠른 순으로 리스트를 정렬한다.
- 코드라인 10, 11: 정답과 끝나는 시간을 저장하기 위한 변수를 생성한다.
- 코드라인 13~15: 회의가 끝난 시간보다 시작 시간이 크다면 answer += 1, 회의가 끝난 시간을 시작 시간에 해당하는 회의가 끝난 시간 값으로 바꾸어준다.
- 코드라인 17: 정답을 출력한다.
탐욕법을 이용한 예제 3 - 소트
[문제]
크기가 N인 배열 A가 있다. 배열에 있는 모든 수는 서로 다르다. 이 배열을 소트할 때, 연속된 두 개의 원소만 교환할 수 있다. 그리고, 교환은 많아봐야 S번 할 수 있다. 이때, 소트한 결과가 사전순으로 가장 뒷서는 것을 출력한다.
[입력]
첫째 줄에 N이 주어진다. N은 50보다 작거나 같은 자연수이다. 둘째 줄에는 각 원소가 차례대로 주어진다. 이 값은 1000000보다 작거나 같은 자연수이다. 마지막 줄에는 S가 주어진다. S는 1000000보다 작거나 같은 음이 아닌 정수이다.
[출력]
첫째 줄에 문제의 정답을 출력한다.
예제 입력 1 예제 출력 1 7 20 10 30 40 50 60 70 10 20 30 40 50 60 70 1
예제 입력 2 예제 출력 2 5 5 3 2 1 4 3 5 1 2 4 2
예제 입력 3 예제 출력 3 10 20 19 18 17 16 15 14 13 12 11 19 20 17 18 15 16 13 14 11 12 5
문제설명
n개의 크기를 가진 배열 a가 주어지며, 이 배열은 연속된 2개의 원소만 교환할 수 있다 (a[i]와 a[i+1] 혹은 a[i-1]와 a[i]). 최대 s번 교환하여 만들 수 있는 배열 중에서 사전 순으로 가장 뒷서는 것을 출력해야 하는 문제이다.
- n = 5이고 배열 arr = 3 5 1 2 4 이라면 s의 값에 따라 정답은 아래와 같다.
| s | arr |
|---|---|
| 1 | 5 3 1 2 4 |
| 2 | 5 3 2 1 4 |
| 3 | 5 3 4 1 2 |
| 4 | 5 4 3 1 2 |
| 5 | 5 4 3 2 1 |
s가 1일 때 3과 5의 위치를 바꿨다.
s가 2일 때 3과 5의 위치를 바꾸고 -> 5 3 1 2 4
1과 2의 위치를 바꿨다 -> 5 3 2 1 4
s가 3일 때 3과 5의 위치를 바꾸고 -> 5 3 1 2 4
4와 2의 위치를 바꾸고 -> 5 3 1 4 2
1과 4의 위치를 바꿨다 -> 5 3 4 1 2- 문제에서 연속된 수만 교체 할 수 있다고 했는데, 이는 결국 인덱스 차이가 남은 이하라면 신경쓰지 않아도 되는 것을 알 수 있다.
즉 s가 3일 때 3과 5의 위치를 바꾸고 -> 5 3 1 2 4, s=2
1과 4의 위치를 바꿨다 -> 5 3 4 1 2, s=0- 사전 순으로 뒤에 서기 위해서는 왼쪽에서 오른쪽으로 갈수록 수가 작아져야 한다.
- 그러므로 왼쪽에서 오른쪽으로 순회한 인덱스를 기준으로 오른쪽에 있는 수 중 남은 번을 교체해서 가져올 수 있는 최댓값을 매순간 바꿔주는 것이 정답이다.
for i in range(N):
idx = i
for j in range(N-1, i, -1):
if arr[idx] < arr[j] and j-i <= s:
idx = j- 이 코드는 idx 변수에 i의 기준으로 오른쪽에 있는 수 중 번의 교환
(j-i<=s)으로 바꿀 수 있는 최댓값의 위치를 찾는다. - 결국 핵심은 왼쪽에 있는 수일수록 값을 크게 만드는 것이다.
해답코드
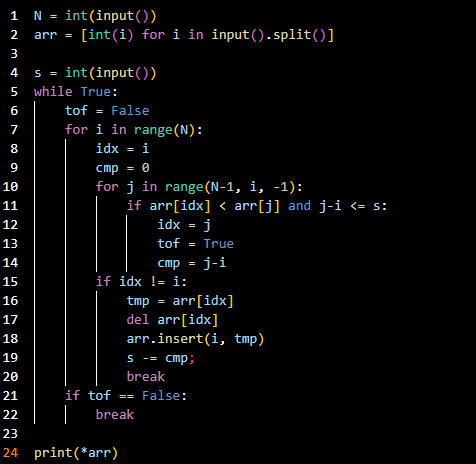
- 코드라인 5: 반복문을 계속 돌린다(맨 왼쪽에 있는 수를 매순간 순간 크게 만들기 위해).
- 코드라인 6: 종료 지점을 나타내기 위한 변수를 생성한다.
- 코드라인 7~14: 위에서 설명했듯이 idx 변수에 i의 위치를 기준으로 오른쪽에 있는 수 중 남은 s번 교체해서 바꿀 수 있는 최댓값의 위치를 저장한다.
idx 변수와 i와 다르다면 바꿀 수를 찾은 것이고tof=True로 해두어 이후에 while문을 종료되게 하지 않는다. cmp 변수는 교체 횟수를 임시로 저장하기 위한 변수이다. - 코드라인 15~20: 배열의 idx 위치값과 i 위치값을 바꿔준다. 그 후 s는 cmp값만큼 빼준다. 그리고 for문을 탈출한다(for문을 탈출하는 이유는 수를 바꿔준 뒤 다시 왼쪽부터 수를 순회하기 위해서이다. 이는 매순간 맨 왼쪽부터 큰 수가 오게 하기 위해서이다).
- 코드라인 21~22:
tof=False이라면 바꿀 수를 찾지 못한 것이므로 while문을 탈출한다. - 코드라인 24: 정답을 출력한다.
탐욕법을 이용한 예제 4 - 소트
[문제]
N개의 정수가 주어지면, 이것을 두 수가 연속된 값이 아니게 정렬하는 프로그램을 작성하시오. 가능한 것이 여러 가지라면 사전순으로 가장 앞서는 것을 출력한다.
[입력]
첫째 줄에 N이 주어진다. N은 50보다 작거나 같은 자연수이다. 둘째 줄에는 N개의 수가 주어진다. N개의 수는 1,000보다 작거나 같은 자연수 또는 0이다.
[출력]
첫째 줄에 문제의 정답을 출력한다.
예제 입력 1 예제 출력 1 3 1 3 2 1 2 3
예제 입력 2 예제 출력 2 9 2 2 2 2 2 1 1 1 1 1 1 1 1 2 2 2 2 2
예제 입력 3 예제 출력 3 2 1 2 2 1
예제 입력 4 예제 출력 4 6 1 3 2 4 6 5 1 2 3 4 5 6
예제 입력 5 예제 출력 5 6 1 1 3 3 2 2 1 1 2 2 3 3
문제설명
n개의 정수가 주어질 때, 두 수가 연속된 값이 아니게 정렬
(a[i]+1 != a[i+1])하는 프로그램을 만들어야 하는 것이다. 이때 가능한 것이 여러 개라면 사전 순으로 가장 앞서는 것을 출력해야 한다.
- 우선 사전 순으로 가장 앞선다는 것은 배열의 왼쪽일수록 수가 작아야 한다(오름차순).
- 문제는
a[i]+1의 값은a[i+1]과 다르게 배열을 재정렬하는 것인데, 다양한 테스트 케이스를 만들어 문제의 조건부터 찾아야 한다.
1)
1-1)
n=5 이고 1 1 2 2 4 라면
a[0]+2 이상의 값이 배열 안에 존재하기 때문에 1을 전부 출력할 수 있다.
그 후 4를 출력하고, 2를 전부 출력해주면 된다.
1-2)
n=4이고 1 1 2 2 라면
1을 먼저 출력할 수 있는 방법이 없다.
따라서 2를 먼저 출력하고 또 2를 출력하고, 1을 출력할 수 있다.
2)
2-1)
n=6이고 1 1 1 1 3 3 이라면
a[0]=1의 +1 값인 2가 없으므로 1을 전부 출력할 수 있다.
그 후 3 또한 모두 출력해주면 된다.- 문제의 규칙을 살펴보면
- 사전 순으로 가장 앞선 것을 출력해주기 위해 우선 배열이 오름차순으로 정렬되어야 한다.
a[i]값에 대하여
1) a[i]+1의 값이 배열 안에 존재할 때
1-1) a[i]+2 이상의 값 k가 배열 안에 존재한다면
배열 안에 있는 a[i]값을 전부 출력하고, k를 출력한다.
1-2) a[i]+2의 값이 배열 안에 존재하지 않는다면
배열 안에 있는 a[i]+1의 값을 한번 출력한다.
2) a[i]+1의 값이 배열 안에 존재하지 않는다면
배열 안에 있는 a[i] 값을 전부 출력할 수 있다.해답코드
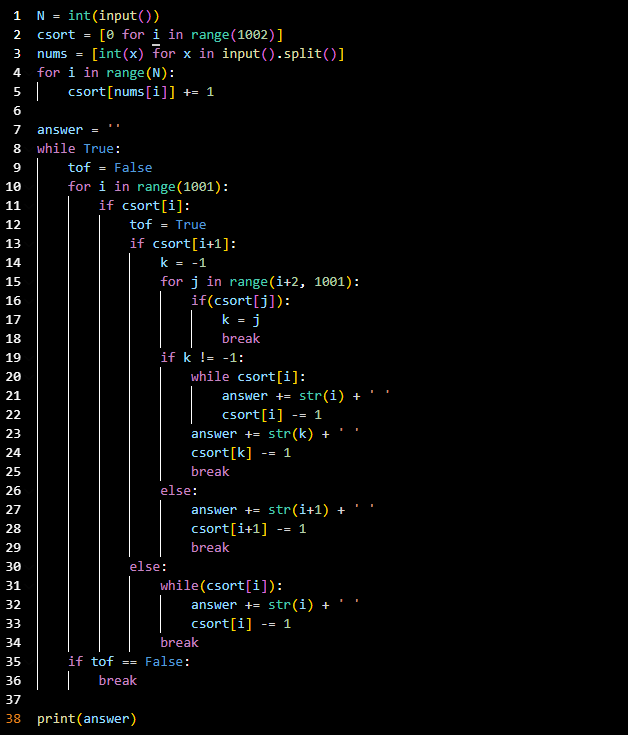
- 코드라인 1~5: n개의 정수를 변수 csort에 계수정렬해 준다.
- 코드라인 8: 종료 시점까지 while문을 계속 돌린다.
- 코드라인 10: 0~1000까지 for문을 탐색한다.
- 코드라인 11: 해당 계수
i에 해당하는cosrt[i]가 존재할 때- 코드라인 13: 계수
i+1에 해당하는cosrt[i+1]이 존재한다면 - 코드라인 14~18: 계수
i+2이상의k값이csort[k]에 존재하는지 확인하고- 코드라인 19:
csort[k]가 존재한다면 - 코드라인 20~25:
csort[i]값을 전부 출력하고,csort[k]를 한번 출력한다. - 코드라인 26:
csort[k]가 존재하지 않는다면 - 코드라인 27~29:
csort[i+1]의 값을 한번 출력한다.
- 코드라인 19:
- 코드라인 30: 계수
i+1에 해당하는csort[i+1]이 존재하지 않는다면 - 코드라인 31~34:
csort[i]를 전부 출력한다.
- 코드라인 13: 계수
- 코드라인 35:
tof값이False라면(더 이상 배열에 수가 남아 있지 않다면)while문을 종료한다. - 코드라인 38: 정답을 출력한다.
탐욕법을 이용한 예제 5 - 대결
[문제]
팀 A와 B가 대결을 하려고 한다. 각 팀에 속한 사람은 다른 팀에 속한 사람과 대결을 해야 한다. 두 팀에 속한 각 사람은 대결을 한 번씩 해야 한다. 대결의 승자는 2점을 획득하고, 무승부인 경우에는 1점을 획득한다.팀 A에 속한 사람의 능력치는 이고, 팀 B에 속한 사람의 능력치는 이다. 대결은 능력치가 높은 사람이 이기며, 능력치가 같은 경우 비긴다.
두 팀의 능력치가 주어졌을 때, 팀 A가 얻을 수 있는 점수의 최댓값을 구해보자.
[입력]
첫째 줄에 팀에 속한 사람의 수 N이 주어진다. 둘째 줄에는 이 주어지고, 셋째 줄에는 이 주어진다.
[출력]
첫째 줄에 팀 A가 얻을 수 있는 점수의 최댓값을 출력한다.
[제한]
예제 입력 1 예제 출력 1 2 4 5 8 7 3
예제 입력 2 예제 출력 2 2 2 7 3 5 8
예제 입력 3 예제 출력 3 3 4 10 5 1 10 5 1
예제 입력 4 예제 출력 4 4 5 1 10 7 4 15 3 8 7
문제설명
팀 A와 B가 있을 때, 각 팀에는 N명의 사람이 있으며 각각 한 번의 대결을 다른 팀과 한다. 이때 대결의 승자는 2점을 획득하고, 무승부인 경우 1점을 획득한다. 팀 A가 얻을 수 있는 최대 점수를 구하는 것이다.
- 문제를 해결함에 있어 기본적으로 A가 최대 점수를 얻기 위해서는 B팀과의 대결에서 최대한 많은 승리를 해야 한다. 그러기 위해서 생각할 수 있는 방법으로는
"A팀에서 가장 낮은 값 k보다 작은 수 중에서 가장 큰 값을 B팀에서 찾아야 한다." - 문제의 핵심은 위의 한 줄이다.
- 그렇게 A가 최적의 방법으로 많은 승리를 얻은 후 무승부가 가능한 경우를 구해주면 된다.
- 예제 입력 4를 조금 수정해서 아래와 같은 A, B팀이 있을 때,
A 1 10 7 4
B 15 7 3 7- 일단 낮은 값 비교를 보기 좋게하기 위해 오름차순으로 정렬하자.
A 1 4 7 10
B 3 7 8 15
A[0]=1의 값으로는 이길 수 없는 B팀이 없다.
A[1]=4로는 B팀의 B[0]3을 이길 수 있다. 점수 += 2- 여기서 분기점이 2개가 있다.
1) A[3]=10으로 B팀의 B[1]=7을 이긴다면 점수 += 2
2) A[2]=7로 B팀의 B[1]=7과 무승부를 한다면 점수 += 1
A[3]=10으로 B팀의 B[2]=8을 이긴다면 점수 += 1- 두 분기점의 차이는 A팀이 최대로 많이 승리하기 위해서는 A팀의 작은 값을 우선으로 B팀에서 이길 수 있는 값을 찾아야 한다.
- 또 하나 주의할 점이 있다.
A 3 4 5 6
B 1 2 5 7- 위와 같은 경우가 있을 때,
A[0]=3의 값으로 B[0]=1을 이기고, 점수 += 2
A[1]=4의 값으로 B[1]=2를 이기고, 점수 += 2
A[2]=5의 값으로 B[2]=5가 무승부이면, 점수 == 1, 총 점수는 5점이다.
A[0]=3의 값으로 B[1]=2를 이기고, 점수 += 2
A[1]=4의 값으로 B[0]=1을 이기고, 점수 += 2
A[3]=6의 값으로 B[2]=5를 이기면, 점수 += 2, 총 점수는 6점이 된다.- 즉 무승부보다 승리하는 것을 우선순위로 두어야 하고, 그러기 위해서는 의 값보다 작은 수 가 에서 존재한다면 존재하는 값 중 최댓값을 이겨야 나중에 최적의 승리가 가능해진다.
해답코드
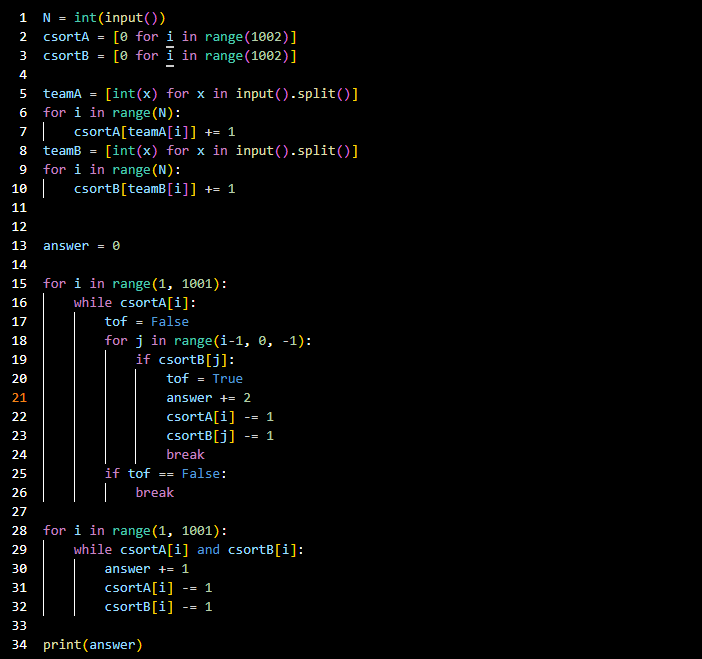
- 코드라인 1~10: 탐욕법을 이용한 예제 4와 같이 계수정렬을 사용했다.
- 코드라인 15: 1~1000까지의 범위를 순회하며, 계수
i에 해당하는csortA[i]가 (A팀) 존재한다면 - 코드라인 18~24:
i보다 작은 값k가 B팀에 존재한다면 그중 최댓값과 대결한다. - 코드라인 28~32: 무승부가 가능한 경우를 구해준다.
- 코드라인 34: 정답을 출력한다.
