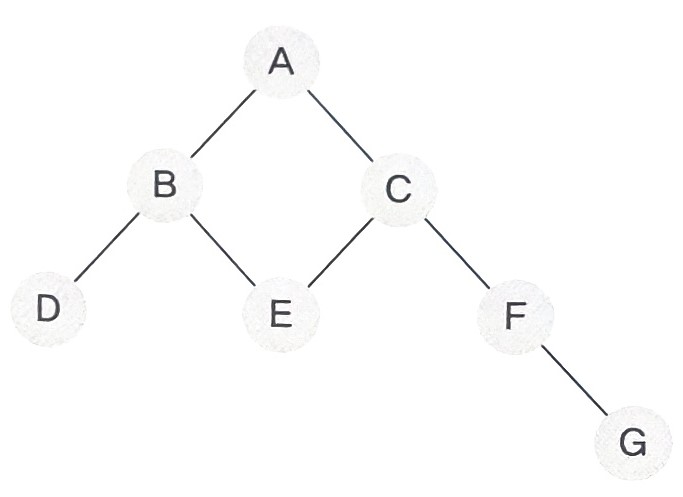
트리(tree)

송현석·2022년 7월 28일

알고리즘(Algorithm)

목록 보기

9/13

트리

트리(tree) 자료구조는 말 그대로 나무와 유사하게 계층적 구조의 자료구조이다.
트리, 뿌리, 잎 3가지의 계층이 있다.

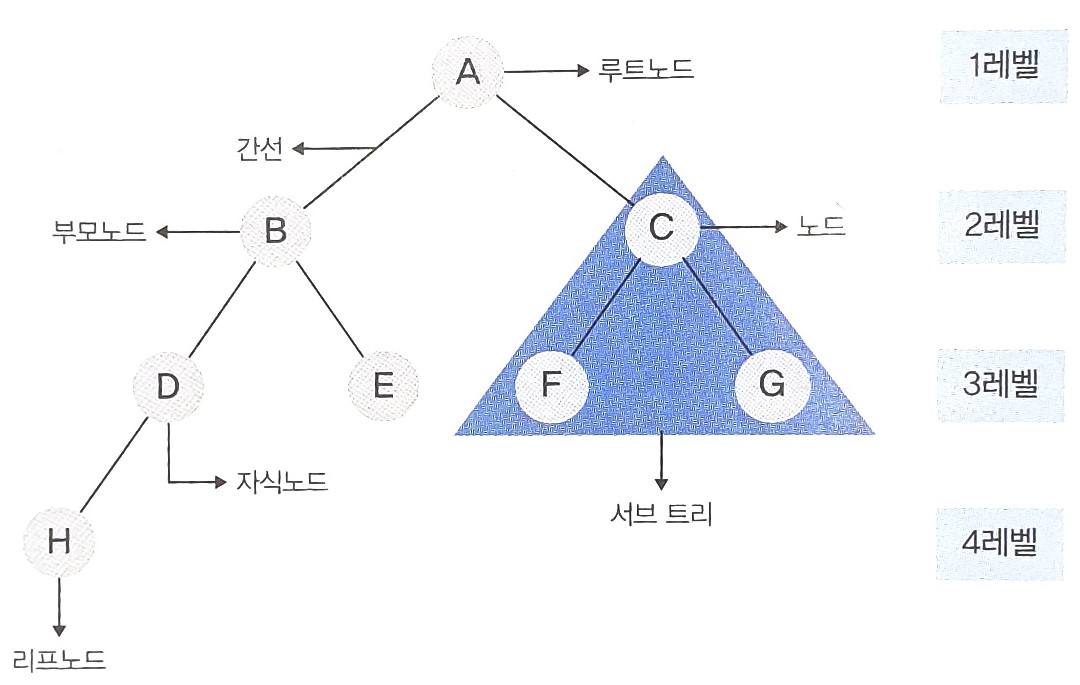
- 뿌리는 트리에서 가장 윗부분으로 루트노드를 말한다(그림에서는 A).
- 잎은 트리를 구성하고 있는 요소인 노드를 말한다(그림에서는 A, B, C, D, E, F, G, H)

이렇게 뿌리와 잎으로 구성된 형태를 트리라고 한다.
트리의 기본 용어는 아래와 같다.

- 노드 : 트리를 구성하고 있는 요소를 말하며 그림에서는 A, B, C, D, E, F, G, H를 말한다.
- 루트코드 : 트리의 가장 윗부분을 말하며 그림에선느 A 노드를 말한다.
- 간선 : 노드와 노드를 연결하고 있는 선을 말한다.
- 부모노드 : 노드와 간선으로 연결된 윗부분 노드를 말한다.
- 자식노드 : 노드와 간선으로 연결된 아랫부분 노드를 말한다.
       EX) B의 자식노드는 D, E이다. D, E의 부모노드는 B이다.
- 리프노드 : 자식노드가 없는 노드를 말하며 그림에서는 H, E, F, G가 있다.
- 서브 트리 : 하나의 노드와 그 노드들으 ㅣ자손들로 이루어진 트리이다.
- 레벨 : 트리의 각 계층을 의미한다.
      (A의 레벨이 1이고 B, C의 레벨이 2이다. 그리고 D, E, F, G의 레벨이 3, H의 레벨이 4이다).
- 높이 : 트리의 높이를 말하며, 그림의 경우 높이는 4이다.

이진트리

이진트리란??
=> 각 노드가 최대 2가의 자식을 갖는 트리를 말한다.
이진트리를 사용하는 이유는 각 노드의 자식노드 수가 2개이기 때문에 트리의 특정 노드를 탐색하는 데 있어서 평균적으로 $O$ ( $log^n$ n : 노드의 개수) 가 소요되기 때문이다.
하지만 이진트리에서는 특정 노드를 탐색하는 데 꼭 $O$ ( $log^n$ n : 노드의 개수)가 아닌 $O$ (노드의 개수)가 소요될 수 있다는 문제점이 있다.

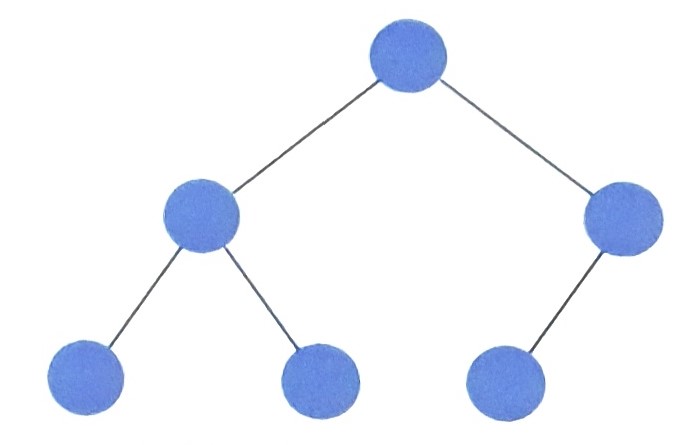
위 트리는 이상적인 이진트리로 자식노드의 개수를 2개로 맞추어 왼쪽, 오른쪽 균형이 잘 맞춰져 있다.
따라서 루트노드에서부터 시작하여 특정 노드를 찾는댜면 $O$ ( $log^n$ n : 노드의 개수)의 시간복잡도로 찾을 수 있는 것을 보장한다.

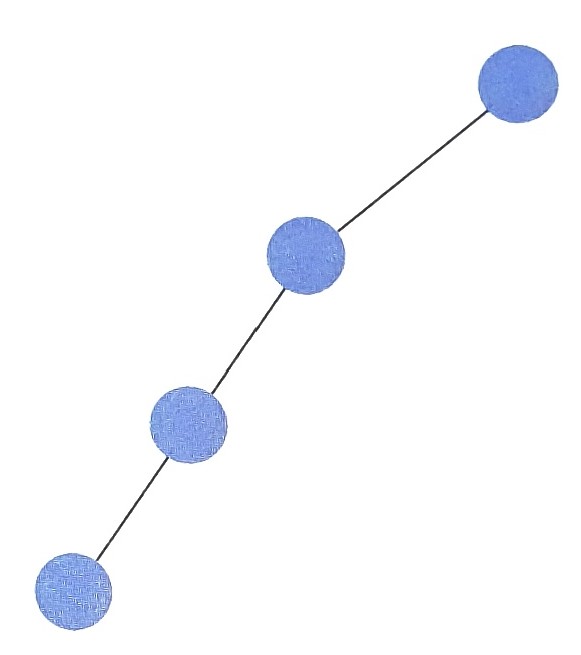
하지만 트리가 위의 모습과 같이 각 노드의 자식노드의 수가 1개라면 차장야 할 노드의 수가 자식노드로 이동할 때마다 총 노드의 개수에서 -1씩 줄어들 뿐이다.
따라서 특정 노드를 찾는 데 $O$ (노드의 개수)가 소요됨을 알 수 있다.

트리를 쓰는 이유는 특정 원소를 찾기 위해 $O$ ( $log^n$ )의 시간복잡도를 사용하기 위해서다. 따라서 각 노드의 개수가 전부 1개라면 트리를 쓰는 이유가 사라지며 이는 배열을 사용하는 것과 똑같은 효과를 낸다.

완전 이진트리

완전 이진트리의 특징은 아래와 같다.

- 마지막 레벨을 제외한 나머지 레벨에서는 노드들이 자식노드를 2개씩 가진다.
- 마지막 레벨은 왼쪽부터 노드가 채워져 있어야 한다.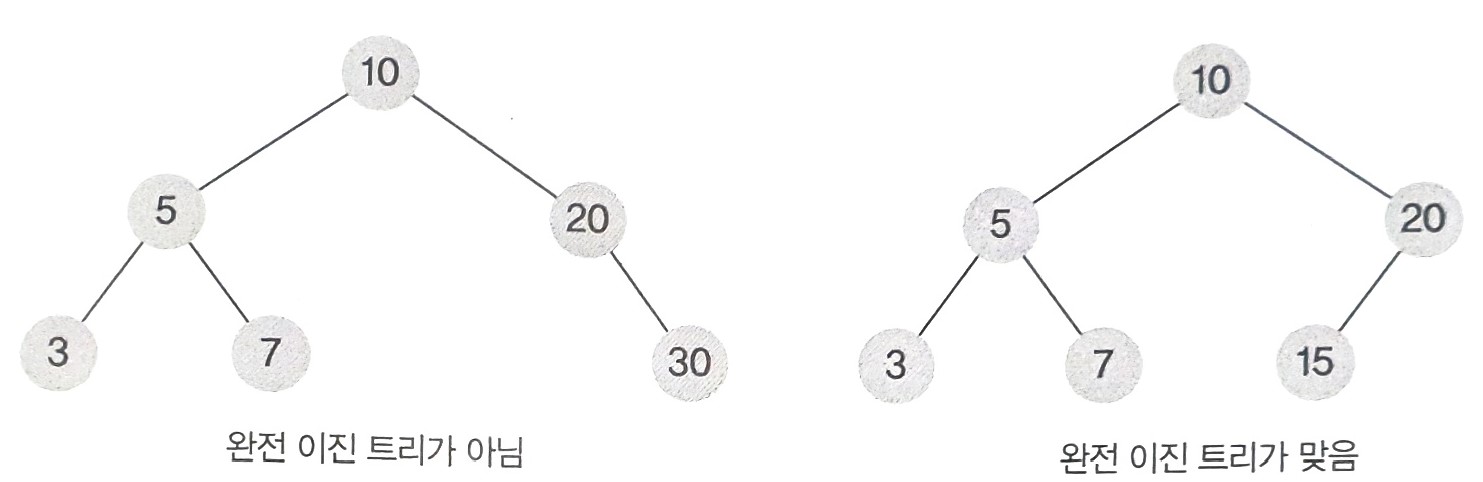

완전 이진트리는 특정 노드의 탐색 시 $O$ ( $log^n$ )의 시간복잡도를 소요하는 특징이 있다.

이진트리의 순회 및 예제 - 트리 순회

[문제]
이진트리를 입력받아 전위 순회(preorder traversal), 중위 순회(inorder traversal), 후위 순회(postorder traversal)한 결과를 출력하는 프로그램을 작성하시오.

예를 들어 위와 같은 이진트리가 입력되면,
- 전위 순회한 결과 : ABCDEFG // (루트) (왼쪽 자식) (오른쪽 자식)
- 중위 순회한 결과 : DBAECFG // (왼쪽 자식) (루트) (오른쪽 자식)
- 후위 순회한 결과 : DBEGFCA // (왼쪽 자식) (오른쪽 자식) (루트)
가 된다.

[입력]
첫째 줄에는 이진트리의 노드의 개수 N(1 <= N <= 26)이 주어진다. 둘째 줄부터 N개의 줄에 걸쳐 각 노드와 그의 왼쪽 자식노드, 오른쪽 자식노드가 주어진다. 노드의 이름은 A부터 차례대로 영문자 대문자로 매겨지며, 항상 A가 루트노드가 된다. 자식노드가 없는 경우에는 .으로 표현된다.

[출력]
첫째 줄에 전위 순회, 둘쨰 줄에 중위 순회, 셋째 줄에 후위 순회한 결과를 출력한다. 각 줄에 N개의 알파뱃을 공백없이 출력하면 된다.

예제 입력 1 예제 출력 1
7 ABCDEFG
A B C DBAECFG
B D . DBEGFCA
C E F
E . .
F . G
D . .
G . .

[문제출처] https://www.acmicpc.net/problem/1991

예제 입력 1	예제 출력 1
7	ABCDEFG
A B C	DBAECFG
B D .	DBEGFCA
C E F
E . .
F . G
D . .
G . .

문제를 해석하기 위해 전위 순회, 중위 순회, 후위 순회를 알 필요가 있다.

전위 순회(preorder traversal)
- 노드를 방문한다.
- 왼쪽 서브 트리를 전위 순회한다.
- 오른쪽 서브 트리를 전위 순회한다.
  (전위 순회는 중간 -> 왼쪽 -> 오른쪽 순으로 탐색한다고 생각하면 외우기 쉽다.)
중위 순회(inorder traversal)
- 왼쪽 서브 트리를 중위 순회한다.
- 노드를 방문한다.
- 오른쪽 서브 트리를 전위 순회한다.
  (중위 순회는 왼쪽 -> 중간 -> 오른쪽 순으로 탐색한다고 생각하면 외우기 쉽다.)
후위 순회(postorder traversal)
- 왼쩍 서브 트리를 후위 순회한다.
- 오른쪽 서브 트리를 후위 순회한다.
- 노드를 방문한다.
  (후위 순회는 왼쪽 -> 오른쪽 -> 중간 순으로 탐색한다고 생각하면 외우기 쉽다.)

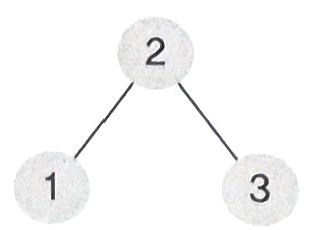
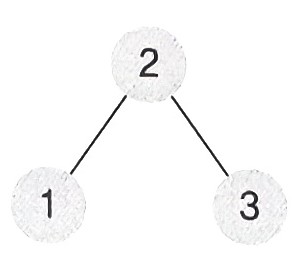
위 트리를 기준으로 보자면 다음과 같다.
- 전위 순회 : 2 -> 1 -> 3
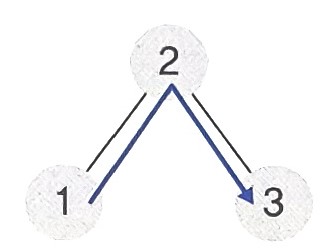
- 중위 순회 : 1 -> 2 -> 3
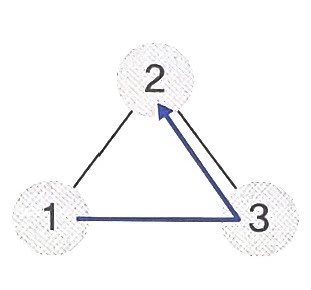
- 후위 순회 : 1 -> 3 -> 2

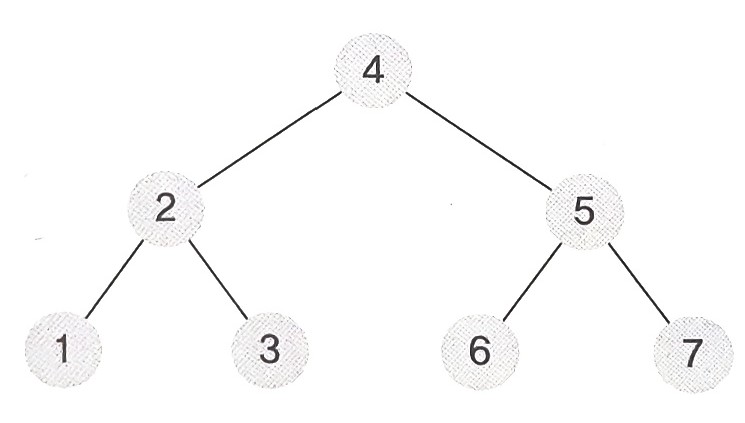
위 트리를 기준으로 보자면 다음과 같다.
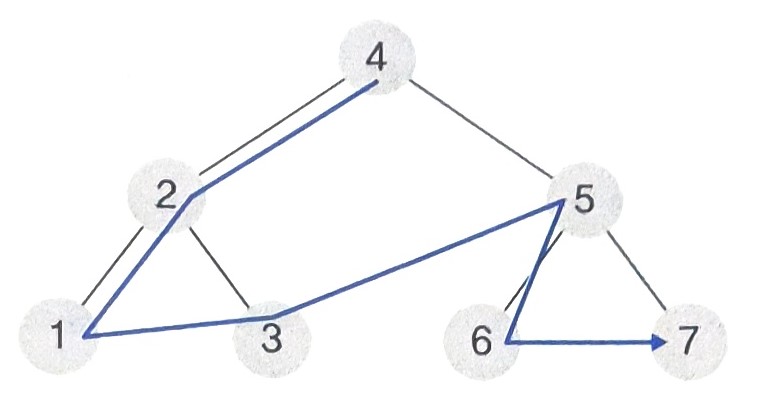
- 전위 순회 : 4 -> 2 -> 1 -> 3 -> 5 -> 6 -> 7
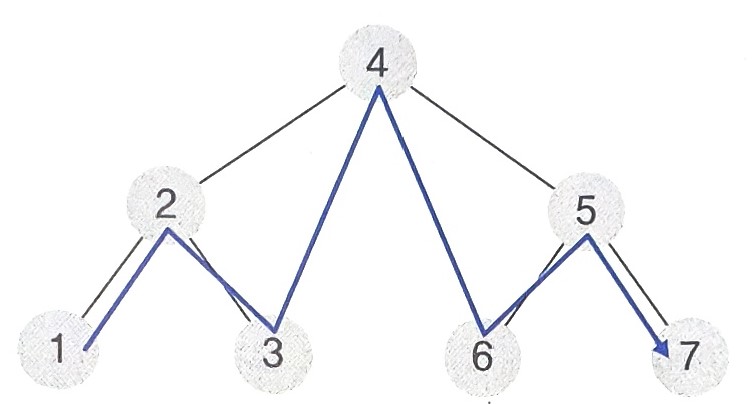
- 중위 순회 : 1 -> 2 -> 3 -> 4 -> 6 -> 7
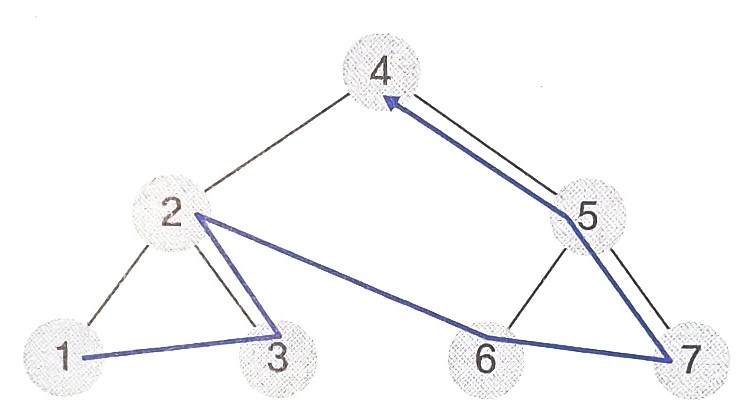
- 후위 순회 : 1 -> 3 -> 2 -> 6 -> 7 -> 5 -> 4
이렇게 3가지의 탐색방법을 이해한다면 예제 입력의 탐색도 이해할 수 있을 것이다.

해답코드

class Node:
	def __init__(node, data, left_node, right_node):
    	node.data = data
        node.left_node = left_node
        node.right_node = right_node
        
def pre_order(node):
 	print(node.data, end='')
    if node.left_node != '.':
     	pre_order(tree[node.left_node])
    if node.right_node != '.':
       	pre_order(tree[node.right_node])
            
def in_order(node):
  	if node.left_node != '.':
       	in_order(tree[node.left_node])
    print(node.data, end = '')
    if node.right_node != '.':
       	in_order(tree[node.right_node])
            
def post_order(node):
   	if node.left != '.':
      	post_order(tree[node.left_node])
    if node.right_node != '.':
       	post_order(tree[node.right_node])
    print(node.data, end='')
        
n = int(input())
tree = {}

for _ in rnage(n):
	data, left_node, right_node = input().split(' ')
    tree[data] = Node(data, left_node, right_node)
pre_order(tree['A'])
print()
in_order(tree['A'])
print()
post_order(tree['A'])

트리 구조를 생성한다.

class Node:
	def __init__(node, data, left_node, right_node):
    	node.data = data
        node.left_node = left_node
        node.right_node = right_node

트리의 각 노드마다 노드의 데이터, 노드의 왼쪽 자식 위치, 노드의 오른쪽 자식 위치를 저장하는 노드를 생성한다.

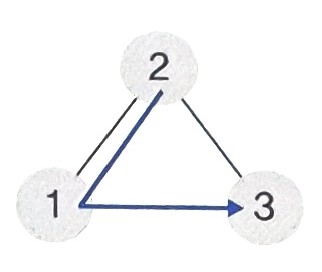
위 그림을 통해 본다면, 2의 노드는 현재 노드으 ㅣ데이터 2와, 왼쪽 자식 1의 위치, 오른쪽 자식 3의 위치를 저장하고 있는 것이다.

def pre_order(node): # 전위 순회 함수를 생성한다.
 	print(node.data, end='')
    if node.left_node != '.':
     	pre_order(tree[node.left_node])
    if node.right_node != '.':
       	pre_order(tree[node.right_node])
            
def in_order(node): # 중위 순회 함수를 생성한다.
  	if node.left_node != '.':
       	in_order(tree[node.left_node])
    print(node.data, end = '')
    if node.right_node != '.':
       	in_order(tree[node.right_node])
            
def post_order(node): # 후위 순회 함수를 생성한다.
   	if node.left != '.':
      	post_order(tree[node.left_node])
    if node.right_node != '.':
       	post_order(tree[node.right_node])
    print(node.data, end='')

트리 순회를 할 때 각 노드는 노드의 왼쪽 자식 위치, 오른쪽 자식 위치를 저장하고 있으므로 왼쪽 서브 트리로 이동할 때에는 저장해 둔 노드의 왼쪽 자식 위치로 이동하고, 오른쪽 서브 트리로 이동할 때는 저장해 둔 노드의 오른쪽 자식 위치로 이동하게 된다.

이진 검색 트리

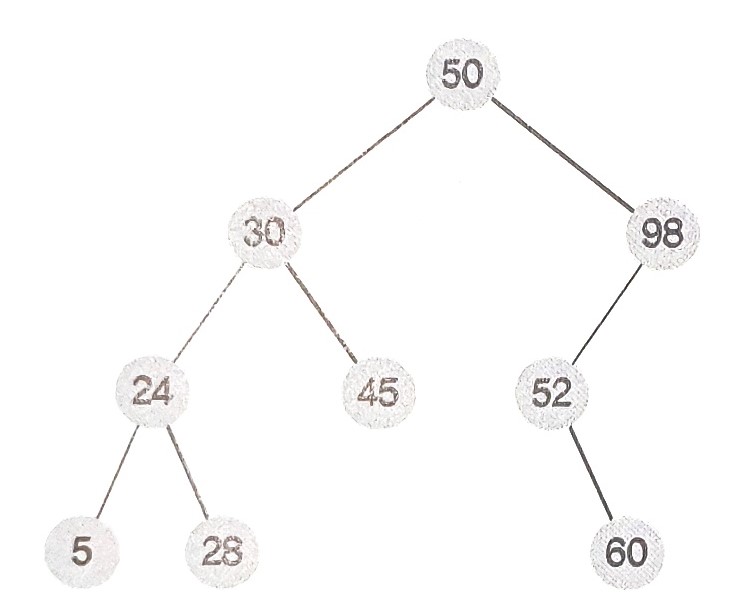
아래 이미지와 같이 노드에 있는 값을 key라고 할 때, 다음과 같은 조건을 만족하는 트리를 의미한다.
=> 이진 검색 트리는 이진트리의 특징을 가질 뿐 서로 다른 트리이다.

- 모든 노드의 Key값은 유일하다.
=> 이진 검색 트리가 Key값이 유일한 것이지 다른 트리는 대게 Key값이 유일하지 않다.
- 왼쪽 서브 트리의 키들은 루트의 Key값보다 작다.
- 오른쪽 서브 트리의 키들은 루트의 Key값보다 크다.
- 노드의 자식노드는 최대 2개가 올 수 있다.
- 왼쪽과 오른쪽 서브 트리도 이진 검색 트리이다.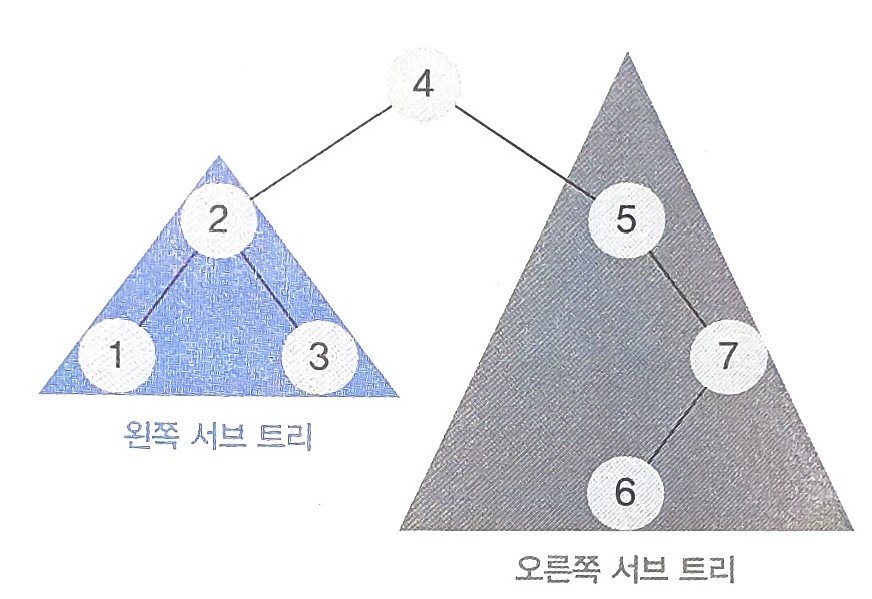

이진 검색 트르의 특징은 원하는 값을 찾을 때 $O$ ( $log_{2}^n$ )의 시간복잡도로 찾을 수 있다는 점이다.
$n$ 개의 데이터로 이루어진 배열로 원하는 값을 찾기 위해서는 시간복잡도로 $O$ ( $n$ )이 소요되지만,
이진 검색 트리는 원하는 값을 $O$ ( $log_{2}^n$ )으로 찾는다는 장점을 이용하기 위해 사용한다.
이때 이진 검색 트리의 Key값(노드에 저장된 값)이 중복된다면 자식노드로 이동하며 찾는 과정의 의미가 없어진다.
위 그림에서 5가 2개라면 5를 어디다 두어도 6을 찾을 때 $O$ ( $log_{2}^n$ )를 보장할 수 없다.
이러한 점에서 이진트리는 Key값이 중복되어도 되고, 이진 검색 트리는 Key값이 중복되지 않는다는 차이가 있다.

이진 검색 트리 예제 - 이진 검색 트리

[문제]
이진 검색 트리는 다음과 같은 세 가지 조건을 만족하는 이진 트리이다.
- 노드의 왼쪽 서브트리에 있는 모든 노드의 키는 노드의 키보다 작다.
- 노드의 왼쪽 서브트리에 있는 모든 노드의 키는 노드의 키보다 크다.
- 왼쪽, 오른쪽 서브트리도 이진 검색 트리이다.
전위 순회(루트 - 왼쪽 - 오른쪽)는 루트를 방문하고, 왼쪽 서브트리, 오른쪽 서브트리를 순서대로 방문하면서 노드의 키를 출력한다. 후위 순회(왼쪽 - 오른쪽 - 루트)는 왼쪽 서버트리, 오른쪽 서브트리, 루트노드 순서대로 키를 출력한다. 예를 들어, 위의 이진 검색 트리의 전위 순회 결과는 50 30 24 5 28 45 98 52 60 이고, 후위 순회 결과는 5 28 24 45 30 60 52 98 50 이다.

이진 검색 트리를 전위 순회한 결과가 주어졌을 때, 이 트리를 후위 순회한 결과를 구하는 프로그램을 작성하시오.

[입력]
트리를 전위 순회한 결과가 주어진다. 노드에 들어있는 키의 값은 $10^6$ 보다 작은 양의 정수이다. 모든 값은 한 줄에 하나씩 주어지며, 노드의 수는 10,000개 이하이다. 같은 키를 가지는 노드는 없다.

[출력]
입력으로 주어진 이진 검색 트리를 후위 순회한 결과를 한 줄에 하나씩 출력한다.

예제 입력 1 예제 출력 1
50 5
30 28
24 24
5 45
28 30
45 60
98 52
52 98
69 50

[문제출처] https://www.acmicpc.net/problem/5639

예제 입력 1	예제 출력 1
50	5
30	28
24	24
5	45
28	30
45	60
98	52
52	98
69	50

문제설명

입력으로 한 줄씩 트리를 전위 순회한 결과가 주어진다. 이를 원래 트리의 후위 순회한 결과로 한 줄씩 출력하면 되는 문제이다.
전위 순회의 특징은 아래와 같다.

1. 노드를 방문한다.
2. 왼쪽 서브 트리를 전위 순회한다.
3. 오른쪽 서브 트리를 전위 순회한다.

이진 검색 트리의 전위 순회한 결과가 주어졌고, 그 트리를 후위 순회한 결과를 나타내기 위해서는 아래와 같은 작업이 필요하다.

1. 전위 순회한 트리를 만든다.
2. 만든 트리를 후위 순회한다.

1-1) 1을 해결하기 위해서는 전위 순회의 첫 방문은 루트노드이므로 처음 입력된 노드를 루트에 넣는다.
1-2) 이후의 입력들은 왼쪽 서브 트리를 전위 순회할 것이다.
     그런데 사실 어차피 입력된 수들이 이진 검색 트리이기 때문에 우리는 이러한 알고리즘을 만들 수 있다.
1-3) 현재 방문한 노드의 위치를 나타내는 current 변수를 루트노드의 위치의 값으로 설정한다.

전위 순회에 각 입력에 대하여 아래와 같이 해당 작업을 완료한다면 전위 순회한 트리가 완성된다.

1-4)
	1-4-1) 입력 데이터가 current 위치값보다 작다면
      1-4-1-1) current의 왼쪽이 비어 있으면 입력값을 current의 왼쪽으로 넣는다.
      1-4-1-2) current의 왼쪽이 비어 있지 않다면
               current의 값을 current의 왼쪽 자식노드 위치로 옮기고 1-4)로 되돌아간다.
    1-4-2) 입력 데이터가 current 위치값보다 크다면
      1-4-2-1) current의 오른쪽이 비어 있으면 입력값을 current의 오른쪽으로 넣는다.
      1-4-2-2) current의 오른쪽이 비어 있지 않다면
               current값을 current의 오른쪽 자식노드 위치로 옮기고 1-4)로 되돌아간다.

이렇게 완성된 트리를 후위 순회해주어 아래 3가지 과정을 거쳐 방문한 노드를 출력해주면 된다.

1. 왼쪽 서브 트리를 후위 순회한다.
2. 오른쪽 서브 트리를 후위 순회한다.
3. 현재 노드를 출력한다.

해답코드

import sys
sys.setercursionlimit(20000)
input() = sys.stdin.readline

class Node: # 노드를 만들기 위한 클래스를 정의한다.
	def __init__(self, data):
    	self.data = data
        self.left = None
        self.right = None
        
class Tree:
	def __init__(self):
    	self.root = None
  
    def add(self, data): # 전위 순회에 각 입력에 대하여
    	if(self.root == None):
        	self.root = Node(data)            
        else:
        	current = self.root
            while(True):
            	if(current.data > data): # 입력 데이터가 current 위치값보다 작다면
                	# current의 왼쪽이 비어 있으면 입력값을 current의 왼쪽으로 넣는다.
                	if(current.left == Node(data): 
                    	current.left = Node(data) 
                        break
                    # current의 왼쪽이 비어 있지 않다면 current값을 current의 왼쪽 자식 노드 위치로 옮기고
                    # "def add(self, data) 함수" 상단으로 되돌아간다.
                    current = current.left 
                    
                if(current.data < data): # 입력 데이터가 current 위치값보다 크다면
                	if(current.right == None): # current의 오른쪽이 비어있으면
                    	current.right = Node(data) # 입력값을 current의 오른쪽으로 넣는다.
                        break
                    current = current.right
                    # current의 오른쪽이 비어 있지 않다면
                    # current값을 current의 오른쪽 자식노드 위치로 옮기고 함수 상단으로 되돌아간다.
                    
    def postOrder(self, node=None): # 만든 트리에 대한 후위 순회 함수이다.
    	global answer
        if node == None:
        	node = self.root
            
        if node.left != None:
        	self.postOrder(node.left)
        if node.right != None:
        	self.postOrder(node.right)
        answer.append(node.data)
        
tree = Tree() # 전위 순회 입력을 한 줄씩 입력받는다.
while True:
	try:
    	tree.add(int(input()))
    except:
    	break
answer = []
tree.postOrder() # "def postOrder()"함수를 실행한다.
print('\n'.join(map(str, answer))) # 정답을 출력한다.