맵

송현석·2022년 8월 1일

python 기초

알고리즘(Algorithm)

목록 보기

10/13

맵(Map)??

맵(Map)은 데이터를 Key-Value(키-값)의 형식으로 저장하는 방식이다. Key는 중복을 허용하지 않지만, Value는 중복을 허용한다는 특징이 있다.

트리를 이용하여 구현하는 맵

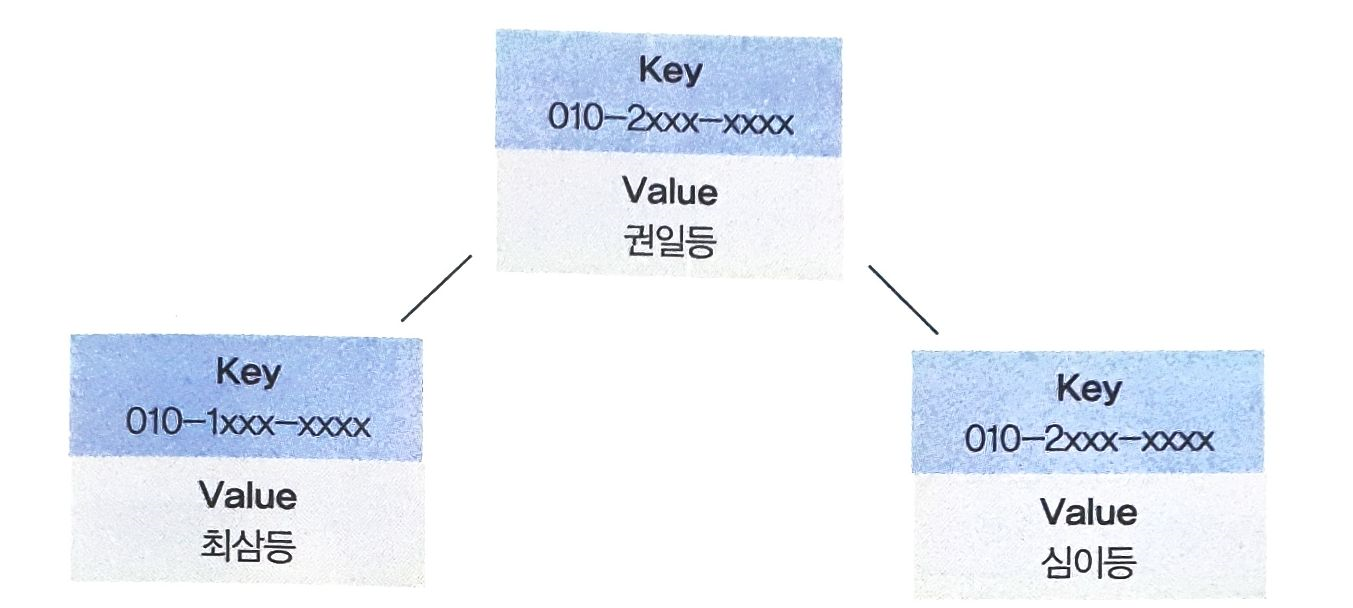
완전 이진 검색 트리의 각 노드에 Key와 Value를 저장하는 데이터를 추가한다면 맵 자료구조를 완성할 수 있다.
이때 원하는 값을 찾을 때 $O(\log_{2}n)$ 의 시간복잡도로 찾을 수 있으며 트리에 값을 추가할 때도 $O(\log_{2}n)$ 의 시간복잡도로 삽입할 수 있다.
완전 이진 검색 트리의 데이터 추가는 시간복잡도가 $O(\log_{2}n)$ 이 아니다.
실제로는 레드블랙 트리를 이용하여 데이터 추가의 시간복잡도가 $O(\log_{2}n)$ 가 되지만 여기서는 편의상 이해하기 쉽게 완전 이진 검색 트리 구조에 각 노드를 Key-Value 형태로 저장해둔 모습이라 하겠다.

해시를 이용하여 구현하는 맵

해시를 이용한 맵은 해시(다양한 길이를 가진 데이터를 고정된 길이를 가진 데이터로 변경한 값)화한 Key를 통해 Key-Value를 저장해둔 자료구조이다.
여기서 해시화를 해싱(Hashing)이라 부르겠다.
해싱이란 Key값이 주어졌을 때 항상 동일한 해시값을 보장해주는 방식을 의미한다.
숫자1, 2, 3, 4, 5가 있고 입력된 숫자를 3으로 나눈 나머지 값으로 해싱을 설정한다고 할때, 그에 대한 해시값은 아래와 같다.

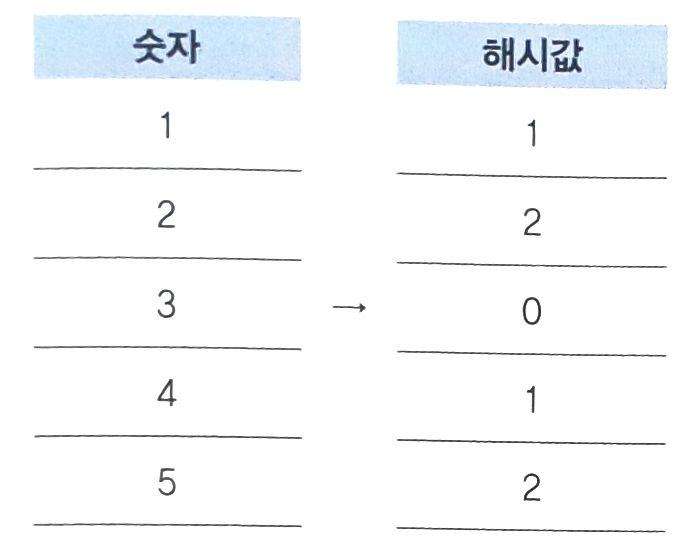
숫자 1을 해싱에 입력한다면 해시값은 항상 1이 나오며,
숫자 3을 해싱에 입력한다면 해시값은 항상 0이 나오며,
숫자 4를 해싱에 입력한다면 해시값은 항상 1이 나온다.

해싱을 1,000,000,000으로 나눈 나머지로 한다면 10억 이하의 수는 모두 다른 해시값을 가질 것이다.
이렇게 중복되지 않은 해시값을 통해 Key값을 저장할 메모리 위치를 확보하며 Value값을 넣어준다.
문제는 해싱을 10억으로 나눈 나머지로 설정한다면 메모리를 매우 많이 차지할 수 있는 반면(숫자형 변수 10억 개의 메모리 크기는 대략 4GB이다). 해싱을 3으로 나눈 나머지로 설정한다면 중복되는 해시값이 발생할 수 있다.
이러한 문제점을 해결하기 위해 체이닝, 오픈 어드레싱 방법을 사용한다.

체이닝 방식

동일한 해시값으로 인한 해시 충돌이 발생할 경우 동일한 해시값에 해당하는 Key끼리 서로 연결해가며 저장해둔 방식이다.

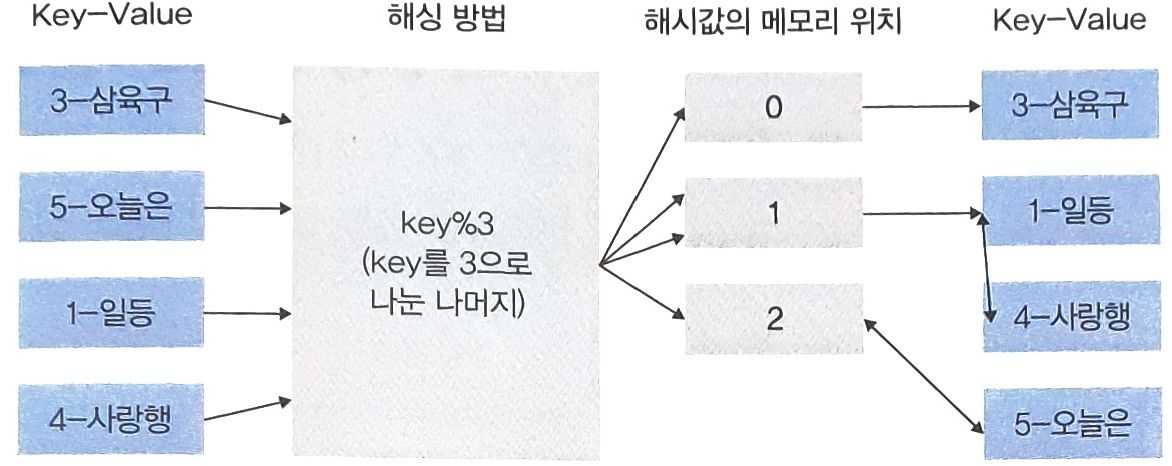
해싱을 Key값 3으로 나눈 나머지로 설정했을 때

'1-일등'은 메모리 1에, (1 % 3 = 1)
'3-삼육구'는 메모리 0에. (3 % 3 = 0)
'4-사랑행'은 메모리 1에, (4 % 3 = 1)
'5-오늘은'은 메모리 2에 위치시킨다 (5 % 3 = 2)

'1-일등'과 '4-사랑행'은 해시값이 같기 때문에, LinkedList 자료구조를 이용하여 해시값의 메모리 위치에 Key-Value 데이터를 하나씩 추가해서 서로 연결해가며 저장해 둔다.
이러한 체이닝 방법은 동일한 Key값(동일한 Key값은 결국 해시값도 동일하다)을 가지는 곳에 Value를 저장하기 위해 알맞은 구조이다.

SNS중 인스타그램에는 해시 태그라는 기능이 있다. 해시 태그는 '#문자'에 해당하는 Key에 게시글 Value를 저장한다.
해싱 방법을 이용하여 인스타그램 해시 태그를 구현할 수 있고, 그렇게 구현했을 경우, 시간복잡도는 평균적으로 Key를 해시화하는 시간복잡도 $O(1)$ 로 게시글을 저장한 곳으로 이동할 수 있다.
단, 해시값의 위치에 연결된 데이터가 많다면 최대 $O(n)$ 의 시간복잡도가 소요된다.

오픈 어드레싱 방식

해시값에 해당하는 메모리 위치에 Key-Value가 있다면 그 위치부터 탐색해가며 아무 값도 없는 위치에 Key-Value를 넣는 방식이다.

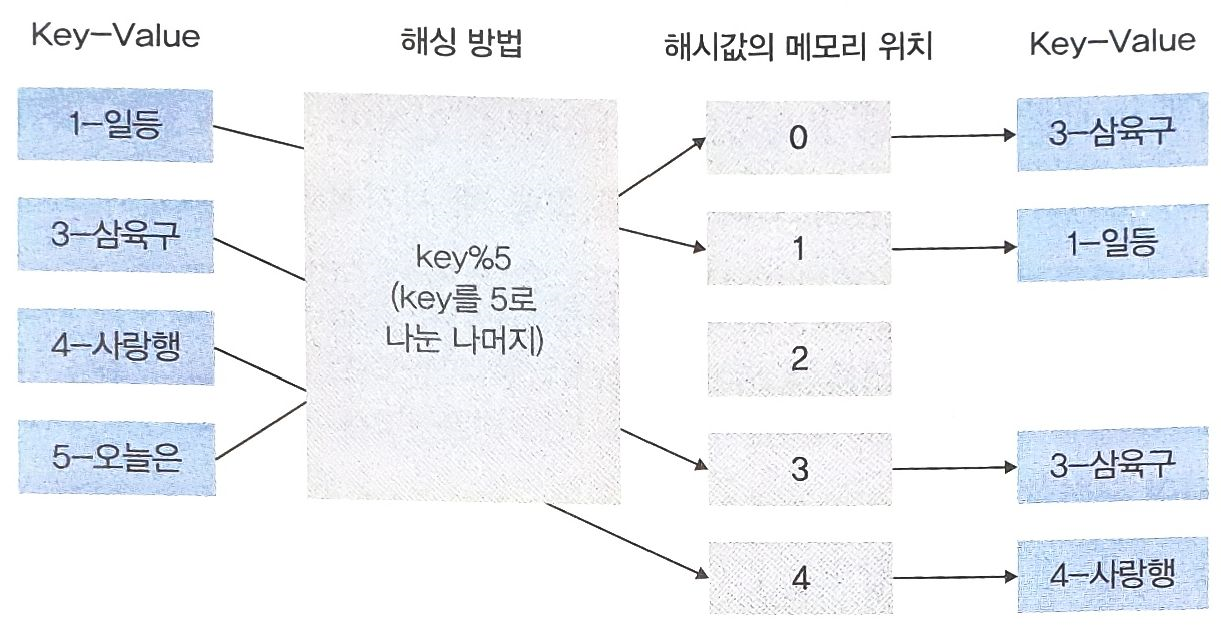
Key값을 5로 나눈 나머지로 해싱을 설정했을 때

'1-일등'은 메모리 1에, (1 % 5 = 1)
'3-삼육구'는 메모리 3에, (3 % 5 = 3)
'4-사랑행'은 메모리 4에, (4 % 5 = 4)
'5-오늘은'은 메모리 0에 위치시킨다. (5 % 5 = 0)

이때 다음 그림처럼 '6-육개장'이라는 Key-Value를 추가할 때 Key의 해시값은 0이므로 메모리 0부터 탐색해가며 Key값이 들어있지 않은 2번 위치에 Key-Value를 넣어주면 된다.

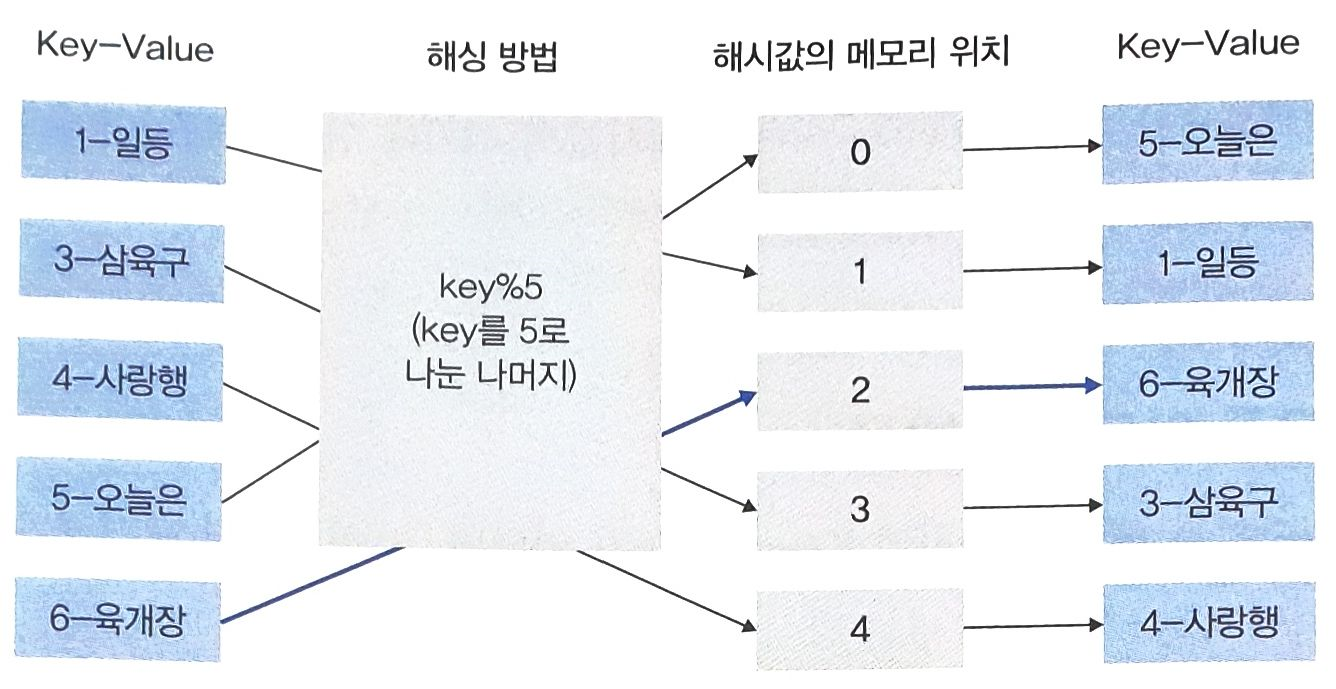
오픈 어드레싱 방식은 메모리를 효율적으로 사용할 수 있지만,
단점으로는 최악의 경우 해시값의 충돌이 일어나 비어 있는 메모리 위치를 찾을 때 시간복잡도는 $O$ (메모리의 크기)가 된다.
그렇지만 평균적으로 $O(1)$ 의 시간복잡도를 보장해준다.
마지막으로, 시간복잡도를 정리하면
- 트리를 이용하여 구현한 맵
  원하는 값을 찾을 때 시간복잡도는 $O(\log_{2}n)$ 이며, Value를 추가할 때의 시간복잡도는 $O(\log_{2}n)$ 이다.
- 해시를 이용하여 구현한 맵
  원하는 값을 찾을 때 평균 시간복잡도는 $O(1)$ 이며, Value를 추가할 떄의 평균 시간복잡도는 $O(1)$ 이다.

맵을 사용하는 예제1 - 패션왕 신해빈

파이썬에서 맵은 dictionary라는 내장 자료구조를 이용하면 된다.
[문제]
해빈이는 패션에 매우 민감해서 한번 입었던 옷들의 조합을 절대 다시 입지 않는다. 예를 들어 오늘 해빈이가 안경, 코트, 상의, 신발을 입었다면, 다음날은 바지를 추가로 입거나 안경대신 렌즈를 착용하거나 해야한다. 해빈이가 가진 의상들이 주어졌을때 과연 해빈이는 알몸이 아닌 상태로 며칠동안 밖에 돌아다닐 수 있을까?

[입력]
첫째 줄에 테스트 케이스가 주어진다. 테스트 케이스는 최대 100이다.
- 각 테스트 케이스의 첫째 줄에는 해빈이가 가진 의상의 수 n(0 <= n <= 30)이 주어진다.
- 다음 n개에는 해빈이가 가진 의상의 이름과 의상의 종류가 공백으로 구분되어 주어진다. 같은 종류의 의상은 하나만 입을 수 있다.
모든 문자열은 1이상 20이하의 알파벳 소문자로 이루어져 있으며 같은 이름을 가진 의상은 존재하지 않는다.

[출력]
각 테스트 케이스에 대한 해빈이가 알몸이 아닌 상태로 의상을 입을 수 있는 경우를 출력하시오.

예제 입력1 예제 출력1
2 5
3 3
hat headgear
sunglasses eyewear
turban headgear
3
mask face
sunglasses face
makeup face

예제 입력1	예제 출력1
2	5
3	3
hat headgear
sunglasses eyewear
turban headgear
3
mask face
sunglasses face
makeup face

문제설명

각 테스트 케이스마다, 해빈이가 가진 의상의 수 n이 주어지며, 입력은 의상의 이름, 의상의 종류로 주어진다. 이때 같은 종류의 의상은 하나만 입을 수 있다. 이를 해결하기 위해 경우의 수와 맵을 이용해야 하는 문제이다.

의상의 이름	의상의 종류
hat	headgear
sunglasses	eyewear
turban	headgear

예제 입력1의 테스트 케이스를 보며 설명하면, 결과적으로 정답을 내기 위해서 혜빈이는 의상의 종류는 중복이 되면 안 되게 입을 수 있는 경우의 수를 모두 구해야 한다.
혜빈이가 입을 수 있는 옷 종류의 경우는 다음과 같이 3가지가 있다.

- headgear만 입는 경우
- eyewear만 입는 경우
- headgear, eyewear를 동시에 입는 경우

headgear에서 택할 수 있는 경우는 hat, turban, 선택 안함. 3가지가 있고, eyewear에서 택할수 있는 경우는 sunglasses, 선택 암함. 2가지가 있다.
headgear에서 가능한 경우 $_3C_1 = 3$ 과 everywear에서 가능한 경우 $_2C_1 = 2$ 를 곱해준 후 옷을 전부입지 않은 상태를 뺴주면 정답이 된다.

3 * 2 - 1 = 5

정답으로 도식화하면 아래의 식과 같다.

정답 = (의상 종류 1에서 선택 가능한 수 + 1) * (의상 종류 2에서 선택 가능한 수 + 1) * ...
	  * (의상 종류 n에서 선택 가능한 수 + 1) -1(옷을 입지 않은 경우)

의상의 이름은 중요하지 않고 의상의 종류에 의상의 이름이 몇 개가 있는지가 중요한 문제이다.
이를 위해서 의상의 종류룰 Key로 두고 해당 의상의 종류와 짝이 맞는 의상의 이름이 나올 때마다 Value값을 1씩 증가시키면 의상의 종류에는 몇 개의 의상이 이름이 있는지 알 수 있다.

해답코드

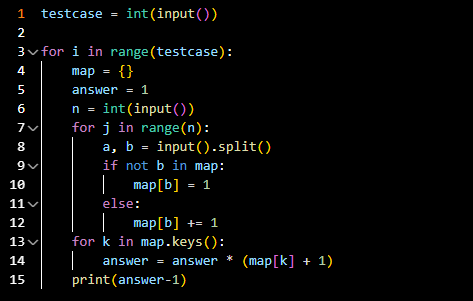
코드라인 4: map을 사용하기 위해 변수명 = {} 을 사용한다.
코드라인 6: 의상의 수 n을 입력받는다.
코드라인 8: 의상의 이름, 의상의 종류를 입력받는다.
코드라인 9~10: 의상의 종류를 key로 하는 값이 map에 없다면 key에 해당하는 value를 1로 설정해준다.
			map[key] += 1 이다.
코드라인 13~14: map 안에 있는 모든 key를 순회하며 정답을 출력할 변수에 key에 해당하는 (value+1) 값을
			  곱해준다. 이는 '의상의 종류'에서 선택 가능한 수 +1 이다.
코드라인 15: 옷을 전부 입지 않은 값을 포함하므로 정답에서 -1을 뺀 값을 출력해준다.

맵을 사용하는 예제 2 <코드포스> - Non-zero Segments

Kolya got an integer array $a_1, a_2, ... , a_n$ . The array can contain both positive and negative integers. but Kolya dosen`t like 0. so the array doesn`t contain any zeros.

Kolya doesn`t like that the sum of some subsegments of his array can be 0. The subsegment is some consecutive segment of elements of the array.

You have to help Kolya and change his array in such a way that it doesn`t contain any subsegments with the sum 0. To reach this goal, you can insert any integers between any pair of adjacent elements of the array (integers can be really any: postive, negative, 0. any by absolute value. even such a huge that they can`t be represented in most standard programming languages).

Your task is to find the minimum number of integers you have to insert into Kolya`s array in such a way that the resulting array doesn`t contain any subsegments with the sum 0.

[Input]
The first line lf the input contains one integer $n(2 <= n <= 200000)$ - the number of elements in Kolya`s array.

[Output]
Print the minimum number of integers you have to insert intl Kolya`s array in such a way that the resulting array doesn`t contain any subsegements with the sum 0.

input 1 output 1
4 1
1 -5 3 2

input 2 output 2
5 0
4 -2 3 -9 2

input 3 output 3
9 6
-1 1 -1 1 -1 1 1 -1 -1

input 4 output 4
8 3
16 -5 -11 -15 10 5 4 -4

input 1	output 1
4	1
1 -5 3 2

input 2	output 2
5	0
4 -2 3 -9 2

input 3	output 3
9	6
-1 1 -1 1 -1 1 1 -1 -1

input 4	output 4
8	3
16 -5 -11 -15 10 5 4 -4

문제설명

0을 제외한 양의 정수와 음의 정수로 구성된 배열이 있다.
이배열의 연속 부분들의 합이 0이 되는것을 방지하기 위해 당신은 원하는 수(0혹은 무한도 가능)를 배열 사이에 삽입할 수 있다.
배열의 연속 부분들의 합이 0이 없도록 하기 위해 수를 삽입해야 하는 최소 횟수를 구하면 된다.
input 4를 보면,

n = 8
배열 a = 16, -5, -11, -15, 10, 5, 4, -4

연속된 합이 0이 되는 부분을 확인해보면

a[0] = 16을 만났을 때, 누적합은 16이다.
a[1] = -5를 만났을 때, 누적합은 11이다.
a[2] = -11을 만났을 때, 누적합은 0이다.
이때 -5와 -11 사이에 무한을 넣어주면 연속된 합이 0이 되지 않는다.

a[3] = -15를 만났을 때, 누적합은 -15가 된다.
a[4] = 10을 만났을 때, 누적합은 -5가 된다.
a[5] = 5를 만났을 때, 누적합은 0이 된다.
이때 10과 5 사이에 무한을 넣어주면 연속된 합이 0이 되지 않는다.

a[6] = 4를 만났을 때 누적합은 4가 된다.
a[7] = -4를 만났을 때 누적합은 0이 된다.
이때 4와 -4 사이에 무한을 넣어주면 연속된 합이 0이 되지 않는다.

총 3가지의 경우 0이 연속된 배열의 합이 0이 될 수 있다.
이는 누적합 개념과 맵 자료구조를 사용하면 해결할 수 있다.

해답코드

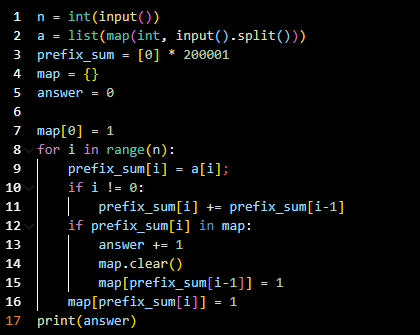
코드라인 1: n을 입력받는다.
코드라인 2: 배열 a를 입력받는다.
코드라인 3: 누적 합을 이용하기 위한 배열을 생성한다.
코드라인 7~16: 자료구조 map을 사용한다.
	코드라인 7: map[0] = 1로 초기화 해두었다.
    		이는 코드라인 12에서 수를 삽입해야 하는 연속된 배열의 합이 0일 때를 확인하기 위해서이다.
	코드라인 8: 배열을 탐색하기 위해 for문을 사용한다.
    코드라인 9~11: 누적 합 사용을 위해 누적 합 - 이전 합 + 현재 합의 방정식을 통해 구해준다.
    코드라인 12~15: 누적 합에 해당하는 key값이 map에 있다면 정답의 개수를 1 증가하고, map자료구조를 초기화
    			해준다. 그 후 무한을 삽입한 다음 누적 합부터 다시 수를 삽입해야 하는 연속된 배열의 합이 0일
                때를 확인하기 위해 map[prefix_sum[i-1]]=1로 값을 설정해준다.
	코드라인 16: 누적 합이 map 자료구조에 있음을 표시해 준다.
코드라인 17: 정답을 출력한다.

맵을 사용하는 예제 3 <코드포스> - MEX maximizing

Recall that MEX of an array is a minimum non-negative integer that does not belong to the array.
Examples:
- for the array [0, 0, 1, 0, 2] MEX equals to 3 because numbers 0, 1 and 2 are presented in
  the array and 3 s th minimum non-negative integer not presented in the array;
- for the array [1, 2, 3, 4] MEX equals to 0 because 0 is the minimum non-negative integer
  not presented in the array;
- for the array [0, 1, 4, 3] MEX equals to 2 because 2 is the minimum non-negative integer
  not presented in the array.
You are given an empty array $a$ =[ ] (in other words, a zero-length array). You are also given a positive integer $x$ .

You are also given $q$ queries. The $j-$ th query consists of one integer $y_j$ and means that you have to append one element $y_j$ to the array. The array length increases by 1 after a query.

In one move, you can choose any index $i$ and set $a_i := a_i + x$ or $a_i := a_i - x$ (i.e. increase or decrease any element of the array by $x$ ). The only restriction is that $a_i$ cannot become negative. Since initially the array is empty. you can perform moves only after the first query.

You have to maximize the MEX (minimum excluded) of the array if you can perform any number of such operations (you can even perform the operation multiple times with one element).

You have to find the answer after each of $q$ queries (i.e. the $j-$ th answer corresponds to the array of length $j$ ).

Operations are discarded before each query. l.e. the array a after the $j-$ th query equals to
[ $y_1, y_2, ..., y_i$ ].

[Input]
The first line of the input contains two integers $q$ , $x$ (1 <= q, x <= 4 · $10^9$ ) - the number of queres and the value of $x$ .

[Output]
Print the answer to the initial problem after each query - for the query $j$ print the maxmum value of MEX after first $j$ queries. Note that queries are dependent (the array changes after each query) but operations are independent between queries.

input 1 output 1
7 3 1
0 2
1 3
2 3
2 4
0 4
0 7
10

input 2 output 2
4 3 0
1 0
2 0
1 0
2

[Note]
In the first example:
- After the first query, the array is a=[0]
  : you don`t need to perform any operations, maximum possible MEX is 1.
- After the second query, the array is a=[0, 1]
  : you don`t need to perform any operations, maximum possible MEX is 2.
- After the third query, the array is a=[0, 1, 2]
  : you ton`t need to perform any operations, maximum possible MEX is 3.
- After the fourth query, the array is a=[0, 1, 2, 2]
  : you don`t need to perform any operations, maximum possible MEX is 3
   (you can`t make it greater with operations).
- After the fifth query, the array is a=[0, 1, 2, 2, 0]
  : you can perform a[4]:=a[4]+3=3.
   array change to be a=[0, 1, 2, 2, 3].
   Now MEX is maximum possible and equals to 4.
- After the sixth query, the array is a=[0, 1, 2, 2, 3, 0]
  : you can perform a[4]:=a[4]+3=0+3=3.
   The array changes to be a=[0, 1, 2, 2, 3, 0].
   Now MEX is maximum possible and equals to 4.
- After the sebenth query, the array is a=[0, 1, 2, 2, 0, 0, 10]
  You can perform the following operations:
    a[3]:=a[3]+3=2+3=5
    a[4]:=a[4]+3=0+3=3
    a[5]:=a[5]+3=0+3=3
    a[5]:=a[5]+3=3+3=6
    a[6]:=a[6]-3=10-3=7
    a[6]:=a[7]-3=7-3=4
  The resulting array will be a=[0, 1, 2, 5, 3, 6, 4].
  Now MEX is maximum possible and equals to 7.

input 1	output 1
7 3	1
0	2
1	3
2	3
2	4
0	4
0	7
10

input 2	output 2
4 3	0
1	0
2	0
1	0
2

문제설명

mex란 배열에서 배열에 없는 수 중에서 0 이상의 수 중 가장 작은 값을 말한다.
예를 들어,

배열=[0, 0, 1, 0, 2]의 mex 값은 3이다. 배열에 0, 1, 2 다음 3이 없기 때문이다.
배열=[1, 2, 3, 4]의 mex 값은 0이다. 배열에 0이 없기 때문이다.
배열=[0, 1, 4, 3]의 mex 값은 2이다. 배열에 0, 1 다음 2가 없기 때문이다.

$q$ 와 $x$ 가 입력으로 들어온다.
또한 $q$ 번 동안 $y$ 가 입력으로 들어오는데, $y$ 가 들어올 때마다, 배열 $a$ 에 $y$ 를 넣어준다.
그 후 배열 $a$ 안에 있는 수를 $a_i=a_i+x$ , $a_i=a_i-x$ ( $0<=i<$ 배열의 크기) 둘 중 한 가지 작업으로 여러번 바꿔줄 수 있다(단 $a_i$ 가 0보단 작을 순 없다).
$q$ 번의 입력마다 배열 $a$ 에서 만들 수 있는 최대 mex값을 출력하는 것이다.
input 1을 보자. => q=7, x=3
- $y_0$ =0이 입력으로 들어오면 배열 $a$ 의 상태는 $a$ =[0]이 된다.
  - 만들 수 있는 최대 mex값=1 이다.
- $y_1$ =1이 입력으로 들어오면 배열 $a$ 의 상태는 $a$ =[0, 1]이 된다.
  - 만들 수 있는 최대 mex값=2 이다.
- $y_2$ =0이 입력으로 들어오면 배열 $a$ 의 상태는 $a$ =[0, 1, 2]이 된다.
  - 만들 수 있는 최대 mex값=3 이다.
- $y_3$ =1이 입력으로 들어오면 배열 $a$ 의 상태는 $a$ =[0, 1, 2, 2]이 된다.
  - 만들 수 있는 최대 mex값=3 이다.
- $y_4$ =0이 입력으로 들어오면 배열 $a$ 의 상태는 $a$ =[0, 1, 2, 2, 0]이 된다.
  - $a$ [4]= $a$ [4] + ( $x$ =3) 으로 작업을 한 번 해주어 $a$ =[0, 1, 2, 2, 3] 으로 만들자.
  - 만들 수 있는 최대 mex값=4 이다.
- $y_5$ =0이 입력으로 들어오면 배열 $a$ 의 상태는 $a$ =[0, 1, 2, 2, 2, 0]이 된다.
  - $a$ [4]= $a$ [4] + ( $x$ =3) 으로 작업을 한 번 해주어 $a$ =[0, 1, 2, 2, 3, 0] 으로 만들자.
  - 만들 수 있는 최대 mex값=4 이다.
- $y_6$ =0이 입력으로 들어오면 배열 $a$ 의 상태는 $a$ =[0, 1, 2, 2, 2, 0, 10]이 된다.
  - $a$ [3] = $a$ [3]+3 = 2+3 = 5
  - $a$ [4] = $a$ [4]+3 = 0+3 = 3
  - $a$ [5] = $a$ [5]+3 = 0+3 = 3
  - $a$ [5] = $a$ [5]+3 = 3+3 = 6
  - $a$ [6] = $a$ [6]-3 = 10-3 = 7
  - $a$ [6] = $a$ [6]-3 = 7-3 = 4 로 작업을 해주어 $a$ =[0, 1, 2, 5, 3, 6, 4]로 만들자.
문제가 이해됬다면 해결할 방법을 찾아보자
- $q$ 번의 입력마다 배열 $a$ 에서 만들 수 있는 최대 mex값을 만들기 위해 최대한 수는 0부터 1, 2, 3 차례대로 만들 수 있게 해야 한다.
- 또한 배열 $a$ 에 있는 수에 $x$ 를 더하거나 뺴거나를 마음껏 쓸 수 있다.
- 즉 배열에 있는 수를 가장 작게 만들다가 가장 작은 값이 있다면 그 다음 작은 값, 또 있다면 그 다음 작은 값으로 설정해주는 게 핵심이다.
$x$ 를 더하거나 빼거나를 맘껏 쓸 수 있다는 것은
- $a_2$ =4, $x$ =3일 때,
- 가능한 $a_2$ 의 값은 1, 4, 7, 10, ... , 300,000,001 ... 무한 개가 있다는 것이다.
배열 $a$ 에 삽입해주는 수는 최댓값은 $10^9$ 로 10억이다.
$a_2$ 의 값이 300,000,001 이라면 $a_2$ 를 1로 만들기 위해 $a_2$ -= 3의 과정을 10억 번 반복해야 한다. 이는 시간 제한안에 해결할 수 없는 연산 횟수이다.
이럴 땐 $a_2$ 의 값인 300,000,001에서 $x$ 를 뺴서 만들 수 있는 가장 작은 값으로 만들기 위해 나머지 연산을 해주어 시간복잡도를 줄일 수 있다.
- $a_2$ = $a_2$ %3 = 300,000,001%3 = 1
문제의 로직을 제대로 만들어 보면,
1) $y$ % $x$ 가 배열에 존재한다면 $y$ %( $x$ *2)를 넣고, $y$ %( $x$ *2)도 존재한다면 $y$ %( $x$ *3), ... ... 이런 식으로 작은 값을 우선으로 배열 $a$ 에 넣어주자.
2) $q$ 의 최댓값은 400,000이다. 매번 $q$ 의 입력마다 mex값을 찾는데 배열 $a$ 의 크기를 탐색한다. 그러면 시간복잡도는 $O$ ( $q$ * $q$ )로 시간제한이 된다.
여기서 시간복잡도를 줄이기 위해 또 방법을 생각해 볼 수 있다.
1)의 과정에서 값을 최대한 작은 것부터 삽임했다. 따라서 mex값은 이전 mex값보다 작아질 수 없다.
$q$ 번의 입력 전에 mex를 0으로 초기화 해두고, $q$ 번의 입력마다 map에서 가장 작은 수를 찾는다면 mex를 찾는 데 총 시간복잡도는 $O(q)$ 로 줄게 된다.
2)의 코드 형태는 대략 아래와 같은 형태이다.

map = {}
mex = 0

for _ in range(q):
	while mex in map:
    	mex += 1

해답코드

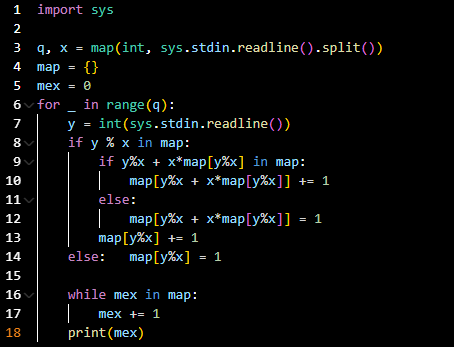
코드라인 1: 파이썬의 int(input())의 경우 입력속도가 느려 시간초과가 발생한다.
		입력속도가 더 빠른 int(sys.stdin.readline())을 사용하기 위해 sys를 import해 주었다.
코드라인 3: q와 x를 입력받는다.
코드라인 4: map 자료구조를 이용한다.
코드라인 5: mex를 0으로 초기화해둔다.
코드라인 6: q번의 입력을 받기 위한 for문이다.
코드라인 7: y를 입력받는다.
코드라인 8, 13: map에 y%x를 key로 하는 값이 있다면 map[y%x] += 1이다.
코드라인 14: map에 y%x를 key로 하는 값이 없다면 map[y%x] = 1이다.
		파이썬에서 맵 자료구조는 key값이 없는데, key값에 접근하려 하면 오류를 일으킨다.
        따라서 key가 없을 때는 value를 1로 설정해준다.
        또한 key값 y%x가 map에 없다는 것은 ai=ai-x (0<=i<배열의 크기) 작업을 통해 만들 수 있는
        가장 작은 값을 map에 넣어준 것이다.
        key값 y%x가 map에 있다면 value를 1 증가시켜 몇 번의 작은 값까지 만들 수 있는지를 나타냈는데,
        이는 코드라인 9~12에서 빠른 시간복잡도로 작업하기 위함이다.
코드라인 9~10: key값 y%x+x*map[y%x]에서 y%x는 만들 수 있는 가장 작은 값이고,
			x*map[y%x]는 차례차례 작은 값을 넣었을 때, 현재 만들 수 있는 작은 값 중 가장 큰 값이다.
            예를 들어, x=2이고, y=2번 입력되어 배열 a=[1, 1]이라고 할 때,
            map[1] = 2가 될것이고, y%x+x*map[y%x]=1+1*map[1] = 3이 된다.
            즉 key값 y%x+x*map[y%x]는 mex값을 최대로 하기 위해 ai=ai-x (0<=i<배열의 크기) 작업을 통해
            현재 만들 수 있는 가장 작은 값 중 가장 큰 값이다.
            key 값 y%x+x*map[y%x]가 map에 있다면, map[y%x+x*map[y%x]] += 1 이다.
코드라인 11~12: key값 y%x+x*map[y%x]가 map 에 없다면, map[y%x+x*map[y%x]]=1 이다.
코드라인 16~17: mex를 -부터 시작해서 map에 key값 mex가 있다면 계속해서 1씩 증가시켜준다.
			이 방법을 통해 mex값을 구하는 데 총 시간복잡도가 O(q)가 된다.
코드라인 17: mex를 출력해준다.