필자가 보는 책(Man Sik Min · Hyeong Chul Jeong · Hyejung Lee, 『CALCULUS』, 한티미디어)에는 The precise definition of a Limit 이 소개되어 있지 않기에, Stewart 선생님의 Calculus 를 보고 그 내용을 정리하려 한다.
0. 주의
필자는 수포자이며, 수학을 전공하지도 않았다. 필자가 공부한 내용을 잊지 않고 환기하기 위해 정리한 글이므로 잘못된, 혹은 더 나아가 틀린 설명이 존재할 수 있다.
따라서 이하의 내용은 어느정도 걸러듣고, 틀린 내용에 대해선 가감없이 댓글 작성 부탁드립니다.
1. Vague statement
필자가 읽는 Calculus 에는 이하와 같이 Limit existence 를 소개한다:
The number is the limit of the function as approaches if, as the values of get arbitrarily close (but not equal) to , the values of approach (or equal) .
여기에서 설명하는 arbitrarily close 는 엄밀한 정의가 아닌, 모호한 설명이므로 이를 수학적으로 풀어서 정의하려 한다.
2. How much closer?
직관적으로 봤을 때, 가 에 가까워지면 역시 5 에 가까워지고, 따라서 가 성립하게 된다는 것을 알 순 있다.
그러나 가 얼마나 에 가까워져야 또한 에 수렴하게 되는지 묻기는 쉽지가 않다.
따라서 와 의 차이에 따른 의 변화를 살펴보려 한다.
- Distance from to
와 의 차가 미만이 되기 위해선, 가 얼마나 과 가까워야 하는가?
먼저, 와 의 차는 이고, 와 사이의 거리는 로 표현할 수 있다. 따라서 위 문제는 아래와 같은 부등식의 형태로 표현할 수 있다:
if but
그러므로 최상단의 문제는 위 의 값을 찾으라는 것과 동일하다. 또한 일때 이므로, 다시 아래와 같이 쓸 수 있다:
if
다시 식을 전개해서 부등식을 풀면 아래와 같다:
따라서 의 값은 임을 알 수 있다. 이러한 방식으로 을 , 로 바꾸어서 다음과 같이 를 구할 수 있다:
if
if
3. The Precise Definition of a Limit
위에서 소개한 , , 그리고 정도의 오차는 허용 가능 범위라 생각할 수 있지만, 이 역시 엄밀한 정의는 아니다.
따라서 가 에 근사함에 따라 가 의 엄밀한 극한이 된다는 것을 증명하기 위해선, 위에서 소개한 각각의 세 숫자 뿐만 아니라 그 어떠한 양수에 대해서도 위 부등식이 일관성 있게 성립해야 한다.
만일 임의의 양수를 로 쓰면 아래와 같이 표현 가능하다:
if
위 수식은 가 에 가까워질 때 역시 에 근사한다는 것을 표현하는 엄밀한 방법이다. 왜냐하면...
- 맨 처음 변수로 놓았던 는 어떠한 양수일 수 있다고 했고
- 와 사이의 거리인 에 대한 와 사이의 거리를 으로 제한(그러나 ) 했기 때문이다.
또한 위 부등식을 풀어서 아래와 같이 쓸 수 있다:
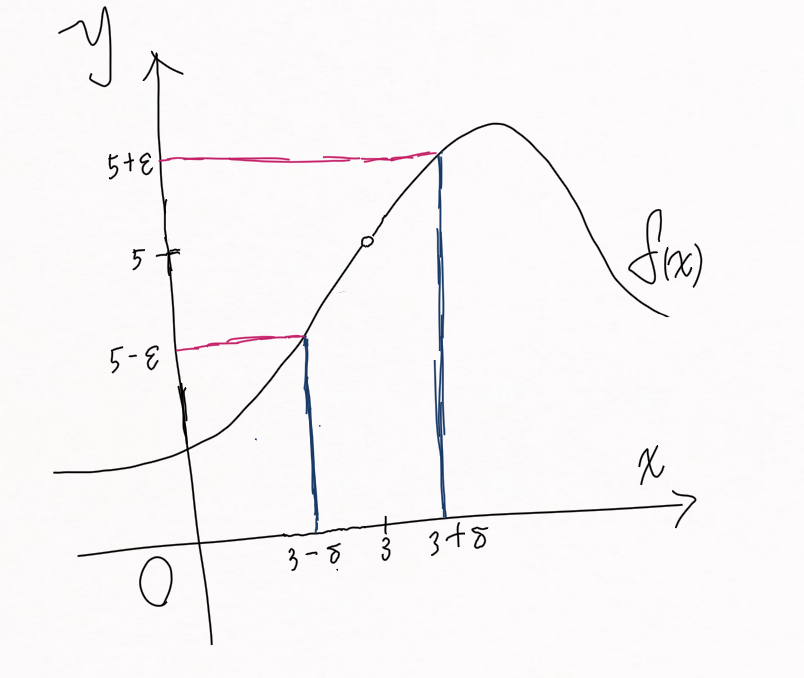
if then
직접 그린 그림이라 개판이긴 하지만 위 수식을 설명하는데에는 아무런 지장이 없으리라 생각한다.
위 내용을 정리해서 # 1. Vague Statement 에서 소개한 극한의 엄밀한 정의가 가능해진다. 아래는 Stewart 선생님의 Calculus 에서 소개한 정의이다:
- Precise Definition of a Limit
Let be a function defined on some open interval that contains the number , expected possibly at itself. Then we say that the limit of as approaches is . and we write...
if for every number there is a number such that
then
출처 (Reference)
[책] Stewart, James. Calculus: Early Transcentals, 9th Ed, p105-106.
[책] Man Sik Min · Hyeong Chul Jeong · Hyejung Lee, 『CALCULUS』, 한티미디어, p50.
