1. Limit Existence

 The number $L$ is the limit of the function $f(x)$ as $x$ approaches $c$ if, as the values of $x$ get arbitrarily close (but not equal) to $c$, the values of $f(x)$ approach (or equal) $L$. We write...

$\lim_{x \to c}f(x) = L$

 In order for $\lim_{x \to c}f(x)$ to exist, the values of $f$ must tend to the same number $L$ as $x$ approaches $c$ from either the left or the right. We write...

$\lim_{x \to c^-}f(x)$

 for the left-hand limit of $f$ at $c$ (as $x$ approaches $c$ through values less than $c$), and

$\lim_{x \to c^+}f(x)$

 for the right-hand limit of $f$ at $c$ (as $x$ approaches $c$ through values greater than $c$).

- Limit Laws

If $L$, $M$, $c$ and $k$ are real numbers and $\lim_{x \to c}f(x) = L$ and $\lim_{x \to c}g(x) = M$, then....

• Sum Rule: $\lim_{x \to c}(f(x) + g(x)) = L + M$
• Difference Rule: $\lim_{x \to c}(f(x) - g(x)) = L - M$
• Constant Multiple Rule: $\lim_{x \to c }(k \cdot f(x)) = k \cdot L$
• Product Rule: $\lim_{x \to c}(f(x) \cdot g(x)) = L \cdot M$
• Quotient Rule: $\lim_{x \to c}\frac{f(x)}{g(x)} = \frac{L}{M}$
• Power Rule: $\lim_{x \to c}[f(x)]^n = L^n$, $n$ a positive integer
• Root Rule: $\lim_{x \to c}{\sqrt[n]{f(x)}} = \sqrt[n]{L} = L^\frac{1}{n}$, $n$ a positive integer
  (If $n$ is even, we assume that $\lim_{x \to c}f(x) = L > 0$)

- Indeterminate form of type $\frac{0}{0}$

• Rational Expressions:
   Step 1. Factor the numerator and denominator.
   Step 2. Cancel the common factor.
• Radical Expressions:
   Step 1. Multiply the numerator and denominator by the conjugate.
   Step 2. Cancel the common factor.

- Definition of Absolute Value

$|x| = \begin{cases} x & \text{if} & x \geq 0 \\ -x & \text{if} & x < 0 \end{cases}$

2. Squeezing Theorem (Sandwich Theorem)

 The Sandwich Theorem Suppose that $g(x) \leq f(x) \leq h(x)$ for all $x$ in some open interval containing $c$, except possibly at $x = c$ itself.

 Suppose also that $\lim_{x \to c}g(x) = \lim_{x \to c}h(x) = L$.

Then...

$\lim_{x \to c}f(x) = L$

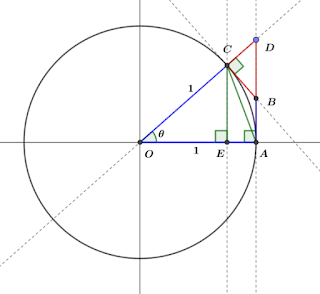
3. Limit of Trigonometric Function

$\lim_{\theta \to 0}\frac{\sin{\theta}}{\theta} = 1$ ($\theta$ in radians)

증명하는 법이 있는데 너무 길어서 생략. 그러나 위 그림만 기억하면 언제든지 증명 가능.

- 오탈자?

• $1 > \frac{\sin{\theta}}{\theta} > \cos{\theta}$ 가 맞는거 아닌가?
• Example 1. Evaluato the following limtis

4. Limit of Exponential and Logarithmic Functions.

- Expoential $e$

$\lim_{x \to \pm \infty}(1 + \frac{1}{x})^x = \lim_{x \to 0}(1 + x)^\frac{1}{x} = 2.7182... = e$

5. Limits Involving Infinity

- Limit of Rational Function in the form $\frac{\infty}{\infty}$.

 Divide both the numerator and the denominator by the highest power of $x$ in theg denominator.

- Horizontal Asymptote

A line $y = b$ is a horizontal asymptote of the graph of a function $y = f(x)$ if either

$\lim_{x \to \infty}f(x) = b$ or $\lim_{x \to -\infty}f(x) = b$.

- Horizontal Asymptote of Rational Functions

$y = \frac{ax^m + .....}{bx^n + ......}$

1. $m = n : y = \frac{a}{b}$ is the horizontal asymptote
2. $m < n : y = 0$ is the horizontal asymptote
3. $m > n :$ there is no horizontal asymptote

- Verticacl Asymptote

  A line $x = a$ is a vertical asymptote of the graph of a function $y = f(x)$ if either...

$lim_{x \to a^+}f(x) = \pm\infty$ or $\lim_{x \to a^-}f(x) = \pm\infty$

6. Continuity

- Continuity Test

 A function $f(x)$ is continous at an interior point $x = c$ of its domain if and only if it meets the following three conditions:

1. $f(c)$ exists      ($c$ lies in the domains of $f$).
2. $lim_{x \to c}f(x)$ exists.  ($f$ has a limit as $x \to c$).
3. $\lim_{x \to c}f(x) = f(c)$. (the limit equals the function value).

7. Average Rate of Change and Instantaneous Rate of Change

 The average rate of change of $y = f(x)$ with respect to $x$ over the interval $[x_1, x_2]$ is...

$\frac{\Delta y}{\Delta x} = \frac{f(x_2) - f(x_1)}{x_2 - x_1} = \frac{f(x_1 + h) - f(x_1)}{h}, h\neq 0$

- Tangent Slope

 The instantaneous rate of change of $f$ with respect to $x$ at $x = a:$ tangent slope

$f'(a) = \frac{dy}{dx}|_{x = a} = \lim_{x \to a}\frac{f(x) - f(a)}{x - a}$ or $\lim_{h \to 0}\frac{f(a + h) - f(a)}{h}$

 The tangent slope is the slope of the line tangent to the curve at a point $x = a$.

8. Intermediate Value Theorem (I.V.T.)

If $f$ is a continous function on a closed interval $[a, b]$, and if $y_0$ is any value between $f(a)$ and $f(b)$, then $f(c) = y_0$ for some $c$ in $[a. b]$.

- 용어 정리

• Rational number: In mathematics, a rational number is a number that can be expressed as the quotient or fraction $\frac{p}{q}$ of two integers, a numerator $p$ and a non-zero denominator $q$.
• Asymptote: In analytic geometry, an asymptote (/ˈæsɪmptoʊt/) of a curve is a line such that the distance between the curve and the line approaches zero as one or both of the x or y coordinates tends to infinity

출처

[책][책] Man Sik Min · Hyeong Chul Jeong · Hyejung Lee, 『CALCULUS』, 한티미디어, p49-82.
[이미지] https://datastory1.blogspot.com/2018/12/blog-post_28.html
[사이트] https://en.wikipedia.org/wiki/Rational_number
[사이트] https://en.wikipedia.org/wiki/Asymptote