2025.04.17 ~ 04.18
Algorithm
Greedy(탐욕 알고리즘)
선택의 순간마다 당장 가장 좋아 보이는 최적의 선택 상황만을 쫓아 최종적인 해답에 도달하는 알고리즘
- 거스름돈, 회의실 배정 등을 구하는 문제가 많다
- Dynamic programming 도 최적의 문제라서 둘 중 어떤 것을 선택할지 생각해보기
수행 방법
- 선택 절차(Selection Procedure) : 현재 상태에서의 최적의 해답을 선택
- 적절성 검사(Feasibility Check) : 선택된 해가 문제의 조건을 만족하는지 검사
- 해답 검사(Solution Check) : 원래의 문제가 해결되었는지 검사하고, 해결되지 않았다면 선택 절차로 돌아가 위의 과정을 반복
Greedy 적용 조건
- 탐욕적 선택 속성(Greedy Choice Property) : 앞의 선택이 이후의 선택에 영향을 주지 않는다. 한번의 선택이 전체 최적해에 영향을 주지 않는다.
- 최적 부분 구조(Optimal Substructure) : 문제에 대한 최종 해결 방법은 부분 문제에 대한 최적 문제 해결 방법으로 구성된다.
배수의 조건이 아닐 때 주의할 점
- 큰 값부터 greedy하게 선택하는 방식은 사용 가능한 단위들이 서로 배수 관계일 때만 항상 최적의 해를 보장(동전 단위)
- 단위들이 배수 관계가 아닐 경우 단순히 가장 큰 단위부터 사용하는 그리디 방식은 잘못된 해를 낼 수 있다
단계 별 최적의 선택 알고리즘
큰 수부터 반복
int count = 0;
while(true) {
<!-- 5키로 봉지로 정확히 나누는 경우 -->
if(n % 5 == 0) {
return n / 5 + count;
} else if (n < 0) { <!-- 3 or 5 조합으로 해결 안되는 상황-->
return -1;
} else if(n == 0) { <!-- 3키로 봉지로만 해결 (없어도 되는 구분) -->
return count;
}
<!-- 5키로로 나누어 떨어지지 않는다면 3키로 봉지 사용 해보기 -->
n = n - 3;
count++;
}동전 개수 최소 알고리즘
큰 수부터 반복
int count = 0; <!-- 필요한 동전의 개수 -->
<!-- 큰 동전부터 사용해볼 수 있도록 배열을 내림차순으로 반복 -->
for(int i = N - 1; i >= 0; i--) {
<!-- 해당 동전을 사용할 가치가 있을 경우, 값보다 동전이 작아진 경우 -->
if(coins[i] <= K) {
<!-- 현재의 동전으로 최대 지불할 수 있는 금액 (동전의 수) -->
count += K / coins[i];
<!-- 지불하고 남은 금액을 다음 동전 확인을 위해 K에 대입 -->
K = K % coins[i];
}
}
return count;심화 - 시작, 끝 시간 고려해서 최대한 많은 시간표 구성 알고리즘
시작시간이 제일 빠른(최소) 것부터 반복
- 시작시간과 끝나는 시간이 같을 수 있는 조건이 주어질 수도 있다.
- 이 경우에는 시작하자마자 끝나는 것으로 생각
<!-- 기본적인 조건은 종료 시간이 빠른 회의 순서로 데이터 정렬 -->
<!-- time 배열 : 각 회의의 [시작시간, 종료 시간] -->
Arrays.sort(time, (t1, t2) -> {
<!-- 종료 시간이 같은 회의가 있다면 시작 시간이 빠른 순서로 정렬 -->
<!-- 경계 시간에 있는 회의가 올바르게 처리 되도록 주는 기준 -->
if(t1[1] == t2[1]) return t1[0] - t2[0];
<!-- 오름차순 정렬 -->
<!--
결과가 음수 → t1이 t2보다 먼저 와야 함
결과가 양수 → t2가 먼저 와야 함
결과가 0 → 두 요소는 같은 순서로 간주
-->
return t1[1] - t2[1];
});
int endTime = 0; <!-- 직전 회의가 끝난 시간을 담아둘 변수 -->
int count = 0; <!-- 회의가 배정 된 개수 -->
<!-- time 배열 안에 있는 회의를 반복하며 회의 시간표에 넣을지 확인 -->
for(int i = 0; i < N; i++) {
<!-- 직전 회의가 끝나는 시간과 일치하거나 그 이후에 시작 되는지 확인 -->
if(time[i][0] >= endTime) {
count++;
endTime = time[i][1]; <!-- 이후 회의 확인을 위해 종료 시간 수정 -->
}
}
return count;DijkstraAlgorithm(다익스트라 알고리즘)
그래프의 한 정점에서 모든 정점까지의 최단거리를 구하는 알고리즘
- 음의 가중치가 존재하면 적용할 수 없다
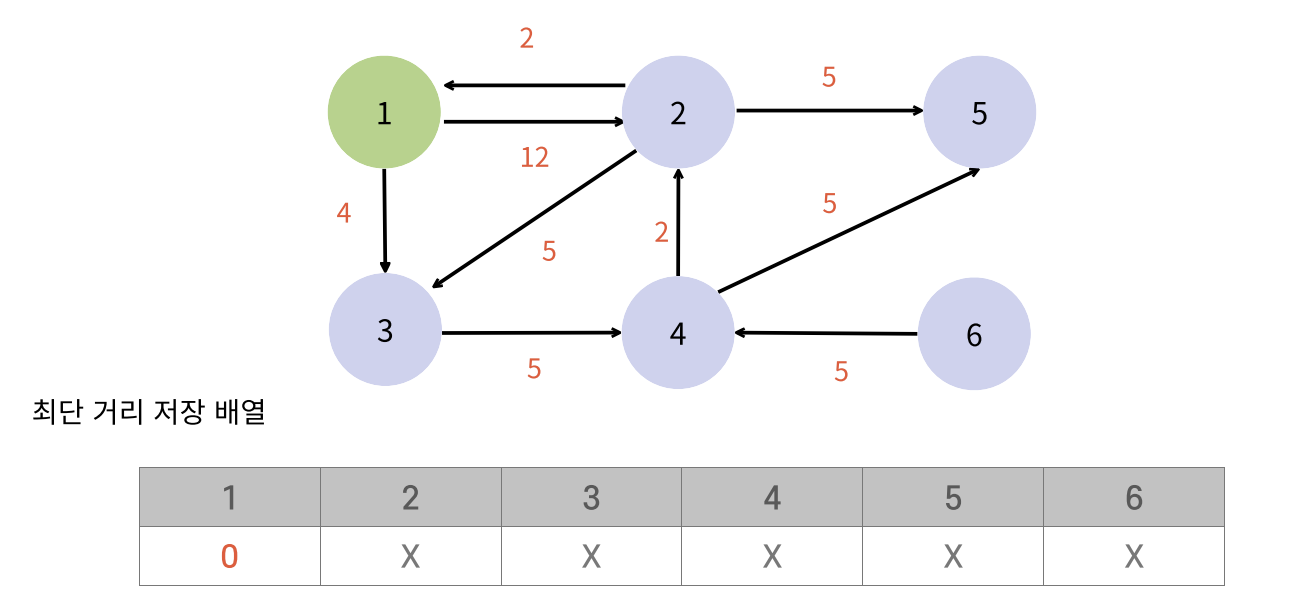
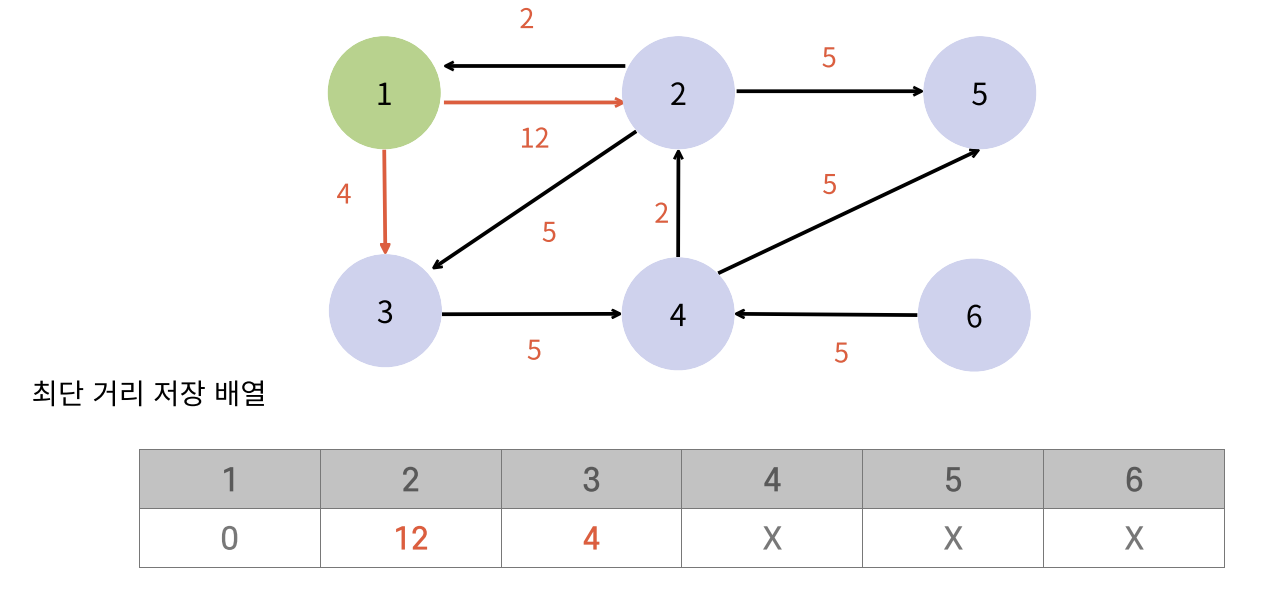
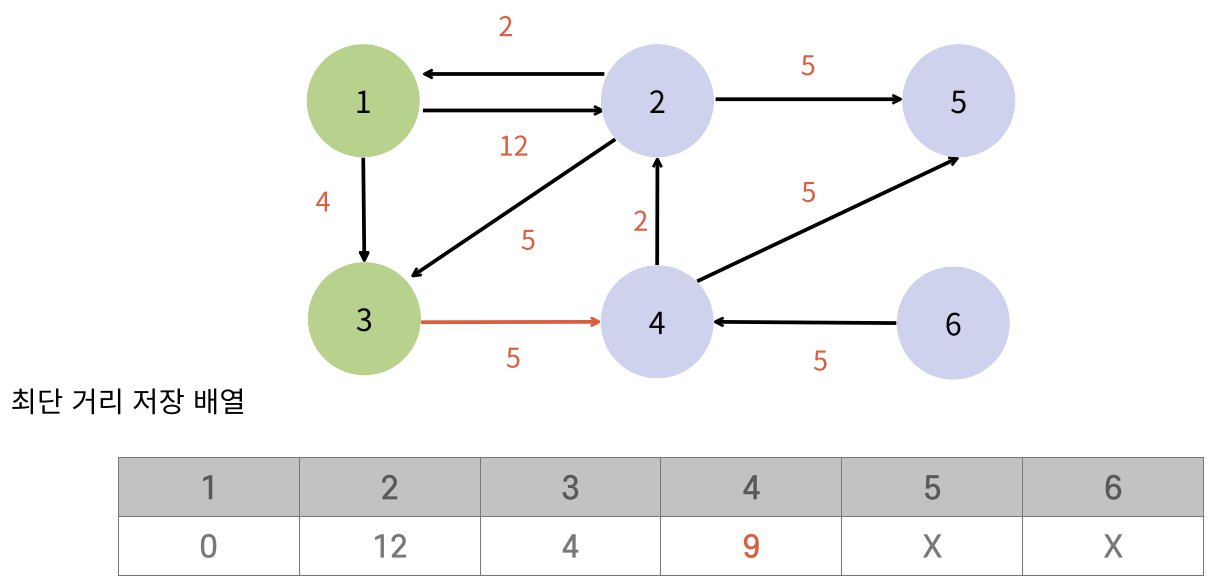
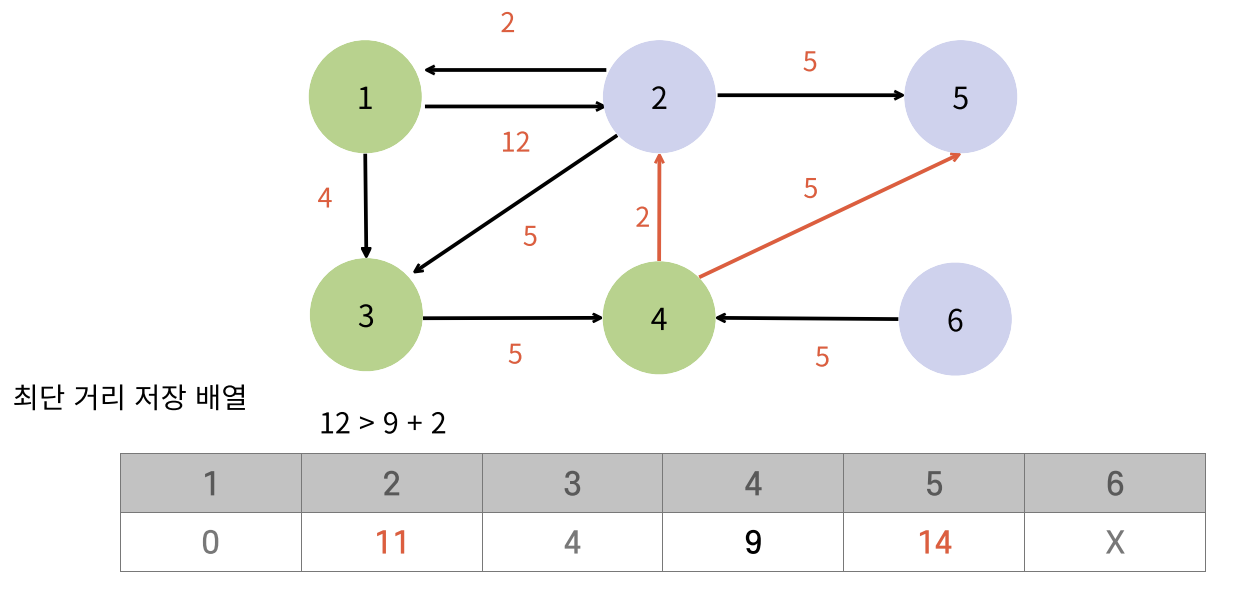
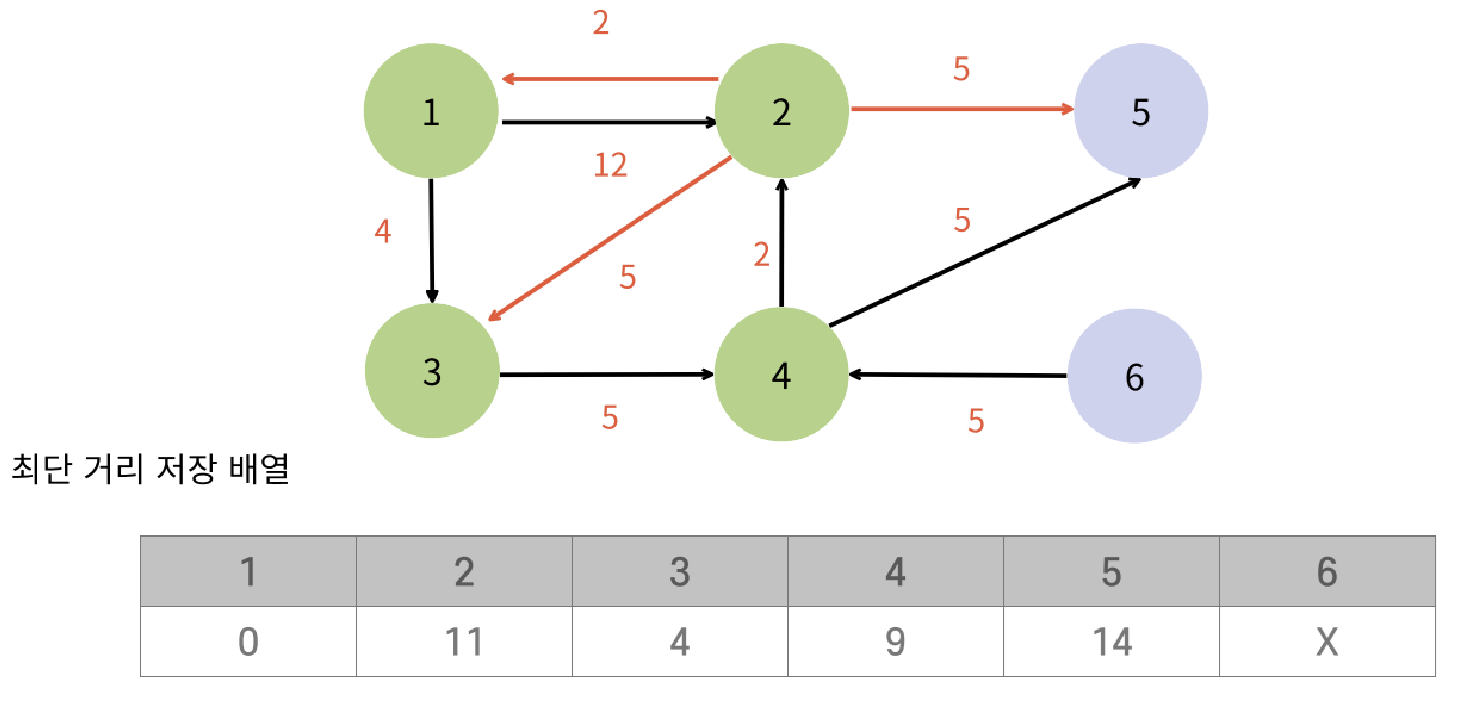
- 다익스트라는 가장 비용이 작은 정점부터 탐색해야 정확한 최단 거리를 구할 수 있기 때문에 우선순위 큐를 많이 쓴다.
- 우선 순위 큐 : 우선순위 큐는 들어온 순서와 상관없이 우선순위가 높은 값(보통 작은 값부터)이 먼저 나간다
static int n, m, start; <!-- 정점 개수, 간선 개수, 시작 정점 -->
static int[] dis; <!-- 다른 노드까지의 거리를 저장할 배열 -->
static class Edge implements Comparable<Edge> {
int ver; <!-- 해당 간선이 연결 된 정점 -->
int cost; <!-- 가중치 -->
Edge(int ver, int cost) {
this.ver = ver;
this.cost = cost;
}
@Override
public int compareTo(Edge o) {
return this.cost - o.cost; <!-- 비용이 낮을수록 우선순위가 높아짐 (오름차순) -->
}
}public static String solution(String input) throws IOException {
BufferedReader br = new BufferedReader(new StringReader(input));
StringTokenizer st = new StringTokenizer(br.readLine());
n = Integer.parseInt(st.nextToken()); <!-- 정점의 개수 -->
m = Integer.parseInt(st.nextToken()); <!-- 간선의 개수 -->
start = Integer.parseInt(st.nextToken()); <!-- 시작할 정점 -->
<!-- 인접 리스트 형태로 그래프 초기화 -->
ArrayList<ArrayList<Edge>> graph = new ArrayList<>();
for (int i = 0; i <= n; i++) {
graph.add(new ArrayList<>());
}
<!-- 각 노드의 가중치 기록할 배열, 0번은 사용하지 않음 -->
dis = new int[n + 1];
<!-- 아직 거리가 판단 되지 않은 경우에는 Integer 최대 값으로 채워 둔다 -->
Arrays.fill(dis, Integer.MAX_VALUE);
for(int i = 0; i < m; i++){
st = new StringTokenizer(br.readLine());
int a = Integer.parseInt(st.nextToken()); <!-- 시작 정점 -->
int b = Integer.parseInt(st.nextToken()); <!-- 도착 정점 -->
int c = Integer.parseInt(st.nextToken()); <!-- 가중치 -->
graph.get(a).add(new Edge(b, c));
}
<!-- 우선순위 큐에 Edge가 담겼을 때 우선 순위는 가중치가 낮은 순서로 정해진다. -->
<!-- 우선순위 큐는 들어온 순서와 상관없이
우선순위가 높은 값(보통 작은 값부터)이 먼저 나간다 -->
<!-- PriorityQueue<Integer> → 기본 타입 int니까 자동으로 오름차순 정렬 -->
<!-- PriorityQueue<Edge> → 사용자 정의 클래스는 어떤 기준으로 정렬해야 할지
compareTo()으로 정렬 기준 선언 -->
PriorityQueue<Edge> pq = new PriorityQueue<>();
pq.offer(new Edge(start, 0));
<!-- 시작 지점은 자기 자신이므로 거리0으로 시작 -->
dis[start] = 0;
while(!pq.isEmpty()) {
Edge tmp = pq.poll();
int now = tmp.ver;
int nowCost = tmp.cost;
<!-- 이미 더 짧은 경로가 있으면 무시 -->
if(nowCost > dis[now]) continue;
<!-- 기준 정점과 연결 된 이웃 정점을 큐에 추가 하는 반복문 -->
for(Edge edge : graph.get(now)) {
<!-- 거리를 기록해두는 배열에 저장 된 값이
현재 비용과 간선을 타고 가는 비용을 더한 값 보다 크다면 -->
<!-- 현재까지 거리 + 간선의 가중치 < 기존 저장 거리 -->
if(dis[edge.ver] > nowCost + edge.cost) {
<!-- 새로운 루트로 업데이트 한다. -->
dis[edge.ver] = nowCost + edge.cost;
<!-- 새로운 경로 추가 -->
pq.offer(new Edge(edge.ver, nowCost + edge.cost));
}
}
}
StringBuilder sb = new StringBuilder();
<!-- 시작 정점이 1번이라 가정하고, 2번 정점부터 출력 -->
for(int i = 2; i < dis.length; i++) {
if(dis[i] != Integer.MAX_VALUE) {
sb.append(dis[i]);
} else {
sb.append("impossible");
}
sb.append(" ");
}
return sb.toString().trim();
}Union & Find
집합 간의 연산을 효율적으로 처리하기 위해 설계 된 데이터 구조
- 집합의 합집합(union)과 특정 원소가 속한 집합의 찾기(find) 연산을 빠르게 처리하는데 유용
- 집합은 서로 다른 원소들로 구성되며, 초기에는 각 원소가 독립적인 집합을 형성
- find(x) : 원소 x가 속한 집합의 대표(root)를 찾는다.
- union(x, y) : x가 속한 집합과 y가 속한 집합을 합친다.
<!-- 부모(root) 노드 저장할 배열 -->
static int[] parent;
<!-- 특정 원소가 속한 집합을 찾는 연산 -->
static int find(int x) {
<!-- 집합의 대표 원소 (루트 노드) 를 찾고
대표 원소를 알면 두 원소가 같은 집합에 속하는지 알 수 있다. -->
if(parent[x] != x) {
parent[x] = find(parent[x]);
}
return parent[x];
}
<!-- 두 개의 집합을 하나로 합치는 연산
두 집합의 대표 원소를 비교하여 두 집합이 연결 되도록 한다. -->
static void union(int x, int y) {
int rootX = find(x);
int rootY = find(y);
// 앞쪽 원소를 root로 하는 기준으로 작성하면
if(rootX != rootY) parent[rootY] = rootX;
}BufferedReader br = new BufferedReader(new StringReader(input));
StringTokenizer st;
<!-- 학생 수와 관계 읽어오기 -->
st = new StringTokenizer(br.readLine());
int N = Integer.parseInt(st.nextToken()); <!-- 학생 수 -->
int M = Integer.parseInt(st.nextToken()); <!-- 제공 된 학생 쌍 -->
<!-- parent 배열 초기화 (처음에는 각각의 요소가 별도의 집합으로 구성) -->
parent = new int[N + 1];
for(int i = 1; i <= N; i++) {
parent[i] = i;
}
<!-- M개의 학생 쌍 처리 -->
for(int i = 0; i < M; i++) {
st = new StringTokenizer(br.readLine());
int a = Integer.parseInt(st.nextToken());
int b = Integer.parseInt(st.nextToken());
union(a, b); <!-- a 학생과 b 학생을 같은 집합으로 만듦 -->
System.out.println("union(" + a + "," + b + ")");
System.out.println("parent : " + Arrays.toString(parent));
}
<!-- 마지막 쌍의 친구 관계 확인 -->
st = new StringTokenizer(br.readLine());
int x = Integer.parseInt(st.nextToken());
int y = Integer.parseInt(st.nextToken());
if(find(x) == find(y)) {
return "YES";
} else {
return "NO";
}KruskalAlgorithm(크루스칼 알고리즘) - 최소 신장 트리(MST: Minimum Spanning Tree)
주어진 그래프의 모든 정점을 연결하는 부분 그래프 중 가중치의 값이 최소인 트리
- 간선의 가중치를 오름차순으로 정렬하고, 사이클을 형성하지 않도록 최소 신장 트리를 구성하는 방법
- union & find 자료구조를 통해 사이클이 생기지 않도록 확인
- 순환은 무시하면서 가중치 계산
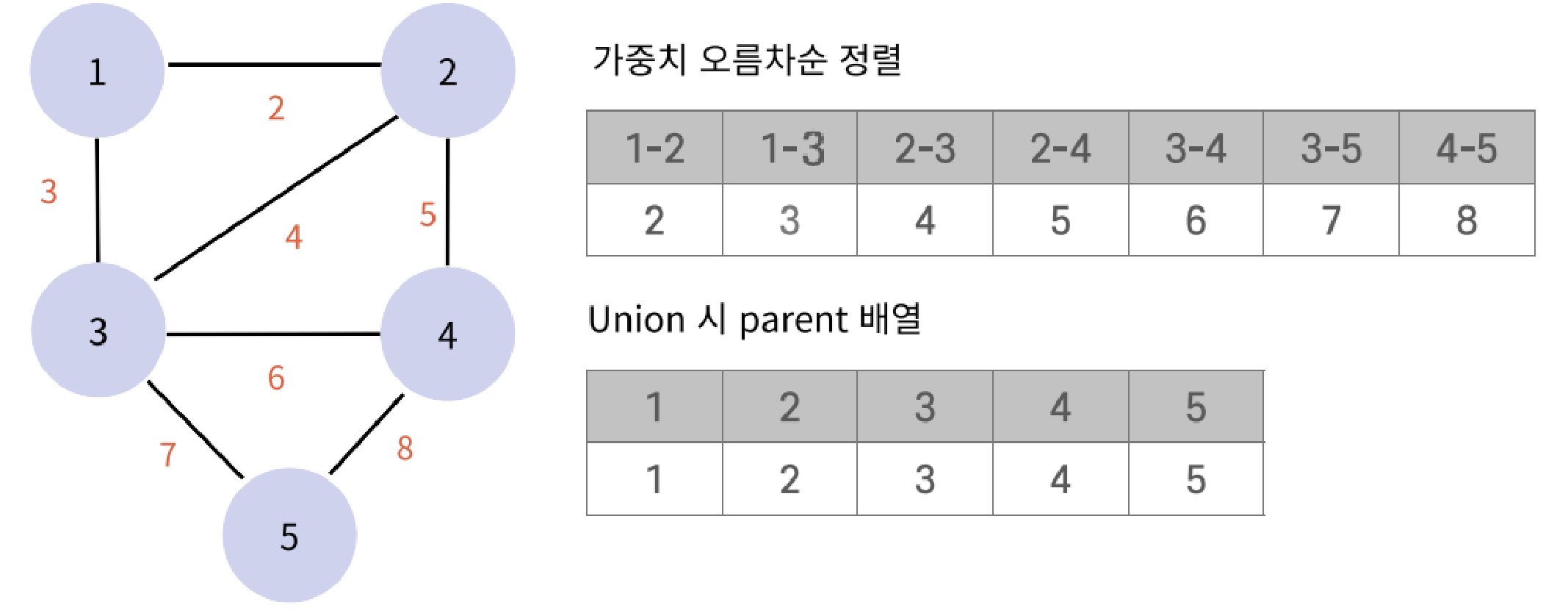
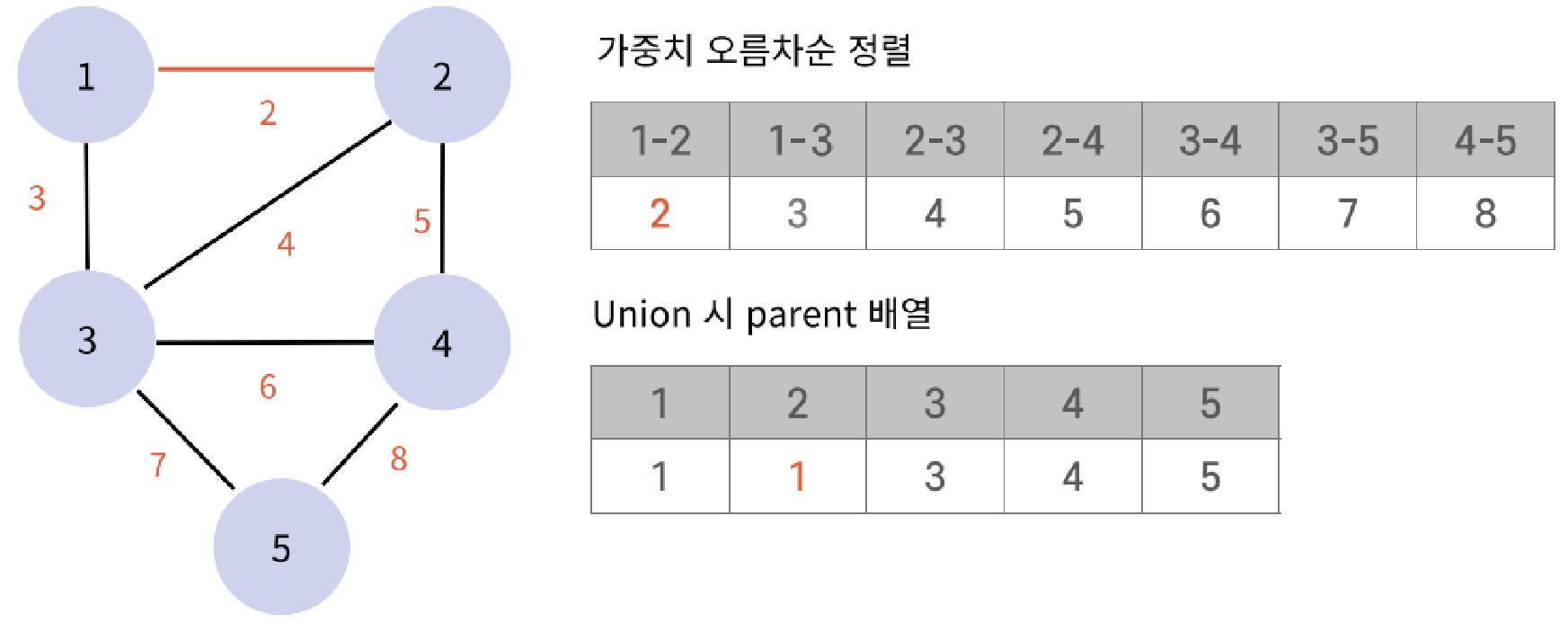
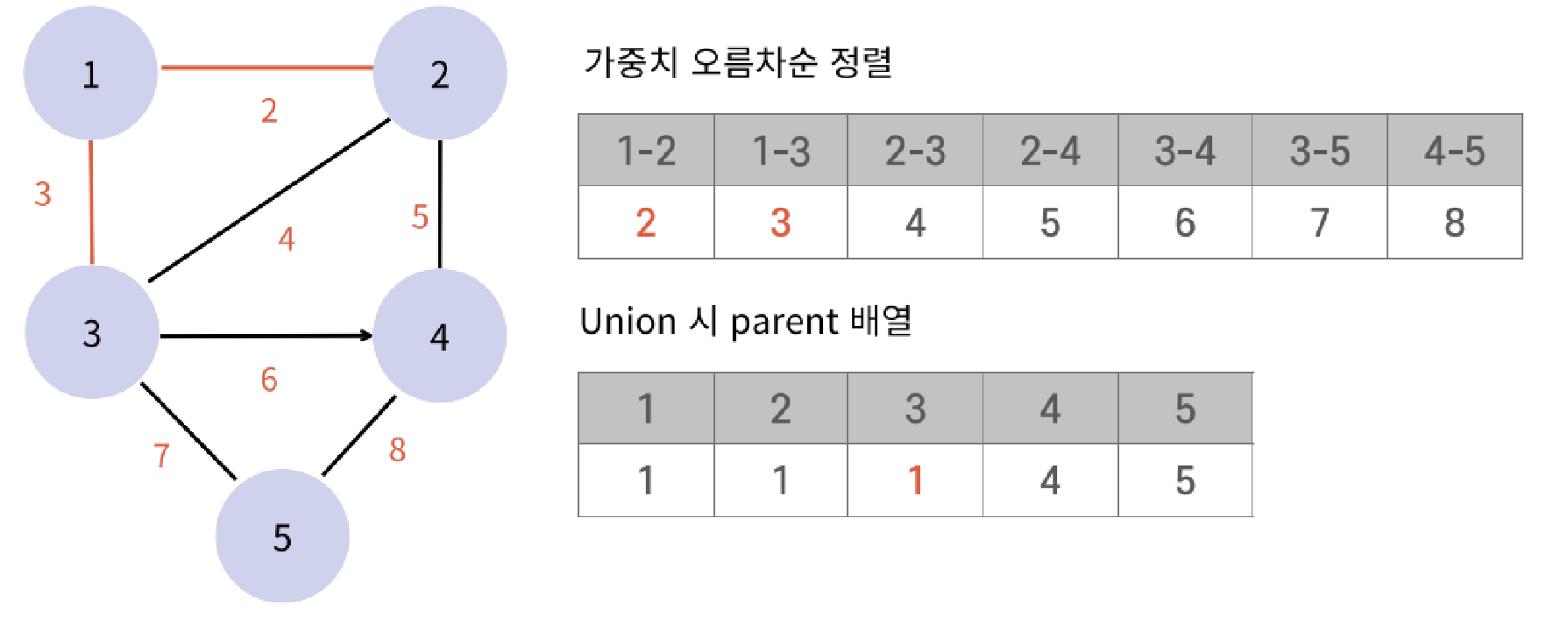
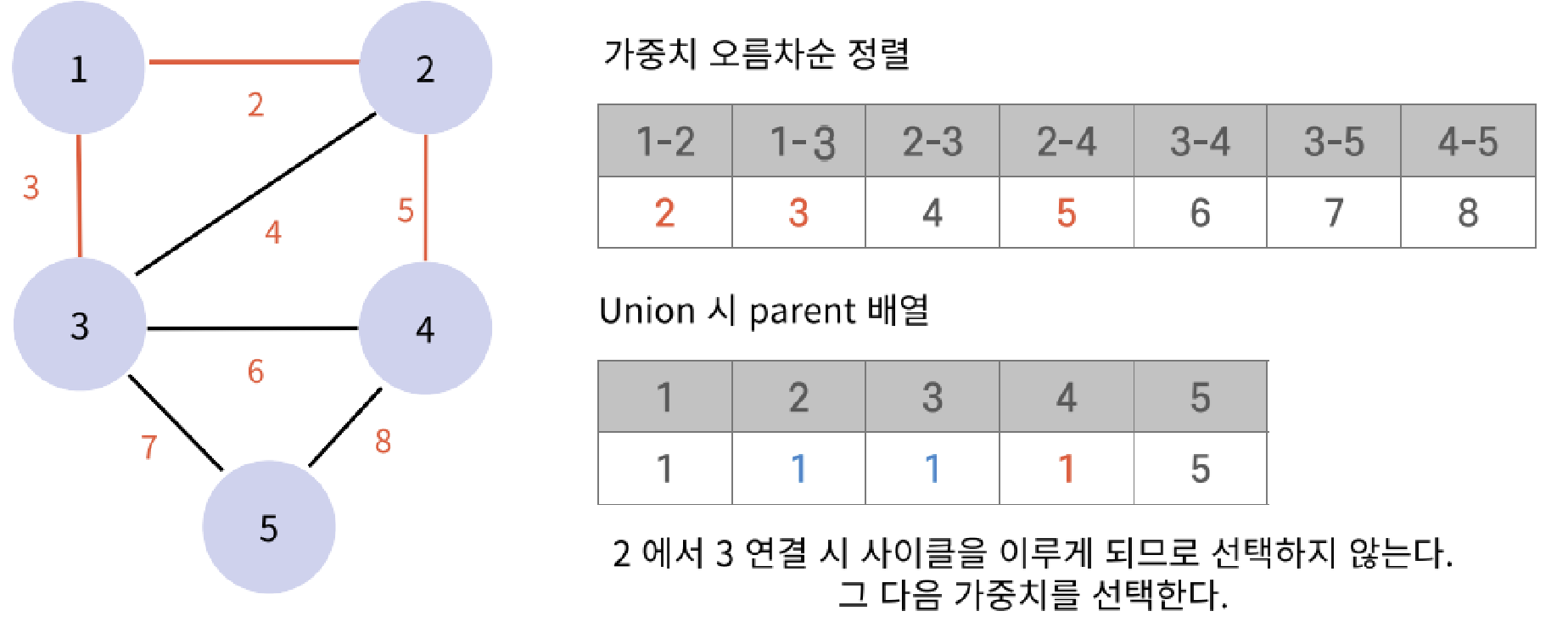
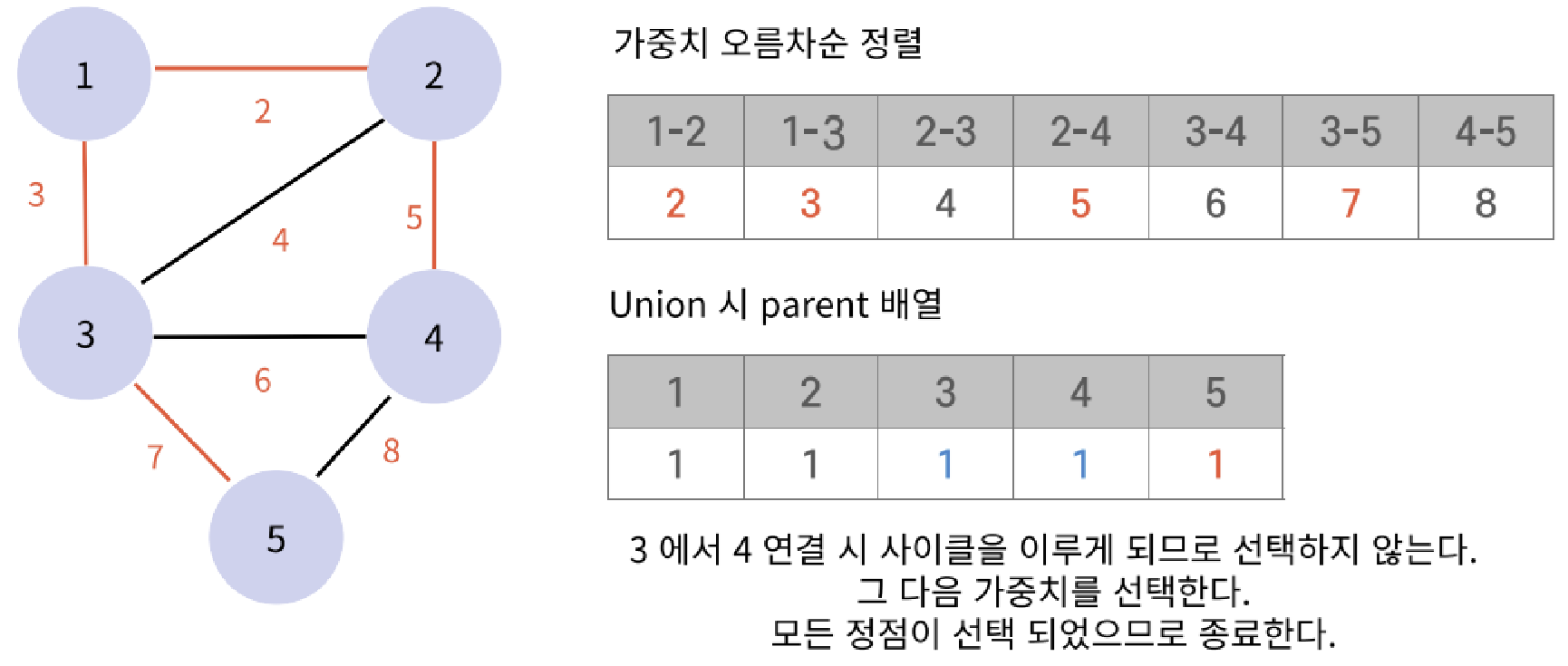
최소 가중치의 합
static int[] parent;
<!-- 간선 정보 클래스 -->
static class Edge implements Comparable<Edge> {
int u, v, weight;
Edge(int u, int v, int weight) {
this.u = u; <!-- 정점 1 -->
this.v = v; <!-- 정점 2 -->
this.weight = weight; <!-- 가중치 -->
}
@Override
public int compareTo(Edge o) { <!-- 간선 정렬 시 가중치 오름차순 적용 -->
return this.weight - o.weight;
}
}
<!-- 특정 원소가 속한 집합을 찾는 연산
이를 통해 집합의 대표 원소(루트 노드)를 찾고, 대표 원소를 알면
두 원소가 같은 집합에 속하는지 확인할 수 있다. -->
static int find(int x) {
if(parent[x] != x) {
parent[x] = find(parent[x]);
}
return parent[x];
}
<!-- 두 개의 집합을 하나로 합치는 연산.
두 집합의 대표 원소를 비교하여 두 집합이 연결 되도록 함. -->
static void union(int x, int y) {
int rootX = find(x);
int rootY = find(y);
<!-- 앞쪽 원소를 root로 하는 기준으로 작성 -->
if(rootX != rootY) {
parent[rootY] = rootX;
}
}BufferedReader br = new BufferedReader(new StringReader(input));
StringTokenizer st = new StringTokenizer(br.readLine());
int V = Integer.parseInt(st.nextToken());
int E = Integer.parseInt(st.nextToken());
Edge[] edges = new Edge[E];
for (int i = 0; i < E; i++) {
st = new StringTokenizer(br.readLine());
int u = Integer.parseInt(st.nextToken());
int v = Integer.parseInt(st.nextToken());
int weight = Integer.parseInt(st.nextToken());
edges[i] = new Edge(u, v, weight);
}
<!-- 유니온 초기화 -->
parent = new int[V + 1];
for(int i = 1; i <= V; i++) {
parent[i] = i;
}
<!-- 1. 가중치 오름차순 정렬 (기준은 내부에 정의 되어 있음) -->
Arrays.sort(edges);
long totalWeight = 0L;
<!-- 2. 가중치 작은 간선부터 선택해나가는 작업 -->
for(Edge edge : edges) {
<!-- 각각의 정점이 연결 되어 있는지 확인 -->
if(find(edge.u) != find(edge.v)) {
<!-- 연결 되어 있지 않다면 정점을 연결 -->
union(edge.u, edge.v);
totalWeight += edge.weight;
}
}
return totalWeight;프림 알고리즘 - 최소 신장 트리
시작 정점에서 시작하여, 최소 가중치 간선을 추가하면서 최소 스패닝 트리를 확장하는 방법
- Priority Queue 방식
- 우선순위 큐를 사용하여 가장 적은 가중치의 간선을 효율적으로 선택
- 방문하지 않은 정점 중, 최소 비용으로 연결 가능한 간선을 우선 선택
static class Edge {
int vertex, weight;
Edge(int vertex, int weight) {
this.vertex = vertex;
this.weight = weight;
}
}BufferedReader br = new BufferedReader(new StringReader(input));
StringTokenizer st = new StringTokenizer(br.readLine());
int V = Integer.parseInt(st.nextToken());
int E = Integer.parseInt(st.nextToken());
<!-- 인접 리스트 그래프 초기화 -->
List<Edge>[] graph = new ArrayList[V + 1];
for (int i = 1; i <= V; i++) {
graph[i] = new ArrayList<>();
}
<!-- 간선 정보 입력 (양방향) -->
for (int i = 0; i < E; i++) {
st = new StringTokenizer(br.readLine());
int u = Integer.parseInt(st.nextToken());
int v = Integer.parseInt(st.nextToken());
int weight = Integer.parseInt(st.nextToken());
graph[u].add(new Edge(v, weight));
graph[v].add(new Edge(u, weight));
}
boolean[] visited = new boolean[V + 1];
<!-- 우선순위 큐: 비용이 낮은 간선이 먼저 나오도록 설정 -->
PriorityQueue<Edge> pq = new PriorityQueue<>(Comparator.comparingInt(e -> e.weight));
<!-- 정점 1에서 시작 -->
pq.add(new Edge(1, 0));
long totalWeight = 0;
while(!pq.isEmpty()) {
Edge edge = pq.poll();
int currentVertex = edge.vertex;
int currentWeight = edge.weight;
if(visited[currentVertex]) continue;
visited[currentVertex] = true;
totalWeight += currentWeight;
<!-- 현재 정점과 연결된 모든 간선을 큐에 추가 -->
for(Edge neighbor : graph[currentVertex]) {
if(!visited[neighbor.vertex]) {
pq.offer(neighbor);
}
}
}
return totalWeight;