[논문 리뷰]Fast and Robust Iterative Closest Point
Fast and Robust Iterative Closest Point
Abstract
- ICP algorithm은 두 점군의 정합하는 중요한 테크닉이다.
- 로보틱스부터 3D reconstruction등 넓은 분야에 적용된다.
- ICP의 가장 큰 문제점은 outlier에 대한 민감성, missing data, partial overlaps등에 의한 느린 수렴.
- Sparse ICP 등의 최근 연구는 sparsity optimization을 통해 계산속도를 희생하고 robustness를 얻음.
- 이 논문에서는 robust하면서 빠르게 수렴하는 방법을 제시함.
- 첫번째로 classical point-to-point ICP 알고리즘이 majorization-minimization(MM) 알고리즘으로 처리될 수 있음을 보일 것.
- 그리고 빠른 수렴을 위한 Anderson acceleration approach를 소개할 것.
- 추가적으로 Welsch's function에 기반한 robust error metric를 도입할 것. 이것은 앤더슨 가속이 포함된 MM 알고리즘을 사용해서 효율적으로 최적화될것이다.
keywords
Rigid Registration, Robust Estimator, Fixed-point iterations, Majorlazer Minimization method, Anderson Acceleration
1. Introduction
Rigid registration : source point set과 target point set을 정합하는 최적의 rigid transformation을 찾는 것.
ICP
- rigid registration에 사용되는 고전적인 방법.
- closest point query in the target set / minimization of distance between corresponding points. ICP는 앞의 두 step을 반복하며 local optimal alignment로 수렴이 보장된다.
- linear convergence rate를 가지기 때문에 수렴속도가 느리다.
- noises, outliers and partial overlaps등의 영향으로 인해 불완전해지는 문제가 있음.
Anderson acceleration
- 컴퓨터그래픽스 분야의 다양한 최적화 문제에 효과적이라고 입증된 numerical technique.
- 과거 m회 iteration을 이용해서 계산을 가속화.
- 기존 ICP의 squared distance metric 대신 새로운 metric 도입.
- Euler angle 대신 Lie algebra 사용.
3. Classical ICP Revisited
-
두 점군 , in 가 주어짐.
-
P와 Q를 align하기위해 rotation matrix 와 translation 를 최적화한다.
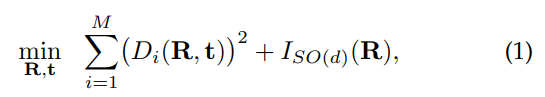
where : transform된 와 target set 사이의 거리.
: 이 SO(d)에 속하면 0, 이외에는 를 return하는 indicator function.
ICP algorithm은 Correspondence step과 Alignment step을 반복하며 수렴한다.
Correspondence step
각 점 마다 가장 가까운 점 를 찾는다. 이 때 distance는 p점이 현재 에 의해 변환된 점과 q점 사이의 거리를 이용한다.
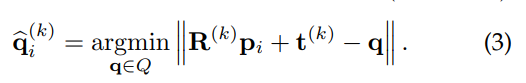
Alignment step
corresponding points 사이의 l2 distance를 최소화하도록 transformation update

Alignment step의 경우 SVD를 이용해 closed form solution을 구할 수 있다.
찾아볼 것 : Least-Squares Rigid Motion Using SVD, MM algorithm