(JS 알고리즘) 동적 프로그래밍

동적 프로그래밍

• 큰 문제를 한 번에 해결하기 힘들 때 작은 문제로 나누어 푸는데, 이 때 이전에 계산한 값을 저장해두었다가 다시 사용한다.
• 큰 문제를 작은 문제로 분할하여 푼다는 점에서 분할정복 알고리즘(ex)합병정렬)과 유사하지만, 한 번 계산했던 값은 저장한다는 점에서 (Memoization, 메모이제이션) 분할정복 알고리즘과 다르다.

사용하기 위해 확인해야 할 두가지

1. 반복되는 하위 문제
2. 최적 부문 구조 : 하위 구조의 최적 해답을 통해 더 큰 범주의 최적 해답을 구성할 수 있다,

파보나치 수열

• 수학에서 피보나치 수(영어: Fibonacci numbers)는 첫째 및 둘째 항이 1이며 그 뒤의 모든 항은 바로 앞 두 항의 합인 수열이다.
  

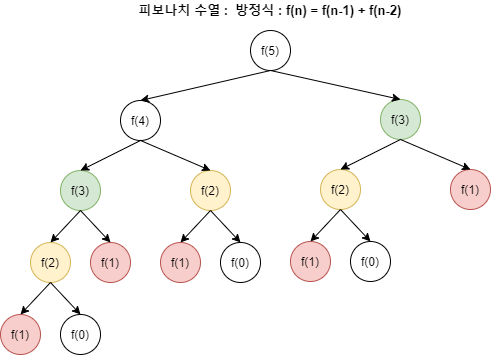
피보나치 수열을 예를 들어보자면, 점화식은 F(n) = F(n-1) + F(n-2)가 된다.

이는 간단하게 재귀함수만으로 구현할 수 있지만, 비교적 그렇게 어마어마하게 크지 않은 수인 50만 생각해보더라도 50을 구하기 위해서 불필요한 재귀가 일어나게 되어 엄청나게 많은 연산이 요구된다.

위의 그림에서도 알 수 있듯이 5를 구하기 위해서 다른 것들이 중복해서 계속 재귀적으로 호출되고 있다.

따라서 다이나믹 프로그래밍을 사용하여 이미 구한 값은 메모이제이션으로 저장을 해놓아서 불필요한 연산 횟수를 줄이면 성능이 매우 좋아진다. 그렇게 되면 시간복잡도가 O(n)으로 해결이 가능해진다.

재귀

• 똑같은 함수 계산을 매번 새로 반복하기 때문에 O(2^n) 시간복잡도를 가진다. (O(n^2)보다 느린 시간복잡도)

function fib(n){  //재귀형 O(2^n)
    if(n === 1) return 1;
    if(n === 2) return 1;
    return fib(n-1) + fib(n-2);
}

개선법 1 : 메모이제이션(Memoization)

• 들어온 값을 메모해두고 똑같은게 다시 들어오면 확인을 통해 다시 실행하는게 아닌 값을 가져다 쓴다.
• 시간복잡도 O(n)

function fib(n,memo=[]){
    if(memo[n] !== undefined) return memo[n]; //있으면 가져다쓰겠다
    if(n<=2) return 1;
    var res = fib(n-1,memo) + fib(n-2,memo);
    memo[n] = res;
    return res;
}

타뷸레이션 : 상향식 접근(Bottom - Up)

• 상향식 방법으로, 작은 문제들부터 답을 구해가며 전체 문제의 답을 찾는 방식 (반복문을 가지고 푼다)
• 호출스택에서의 공간복잡도 제약이 줄어든다.
• 시간복잡도 O(n)

function fib(n){
    if(n<=2) return 1;
    let fibNums = [0,1,1];
    for(let i=3; i<=n; i++){
        fibNums[i] = fib(i-1) + fib(i-2);
    }
    return fibNums[n];
}