(JS 알고리즘)정렬 알고리즘_빠른

Merge Sort(합병 정렬)

• 버블정렬, 선택정렬, 삽입정렬은 확장성이 좋지 않다. 예를 들어 큰 규모의 데이터 정렬에서는 시간이 매우 많이 걸린다.
• 큰 규모의 데이터를 빨리 정렬하기 위해서 합병정렬, 퀵정렬, 기수정렬 등의 알고리즘을 사용할 수 있다.
  • 시간복잡도 O(n^2) -> O(n)

병합정렬 원리

• 병합과 정렬을 조합한 알고리즘이다.
• 요소가 0개 또는 1개의 요소로만 구성된 더 작은 요소로 분할한 다음, 새로 정렬된 배열을 만든다.
• 배열을 0개 또는 1개의 배열로만 구성될 때까지 쪼갠다음, 그 작은 배열들을 합치며 정렬하는 과정을 거친다.
  • 배열이 한개이면 정렬된 것이나 마찬가지이다.
    

병합정렬 헬퍼 함수

function merge(arr1,arr2){ //정렬하는코드
    var results = [];
    let i = 0;
    let j = 0;

    while(i < arr1.length && j < arr2.length){
        if(arr1[i] < arr2[j]){
            results.push(arr1[i]);
            i++;
        }else{   //같은값이어도 arr2로서 실행됨
            results.push(arr2[j]);
            j++;
        }
    }

    while(i<arr1.length){ //위에 루프가 끝났는데 배열 1이나 배열 2에 요소가 남았을때 전부 푸쉬하는거
        results.push(arr1[i]);
        i++;
    }

    while(j<arr2.length){
        results.push(arr2[j]);
        j++;
    }
    return results;
}

병합정렬 의사코드

• 재귀형 코드이다.

  • 비어 있거나 하나의 요소만 있는 배열이 될 때까지 배열을 반으로 나눈다. (slice 사용, 재귀).
  • 아까 작게 나눈 배열들을 원본 배열의 길이로 돌아올 때까지 서로 병합한다. (정렬된 배열을 합치는 헬퍼 함수 활용).
  • 배열이 모두 병합되면 병합된 배열을 반환한다.

병합정렬 코드

function mergeSort(arr){  //분할 후 정렬하기위해
    if(arr.length <= 1) return arr; //arr 길이가 0,1이 될때까지 분할
    let midpoint = Math.floor(arr.length / 2);
    let left = mergeSort(arr.slice(0,midpoint));
    let right = mergeSort(arr.slice(midpoint));
    return merge(left,right);
}

병합정렬 빅오복잡도

• 시간 복잡도(Best case, worst case, average case 모두) : O(nlogn)

  • log n : n개의 요소를 지닌 배열을 1개 이하의 요소만 지닌 배열들로 나누기 위해서는 log2 n 번의 과정이 필요하다. (ex 8개 요소를 지닌 배열을 1개 요소만 지닌 배열들로 나누려면, 8→4→2→1처럼 log2 8(=3) 번의 과정 필요) - 재귀
    n : 최소단위로 나눈 배열들을 다시 합칠 때는 n 번의 비교를 해야한다. (위에서 merge함수)

  • 위 작업들이 함께 연달아 수행되므로, O(nlogn) 의 시간 복잡도를 가지게 된다.

  • 병합 정렬은 어떤 데이터에서도 적용 가능하면서 가장 빠른 편인 정렬 알고리즘이다.

• 공간복잡도 : O(n)

  • 병합 정렬의 공간 복잡도는 O(n)인데, 이는 배열이 커질수록 메모리에 저장해야 하는 배열의 개수가 많아짐을 뜻한다. (참고로 버블정렬의 공간복잡도는 상수였다.) 병합 정렬은 버블 정렬 등 앞에서 살펴본 다른 정렬 알고리즘에 비하면 더 많은 공간을 점유한다.

퀵 정렬

• 퀵 정렬은 재귀를 사용해서 데이터를 쪼개고, 배열이 0개나 1개의 요소를 가지면 정렬된 배열이 된다는 점을 이용해서 정렬을 했던 병합정렬과 같은 가정에서 출발한다.
• 피봇 포인트 기준점을 선택하여 해당 숫자보다 작은 숫자는 모두 왼쪽으로, 큰 숫자들은 오른쪽으로 옮긴다. 이 때 왼쪽과 오른쪽 숫자의 순서는 상관없다.

퀵 정렬 원리

1. 리스트 중 피벗을(를) 선정한다.
2. 피벗앞에는 작은 모든 요소들이 오고, 뒤에는 큰 모든 요소들이 오도록 피벗을 기준으로 리스트를 둘로 나눈다.(분할)
3. 분할된 두 개의 작은 리스트에 대해 재귀적으로 이 과정을 반복한다.
   리스트의 크기가 0이나 1이 될 때까지
4. 재귀 호출이 한 번 진행될 때마다 최소한 하나의 요소(피벗)은 위치가 정해지므로, 이 알고리즘은 반드시 끝난다!

피벗 헬퍼 함수

• 병합 정렬을 구현하려면 먼저 피벗의 양쪽에 있는 배열의 요소를 배열하는 기능을 담당하는 함수를 구현하는 것이 유용하다.

• 피벗보다 작은 모든 값을 피벗의 왼쪽으로 이동시키고, 피벗보다 큰 모든 값을 피벗의 오른쪽으로 이동하도록 배열의 요소를 재정렬한다.

• 헬퍼함수는 새 배열을 만들지 않고 기존 배열에 대해서 작업을 한다.

• 완료되면 헬퍼 함수는 피벗의 인덱스를 반환한다.

• 피벗 선택

  • 퀵 정렬의 런타임은 부분적으로 피벗을 선택하는 방법에 따라 다르다.
  • 피벗을 정렬 중인 데이터 세트의 대략 중앙값이 되도록 설정하면 이상적이다.

function pivot(arr,start=0,end=arr.lenght-1){ //재귀적으로 사용할 pivot 헬퍼함수
    var pivotpoint = arr[start]; //맨처음 요소로 피봇포인트 설정
    var swapidx = start;
    
    for(let i=start+1; i<=end; i++){
        if(pivotpoint > arr[i]){
            swapidx++;
            [arr[swapidx],arr[i]] = [arr[i],arr[swapidx]]; //작은걸 추적해가며 스왑해줌
        }
    }
    
    [arr[start],arr[swapidx]] = [arr[swapidx],arr[start]];
    return swapidx;
}

퀵 정렬 코드

function quickSort(arr, left = 0,right = arr.length-1){
    if(left<right){
         let pivotIdx = pivot(arr,left,right); //pivot 함수 실행으로 반환된 인덱스 값
        
        //하나가 구해지고 그것의 왼쪽 정렬
        quickSort(arr,left,pivotIdx-1);
        //하나가 구해지고 그것의 오른쪽 정렬
        quickSort(arr,pivotIdx+1,right);
    }
    return arr;
}

퀵 정렬 빅오

• 시간 복잡도: Best case , average case: O(nlogn)
  퀵정렬도 병합정렬처럼 log2 n 만큼의 decompostion(분할) 작업을 해야 한다. 예를 들어 32개 요소가 있는 경우에는 절반씩 계속 나누어 1개의 요소씩으로 파편화하는데 5번(log2 32)번의 분할을 해야 한다.
  이렇게 매 분할마다 n번의 비교를 해야 한다.

• Worst case : O(n^2)
  만약 이미 정렬이 되어 있는 배열을 퀵정렬하고, 선택된 pivot이 항상 가장 작은 값이라면 (가장 큰 값이거나), 모든 요소에 대해 n번의 분할을 하고 매번 모든 요소에 대해 n번의 비교를 해서, n^2의 시간이 걸린다.

  Tip! pivot으로 지금까지 했던 것처럼 첫 번째 요소를 선택하는 대신에 무작위(또는 가운데)로 요소를 선택하는 방식으로 상기 문제를 피할 수 있다. 이렇게 하면 정렬된 배열이라고 할지라도 문제 발생을 피할 확률을 높일 수 있다.

• 공간 복잡도 : O(logn)

기수정렬

• 비교를 통해 정렬하는게 아닌 기수정렬
• 기수정렬은 대상들을 직접 비교하지 않는다. 그러나 숫자에 대해서만 정렬할 수 있다.
• 숫자의 크기에 대한 정보가 숫자의 자릿수에 이미 저장되 있다는 사실을 이용하여 각 자릿수의 숫자를 나눠 담고, 가장 큰 숫자의 자리 수 까지 이를 반복한다.
  

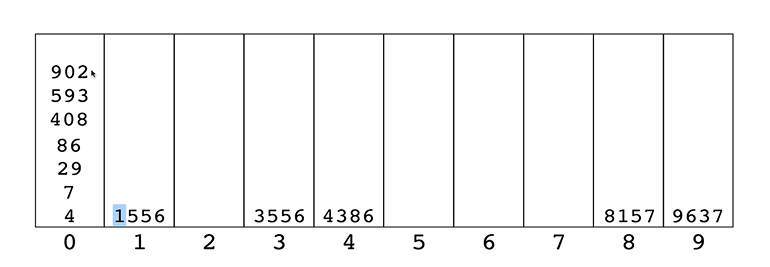
기수정렬 헬퍼함수(자릿수 반환)

• getDigit(num,i) > 숫자 num의 i번째 자릿수 반환

function getDigit(num,i){  //숫자에서 몇번째 자리에 어떤 숫자가 있는지 알아내기
    return Math.floor(Math.abs(num) / Math.pow(10,i)) % 10; 
}

• digitCount(num) > 주어진 숫자의 총 자릿수 알아내기

function digitCount(num){ //주어진 숫자의 총 자릿수 알아내기
    if(num === 0) return 1;
    return Math.abs(num).toString().length;
}

• mostDigits(arr) > 주어진 숫자 배열 중 가장 큰 숫자의 자릿수 반환

function mostDigits(arr){
    let max = 0;
    for(let i=0; i<arr.length; i++){
        if(max < digitCount(arr[i])){
            max = digitCount(arr[i]);
        }
    }
    return max;
}

기수정렬 코드

function 기수정렬(nums){ //radixSort
    var maxdigit = mostDigits(nums); //들어온 입력 중 최대 자릿수 알아내기

    for(let i=0; i<maxdigit; i++){ //최대 자릿수 만큼 반복 (버킷에서의 정렬)
        let digitBucket = Array.from({length : 10},() => []); //하나의 배열안에 10개의 하위배열생성
        for(let j=0; j<nums.length; j++){ //nums배열에서 요소 선택 루프
            let digit = getDigit(nums[j],i);
            digitBucket[digit].push(nums[j]);
        } //여기까지는 버킷에 넣어서 구성은 하지만 배열에 들어간 순서대로 새 배열을 반환해줘야함
        nums = [].concat(...digitBucket);
    }
    return nums;
}

참고 문법

• 빈 배열 여러개 만들기

console.log(Array.from({ length: 10 }, () => []));
// [ [], [], [], [], [], [], [], [], [], [] ]

console.log(Array.from({ length: 10 }, () => ["Hi"]));
// [ [ 'Hi' ], [ 'Hi' ], [ 'Hi' ], [ 'Hi' ] ]

• 배열 안에 요소로 있는 배열들 한 배열로 합치기

console.log([].concat(...[[1], [2], [3]])); // [1, 2, 3]

기수정렬 빅오

n : 정렬할 항목 수, k : 자릿수

• 시간복잡도 : O(nk)
• 공간복잡도 : O(n+k)