(JS 자료구조) 그래프(Graph)

그래프(Graph)

그래프란?

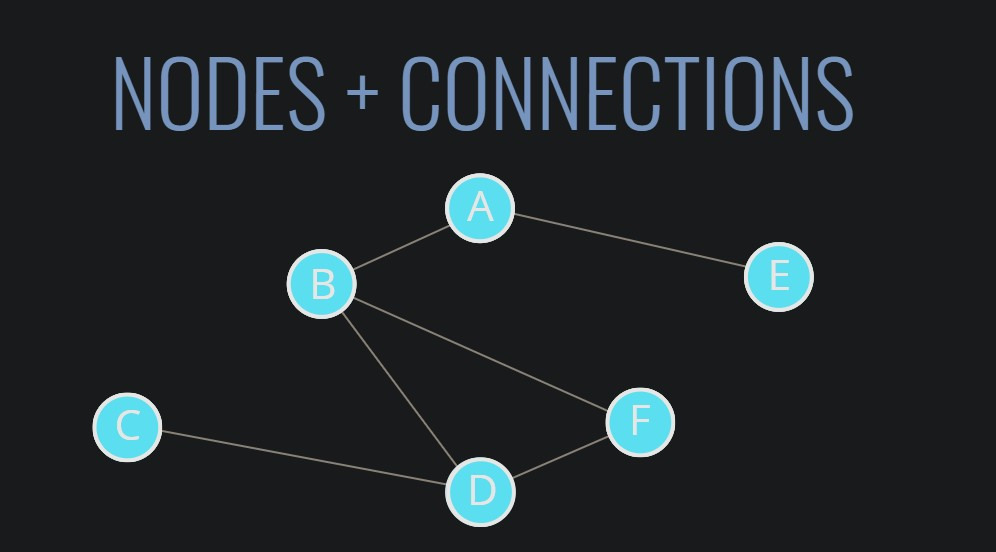
• 그래프는 노드나 노드들의 연결을 모은 것이다.(노드+연결선)
• 그래프는 트리는 포괄하는 개념이다. 트리는 그래프의 일종으로 볼 수 있다.
  • 트리는 그래프의 한 종류지만 한 노드에서 다른 노드로 가는 경로가 하나만 존재
• 그래프를 코딩하는 방법에는 여러가지가 있지만 인접 리스트,인접 행렬을 살펴보고 인접 리스트를 사용하여 그래프를 만들어보자
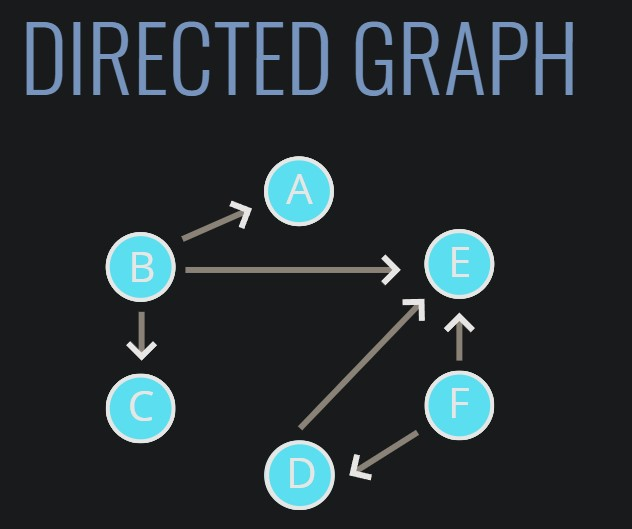
• 그래프는 유한한(가변적인) 꼭지점(노드)들의 집합으로 구성된 데이터 구조다. 이 꼭지점들의 집합에 순서가 없는 경우에는 무방향 그래프(Undirected graph) 이고, 순서가 있는 경우에는 방향 그래프(Directed graph)라고 한다.
  • 무방향 그래프의 예로 페이스북 친구추가, 방향 그래프의 예로 인스타 팔로우(맞팔)등이 있다.
• 아래와 같은 이미지도 유효한 그래프다. 트리와 달리 부모 노드 같은 것은 없다. 그래프에서 노드는 모두 똑같이 취급되며, 단지 서로 다른 방식으로 연결될 뿐이다.
  
• 그래프 활용사례
  • 지도 기능
  • 구글 지도와 방향 안내
  • 위치, 길찾기
  • SNS
• 그래프 관련 용어
  • Vertex(정점) : 노드, 그림의 동그라미들
  • Edge(간선) : 노드 사이의 연결,화살표

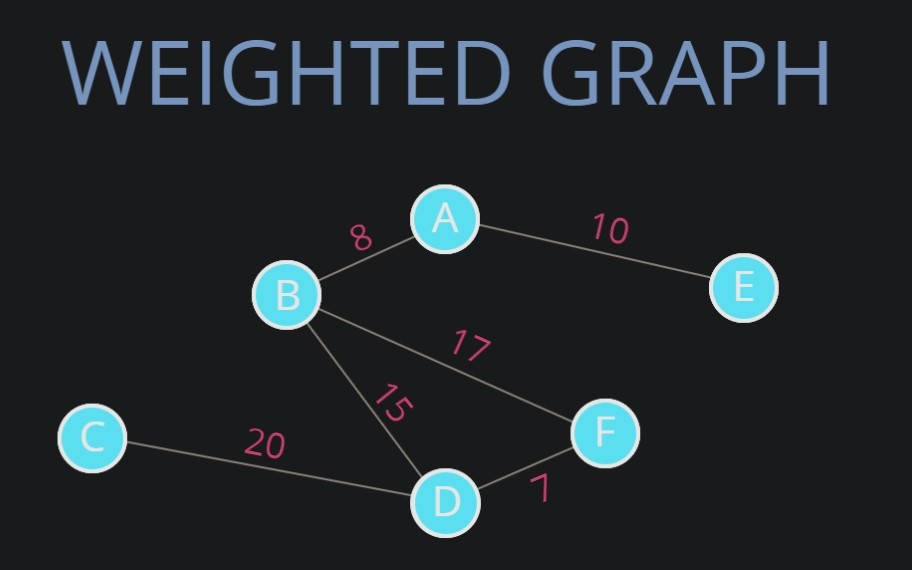
방향/무방향, 가중/비가중 그래프

• 무방향 그래프는 간선에 방향이 없고 양방향 연결이다.(위 그림)

• 방향 그래프는 간선에 정해진 방향(화살표)가 있다.
  

• 가중 그래프는 간선에 값이 부여된 그래프다.

• 비가중 그래프 -> 위 그림들
  

인접 행렬, 인접 리스트

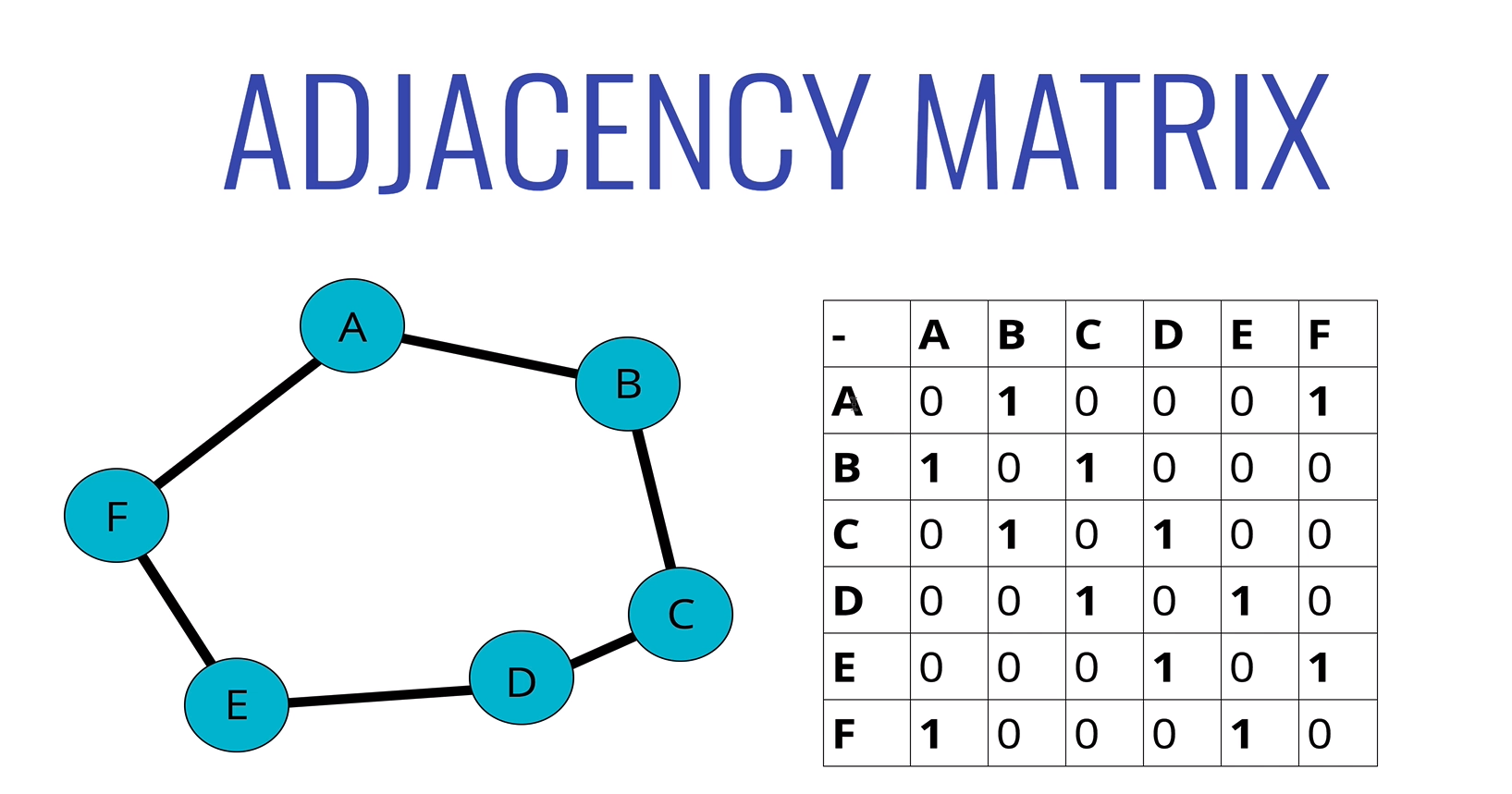
인접 행렬

• 인접 행렬은 2차원 구조로 보통 중첩 행렬로 표현
  • 행과 열에 맞춰 정보를 저장한다.
  • Vertex를 추가할 때마다 행,열에 한줄씩 추가된다.
• 

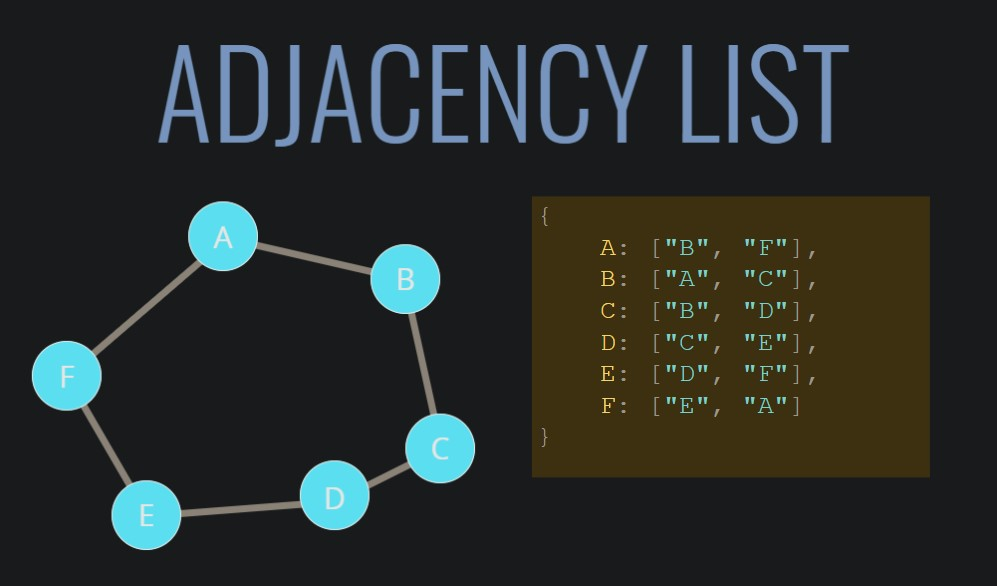
인접 리스트

• 그래프의 노드와 간선 관계를 아래 이미지처럼 해시 테이블을 이용한 인접 리스트로 저장할 수 있다. 만약 아래 예시에서 C노드와 다른 노드들 간 간선을 확인하려면, 인접리스트의 ‘C’ 키에 있는 ['B', 'D'] value를 통해 C 노드는 B노드 및 D노드와 연결되어 있다.
  

인접 행렬, 인접 리스트 빅오

• V : 정점(Vertex)의 갯수, E : 간선(Edge)의 갯수
  
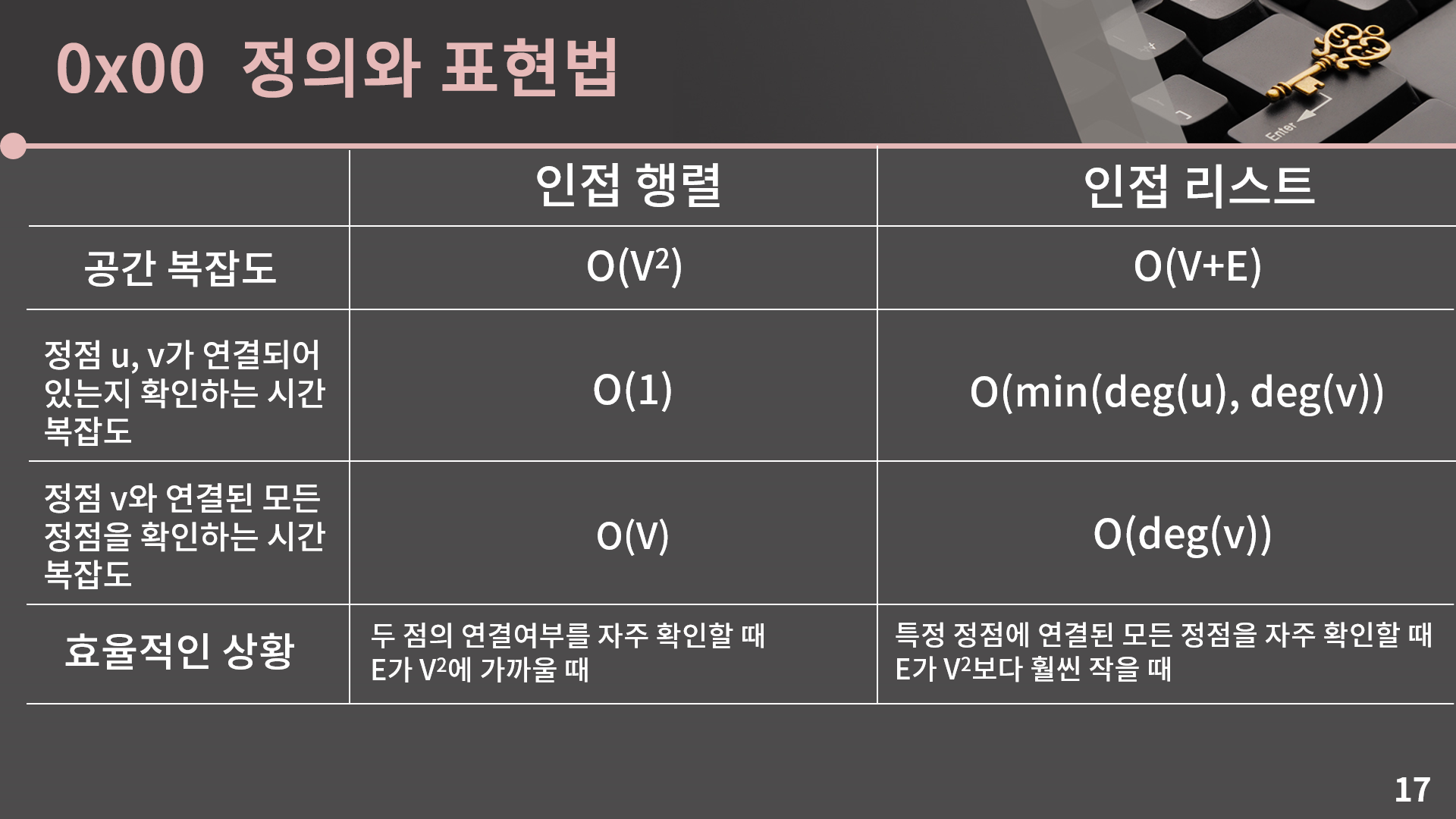
• 인접 행렬은 2차원 구조이기 때문에 O(v^2)의 공간복잡도를 가진다.
• 인접 리스트는 실제 연결만 저장한다.
• 간선이 많지 않고 퍼져있는 그래프에선 인접 리스트를 사용하는게 좋다
  • 인접 행렬보다 더 적은 공간을 차지한다.(간선 순회가 빠름)
  • 인접 행렬은 간선을 확인하기 위해선 모든 간선에 루프를 돌아서 찾아야 한다.(없는 연결도 전부 접근해야함)
  • 인접 리스트에서 특정 간선이 존재하는 것을 확인하는 것은 느려질 수 있다.(O(V+E) -> 행렬에서는 O(1))

인접 리스트 그래프 구현

• 실제로 데이터는 퍼져있는 경우가 많다. 정점의 개수는 아주 많지만 그게 서로 전부 연결이 되어 있지는 않은 경우가 많기 때문에 인접 리스트로 그래프를 구현해보자!

기본 구조

class Graph{
    constructor(){
        this.List = {};
    }
}

정점 추가 메소드(addVertex)

• 정점 추가 메소드는, 입력 받은 정점이 인접리스트에 없으면 인접리스트에 정점 key에 빈 배열을 value로 지정해준다.

addVertex(key){
        if(!this.List[key]) this.List[key] = []; 
    }

간선 추가 메소드(addEdge)

• 간선 추가 메소드는, 추가하려는 간선으로 이어진 두 개의 정점을 입력받고, 이들을 인접리스트에서 서로의 정점의 배열에 push하도록다.

addEdge(vertex1,vertex2){
        this.List[vertex1].push(vertex2);
        this.List[vertex2].push(vertex1);
    }

• 

간선 제거 메서드(removeEdge)

• 간선 제거 메서드는, 제거하려는 간선으로 이어진 두 개의 정점을 입력받고, 인접리스트의 각각 정점들의 value에서 상대 정점만 제외하여 반환(filter 메서드 사용)된 배열을 재할당한다.

removeEdge(vertex1,vertex2){
        this.List[vertex1] = this.List[vertex1].filter((v) => v !== vertex2)
        this.List[vertex2] = this.List[vertex2].filter((v) => v !== vertex1)
    }

• 

정점 제거 메서드(removeVertex)

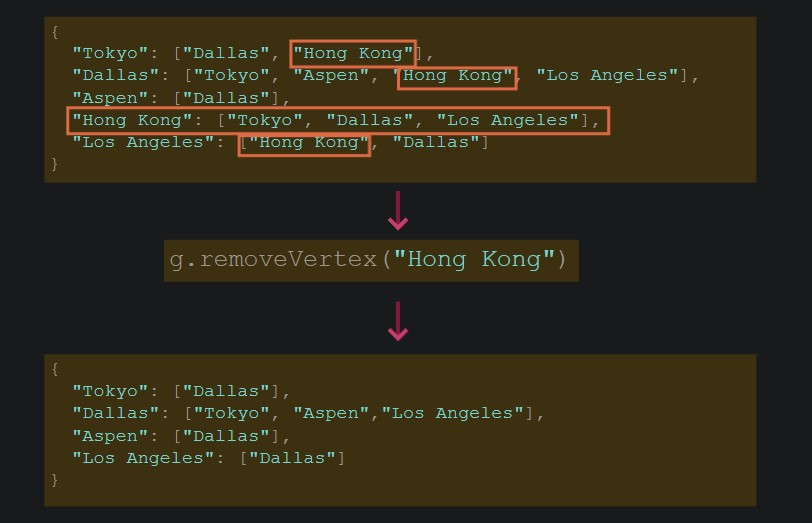
• 정점을 제거하려면, 정점과 연결된 모든 간선들을 제거하고 그 정점도 삭제해야 한다.

removeVertex(vertex){
        this.List[vertex].forEach((v)=> this.removeEdge(vertex,v));
        delete this.List[vertex]; //해당 키값을 아예 삭제
    }

• 

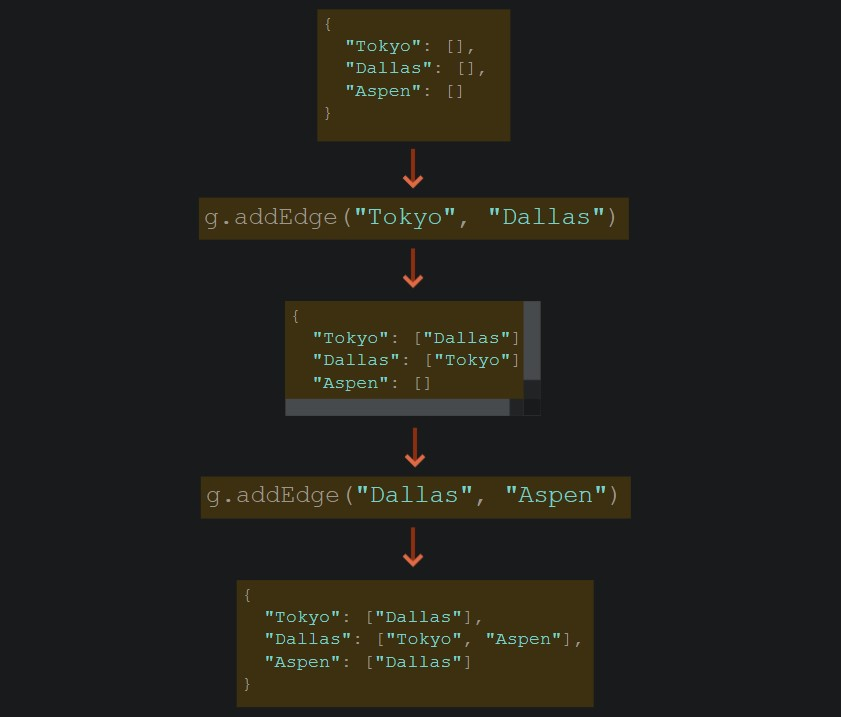
코드 실행 결과

• 해당 클래스의 인스턴스 메서드들을 아래와 같이 실행하면, 주석과 같은 그래프 자료구조가 만들어진다.

const g = new Graph();

g.addVertex("A");
g.addVertex("B");
g.addVertex("C");
g.addVertex("D");
g.addVertex("E");
g.addVertex("F");

g.addEdge("A", "B");
g.addEdge("A", "C");
g.addEdge("B", "D");
g.addEdge("C", "E");
g.addEdge("D", "E");
g.addEdge("D", "F");
g.addEdge("E", "F");

//          A
//        /   \
//       B     C
//       |     |
//       D --- E
//        \   /
//          F