(JS 알고리즘) 트리 순회 - BFS(너비우선탐색), DFS(깊이우선탐색)

트리 순회(Tree traversal)

• 트리의 모든 노드를 순회하는 2가지 방법
  • Breadth-frist Search(BFS, 너비우선탐색)
  • Depth-first Seacrh(DFS, 깊이우선탐색)

기본구조

class Node {
  constructor(value) {
    this.value = value;
    this.left = null;
    this.right = null;
  }
}

class BinarySearchTree {
  constructor() {
    this.root = null;
  }
	// 메서드 생략
}

BFS(너비우선탐색)

• 같은 레벨의 노드들을 우선적으로 탐색(형제요소)
  

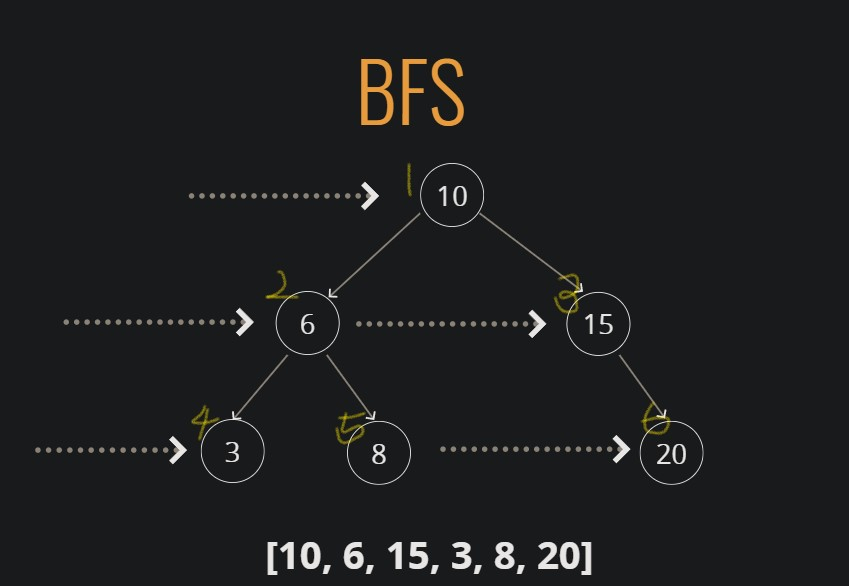
BFS(){
  		//방문 순서대로 저장할 변수와 추적하기 위한 q를 배열로 만듬
        var data = [];
        var q = [];
        var temp = this.root;
        q.push(temp);
        while(q.length){
            temp = q.shift();
            data.push(temp.value);
          	//dequeue된 요소 왼쪽,오른쪽에 값이 있으면 q에 푸쉬
            if(temp.left) q.push(temp.left);
            if(temp.right) q.push(temp.right);
        }
        return data;
    }

깊이우선탐색(DFS)

• 깊이우선탐색의 방향은 트리의 수직 방향이고, 아래로 내려간 다음에 다시 올라온다.
• 깊이우선탐색에는 세 가지 방법이 있다. 모두 재귀를 사용하며, 이 세 가지 방법의 각각의 코드들은 재귀의 헬퍼함수 내에서 data.push(node.value); 한 줄의 위치만 다르고 나머지는 동일한다.
  • PreOrder(전위순회)
  • InOrder(중위순회)
  • PostOrder(후위순회)

PreOrder(DFS) - 전위우선 [루트 - 왼쪽 자식 - 오른쪽 자식]

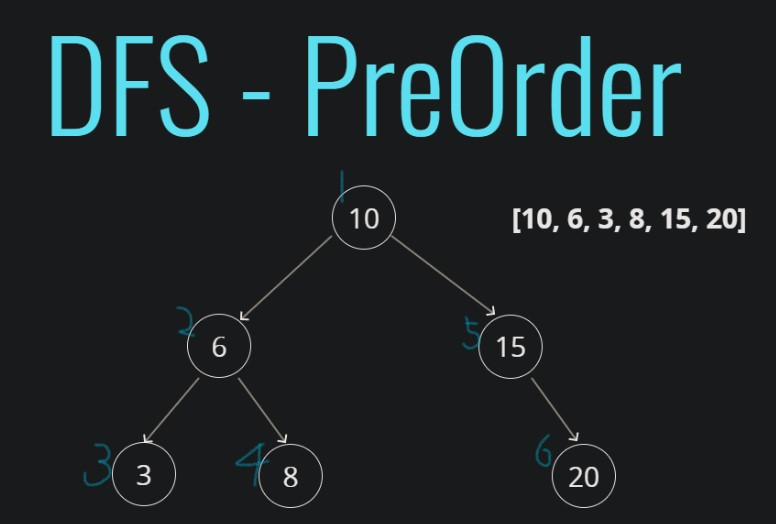
DFSPreOrder(){
        var data = [];
        let temp = this.root;
        function Preorder(node){
            data.push(node.value);
            if(node.left) Preorder(node.left);
            if(node.right) Preorder(node.right);
        }
        Preorder(temp);
        return data;
    }

InOrder(DFS) - 중위우선 [왼쪽 자식 - 루트 - 오른쪽 자식]

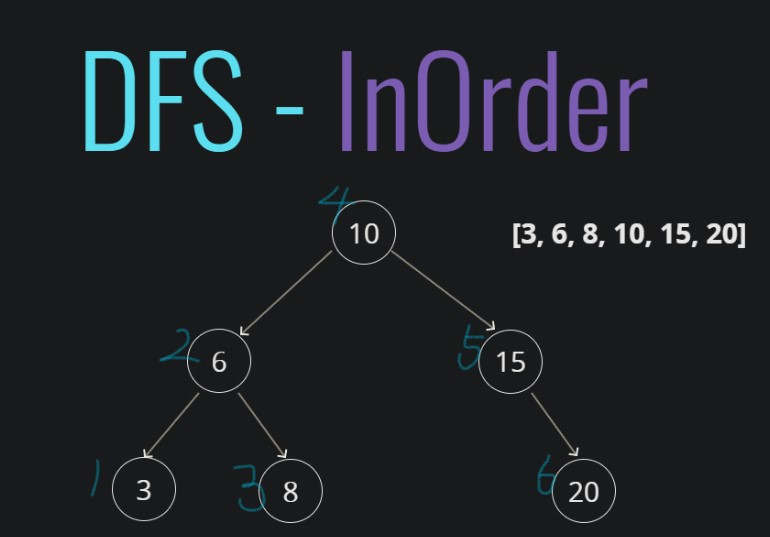
DFSInOrder(){
        var data = [];
        function InOrder(node){
            if(node.left) InOrder(node.left);
            data.push(node.value);
            if(node.right) InOrder(node.right);
        }
        InOrder(this.root);
        return data;
    }

PostOrder(DFS) - 후위우선(가지치기 형식) [왼쪽 자식 - 오른쪽 자식 - 루트]

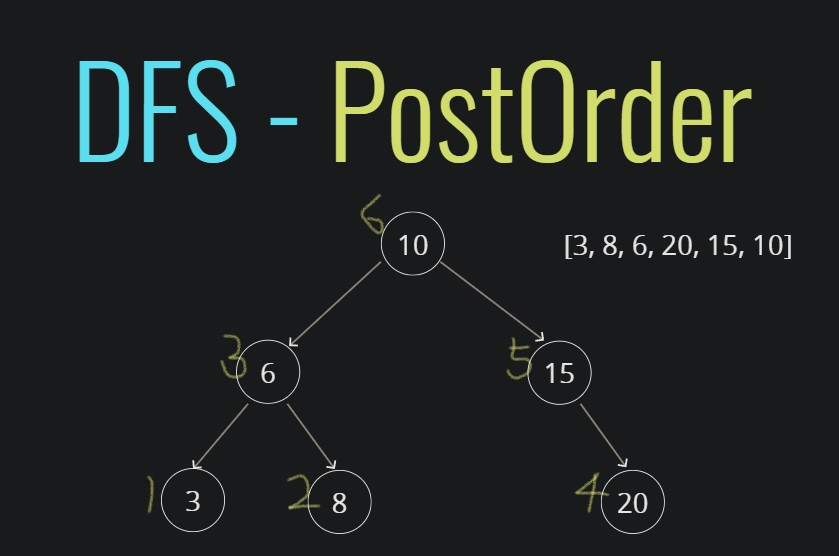
DFSPostOrder(){
        var data = [];
        function PostOrder(node){
            if(node.left) PostOrder(node.left);
            if(node.right) PostOrder(node.right);
            data.push(node.value);
        }
        PostOrder(this.root);
        return data;
    }

각각의 방법들을 언제 쓰면 좋을까?

• 언제 BFS를 쓰고 언제 DFS(전위,중위,후위)를 써야 하나?
  • BFS나 DFS는 모두 모든 노드들을 한번씩 방문하기 때문에 시간복잡도는 동일하다. 차이는 공간복잡도에 있다.

• 위와 같이 추적해야 할 노드가 넓게 퍼져서 많은 경우에 BFS(너비우선탐색)을 사용하면, 트리를 가로지르면서 Queue에 데이터를 다 저장해야 해서 결국 많은 데이터가 저장되어 공간복잡도가 높아진다.

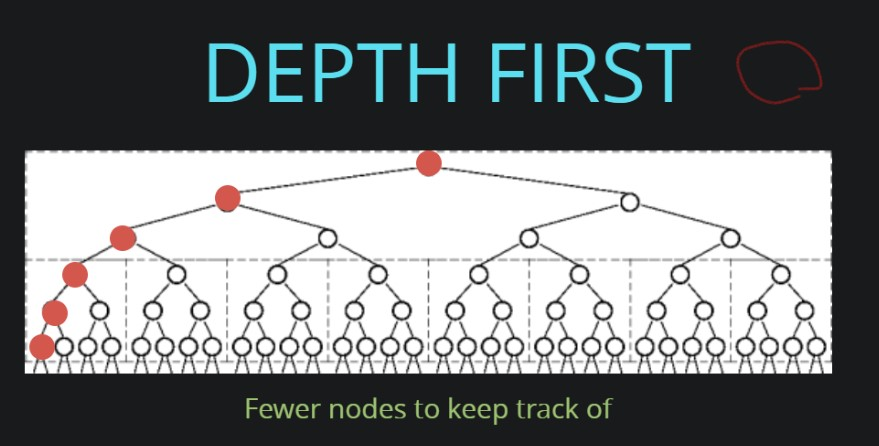
• 반면 위와 같이 동일한 데이터 형태에 DFS(깊이우선탐색)를 사용하면, 트리를 가로지르지 않고 수직으로 내려가며 재귀를 이용하므로 추적해야 하는 노드가 더 적다. 빨간색 점 각각에서 재귀가 발생하여 호출 스택의 한 칸이 된다.
• 즉, 이런 식으로 세로로 깊지 않고 가로로 넓은 트리의 경우에는 DFS(깊이우선탐색)가 BFS(너비우선탐색)보다 더 적은 공간을 점유하므로, DFS를 사용하는 것이 적절하다.
• 반대로 가로는 좁고 세로로만 아주 깊은 트리라면, BFS(너비우선탐색)가 DFS(깊이우선탐색)보다 더 적은 공간을 점유하므로, BFS를 사용하는 것이 적절하다.

DFS 전위,중위,후위 선택 방법은?

• 이진탐색트리에서 DFS-중위 탐색을 하면, 모든 노드가 오름차순 순서대로 나오게 된다. 예를 들어서, 리스트를 받아서 데이터베이스에 넣어야 한다던가 순서대로 무언가 작업을 해야 하는 경우 도움이 될 수 있다. 물론 이진탐색트리에서 가능한 방법이다.
• DFS-전위 탐색은 root부터 하위 child로 순차적으로 순회하므로, 트리를 외부에 저장했다가 나중에 다시 트리를 그대로 구성해야 하는 경우에 도움이 된다.