이상 탐지(Anomaly Detection)
정의
이상탐지(Anomaly Detection)이란?
- 정상(normal) 샘플과 비정상(abnormal, 이상치, 특이치) 샘플을 구별해내는 문제
분류
학습 시 비정상 샘플의 사용여부 및 라벨 유무에 따른 분류
1. 지도학습 기반 이상 탐지
- 주어진 학습 데이터 셋에 정상 샘플과 비정상 샘플의 데이터와 라벨이 모두 존재하는 경우
- 높은 정확도를 요구하는 경우 주로 사용됨
- 산업 현장에서는 비정상 샘플의 발생 빈도가 현저히 적기 때문에 클래스 불균형 문제가 심함
- 데이터 증강, 손실함수 재설계, 배치 샘플링 등의 기법 적용
2. 반지도학습(단일 클래스) 기반 이상 탐지
- 클래스 불균형이 심한 경우 정상 샘플만 이용해서 학습
- 정상 샘플들을 둘러싸는 discriminative boundary를 설정하고 boundary를 최대한 좁혀 밖에 있는 샘플들을 모두 비정상으로 간주
- One-Class SVM, Deep SVDD, Energy-based, Deep Autoencoding Gaussian Mixure Model, GAN, Self-Supervised Learning
3. 비지도학습 기반 이상 탐지
- 대부분의 데이터가 정상 샘플이라는 가정 하에 라벨 없이 학습시키는 방법론
- PCA, Autoencoder를 이용하여 차원을 축소하고 복원하는 과정을 통해 비정상 샘플을 검출
- 정확도가 다소 불안정
비정상 샘플의 정의에 따른 분류
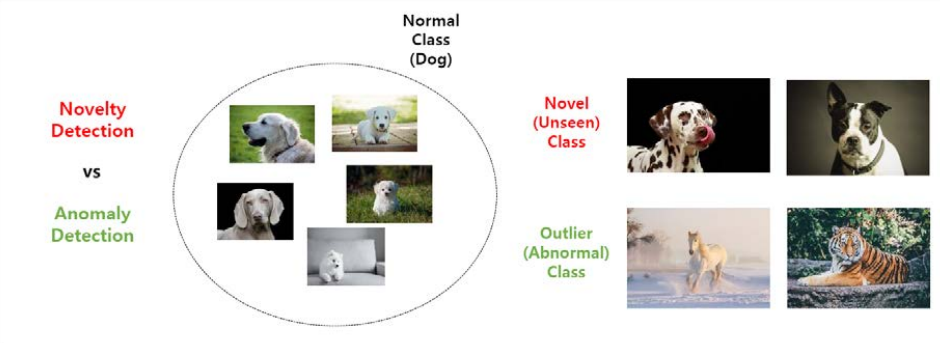
1. Novelty Detection
- 보유 중인 데이터 셋에 이전에 없던 형태의 새로운 개(Novel sample, Unseen sample)가 등장하는 경우 이러한 샘플을 찾아내는 방법론
2. Outlier Detection
- 새로운 샘플이 등장했을 때, 개가 아닌 호랑이, 말, 운동화, 비행기 등 개와 전혀 관련이 없는 샘플이 등장하는 경우
정상 샘플의 클래스 개수에 따른 분류(Ood Detection)
- 정상/비정상 대신 In-distribution/Out-of-distribution 샘플이라는 표현 사용
- In-distribution 데이터 셋으로 network를 학습시킨 뒤, test 단계에서 비정상 샘플을 찾는 문제
머신러닝 기반 이상 탐지
분류 기반 이상 탐지 기법
- 분류기를 Feature space에서 학습시킬 수 있다고 가정
- 라벨의 개수에 따라 One-class 혹은 Multi-class로 데이터를 학습
- Class에 해당하지 않는 개체를 이상치로 처리
- 오토인코더, 베이지안 네트워크, 서포트 벡터 머신, 결정 규칙 기반 등이 있음
1. 오토인코더
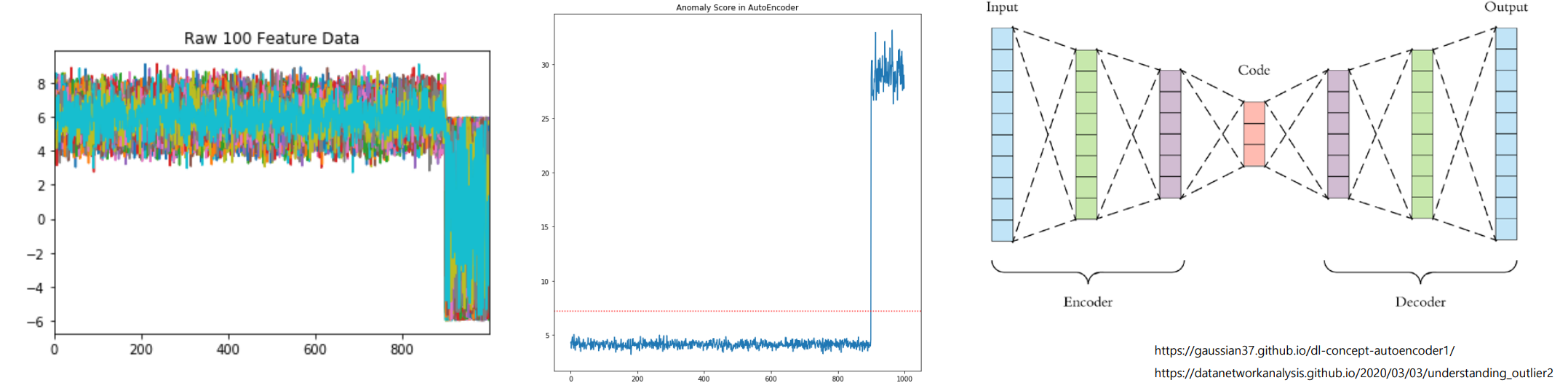
- 비지도학습 기반 모델
- 하나 이상의 은닉층으로 구성된 인코더를 통해 입력 데이터를 압축(차원 축소)
- 디코더를 사용해 개체를 복원(생성 모델)
- 복원했을 때 발생하는 복원 오차(reconstruction error)가 클수록 이상 개체라고 판단(이상 점수)
2. 베이지안 네트워크 기반

- Multi-class 문제에 사용
- 나이브 베이지안 네트워크로 테스트 데이터 내 관측값의 각 정상 클래스와 이상 클래스에 대한 사후 확률을 추정해 가장 높은 확률에 해당하는 클래스로 지정
- 각 클래스의 사전확률과 조건부확률은 훈련 데이터를 사용하여 추정해야 함
- 확률이 0으로 나오는 경우, Laplace Smoothing으로 0 대신 1 또는 적절한 양수값으로 부여
3. 서포트 벡터 머신 기반
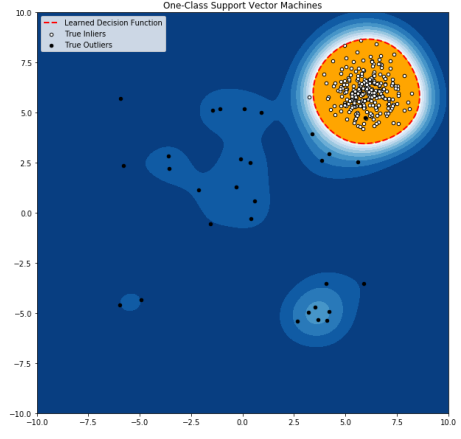
- One-class 문제에 사용
- 훈련 데이터를 포함하는 영역을 학습
- 결정 경계에만 초점을 맞추고 경계의 내외부에서의 분포에는 관심을 갖지 않음
- 영역의 구분이 복잡해지면 RBF(Radial Basis Function) 같은 커널 함수를 사용하기도 함
- 어떤 커널을 사용해야 할지 결정해야 함
4. 결정 규칙 기반
- 정상 자료를 판단하는 규칙들을 학습하고, 어떤 규칙에도 해당하지 않는 관측값을 이상으로 취급함
- Multi-class, One-class 모두 적용할 수 있음
- 훈련 데이터에 Decision Tree 등의 결정 규칙 학습 알고리즘을 이용해 규칙을 학습
5. NN 기반 이상 탐지 기법
- 정상치가 어떤 근방에 밀집되어 있고, 이상치가 각 근방에서 멀리 떨어져 있다는 가정
- 두 개체 사이의 거리 개념이 정의되어야 함
- 연속형 변수: 유클리드, 맨하튼, 민코프스키, 표준화, 마할라노비스 거리
- 범주형 변수: 단순 일치 계수(자카드 거리)
- 다변량 데이터: 각 변수에 대한 거리를 결합하여 사용
- 비지도학습 또는 준지도학습 기반
- 이상 점수를 구하는 방법
- k번째로 가까운 개체와의 거리를 이용(K-NN 기반)
- 상대밀도(Relative Density)를 이용(상대 밀도 기반)
1. K-NN 기반
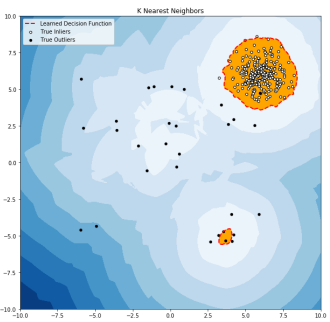
- 이상 점수를 k번째로 가까운 개체와의 거리로 정의하는 방법
- 이상 점수의 경계값(threshold)을 설정
- 이상 점수를 기준으로 정렬시킨 뒤 이상 점수가 가장 큰 m개를 이상값으로 보는 방법도 존재
- 연속형이 아닌 데이터 처리를 위해 다른 거리 척도를 도입: 가장 가까운 k개 개체와의 거리의 합, 한 개체에서 일정 거리 이내에 있는 개체의 수를 세는 방법, 데이터를 군집화한 뒤 군집 안에서 k번째로 가까운 이웃과의 거리를 구함, 거리의 최소/최대값을 이용하여 가장 이상한 k개의 개체를 포함하지 않을 만한 군집은 제거하고 나머지에서만 이상값을 찾아냄
2.상대 밀도 기반
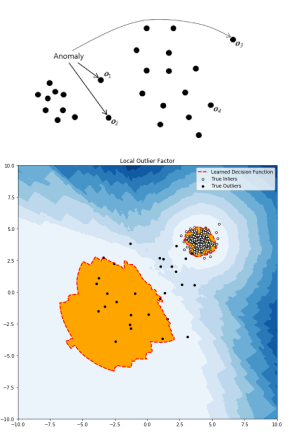
- 각 관측값 근방의 밀도를 추정하여 근방의 밀도가 낮은 관측값은 이상값이라 판단함
- 영역에 따라 밀도가 다를 때 취약함 -> 해결하기 위해 Local의 상대적인 밀도를 비교하여 이상값을 정하는 LOF(Local Outlier Factor) 기법이 등장함
- 가장 가까운 k개 점들의 local density의 평균이 자기 자신의 local density의 비율로 정의됨
- 밀집된 클러스터에서 조금만 떨어져 있어도 이상치로 탐지함
- 판단하는 기준은 도메인 지식을 이용해 경계값을 결정해야 함
군집화 기반 이상 탐지 기법
- 비지도학습 방법
- 3가지 가정
- 정상값들은 하나 또는 몇 개의 군집에 모여 있고, 이상값은 군집에 속하지 않음
- 군집의 중심 중 가장 가까운 것과 거리가 짧으면 정상값, 멀면 이상값임
- 정상값은 크거나 조밀한 군집에, 이상값은 작거나 희소한 군집에 속함
- 이상값이 군집을 이루는 경우 취약해짐
- 다수의 군집화 알고리즘이 모든 관측값의 군집을 지정하기 때문에 이상값이 큰 군집에 들어가 정상값으로 판단될 수 있음
- 거리 계산이 필요한 점은 NN기반 이상 탐지 기법과 유사함
- 군집화 기반 이상 탐지 기법은 자신이 속한 군집과 관련하여 각 관측치를 평가한다면, NN기반 이상 탐지 기법은 가까이 존재하는 로컬 이웃에 대해 각 관측치를 분석함
가정 1
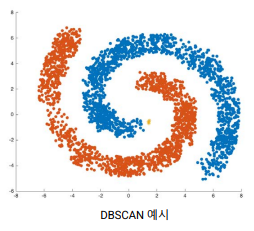
정상값들은 하나 또는 몇 개의 군집에 모여 있고, 이상값은 군집에 속하지 않음
- 모든 관측값을 군집에 넣지 않아도 되는 DBSCAN, ROCK, SNN 군집화 알고리즘을 사용
- 데이터에서 군집을 찾아낸 뒤 제거하고 나머지를 이상값으로 처리함
- 군집을 찾아내는 것이 주된 목적이기 때문에 이상탐지에 최적화되어 있지 않음
가정 2
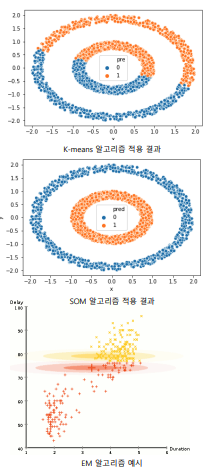
군집의 중심 중 가장 가까운 것과 거리가 짧으면 정상값, 멀면 이상값임
- 군집화를 수행하고 관측값이 포함된 군집의 중심과 관측값 사이의 거리를 이상 점수로 정의
- SOM, k-Means Clustering, EM algorithm
- 훈련데이터를 군집화하고 테스트데이터를 군집과 비교해 이상점수를 얻는 방식으로 준지도학습 방법이 될 수 있음
- 이상값들이 군집을 이룰 때 성능이 떨어짐
가정3
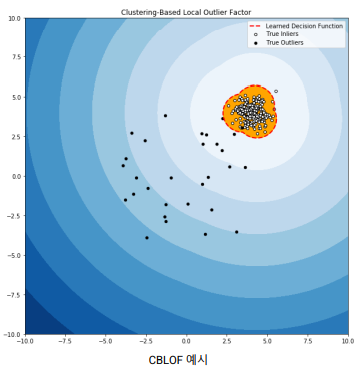
정상값은 크거나 조밀한 군집에, 이상값은 작거나 희소한 군집에 속함
- 관측값이 속한 군집의 크기나 밀도가 이상 여부를 판단하는 기준임
- FindCBLOF: 관측값이 속한 군집의 크기 및 관측값과 그 군집의 중심 사이의 거리를 반영하는 방법
통계적 기법
- 근본원칙: 이상값은 가정된 확률분포에서 생성되지 않아 부분적으로, 또는 완전히 동떨어졌다고 여겨지는 관측값
- 이상값은 확률분포에서 낮은 영역에서 나타난다고 가정함
- 검정통계량을 바탕으로 학습된 모형으로부터 생성되었을 확률이 낮은 관측값을 이상값으로 봄
- 모수, 비모수적 기법 모두 적용할 수 있음
1. 모수적 기법
- 정규분포 기반
- 최대가능도추정법으로 모수 추정
- 각 관측값과 추정된 평균 사이의 거리가 이상점수
- Grubb's Test
- 회귀모형 기반
- 회귀모형 적합 후 테스트 관측값의 잔차로 이상점수 산출
- 훈련 데이터에 이상값이 존재하면 영향을 받음
- Robust 회귀를 통해 이상값을 가려냄과 동시에 발견 가능
- 혼합모수적 모형 기반
- 데이터에 모수적 분포들을 혼합한 모형을 이용
- 정상값과 이상값에서 서로 다른 분포를 부여하거나 정상값에만 혼합분포를 주는 방법이 있음
2. 비모수적 기법
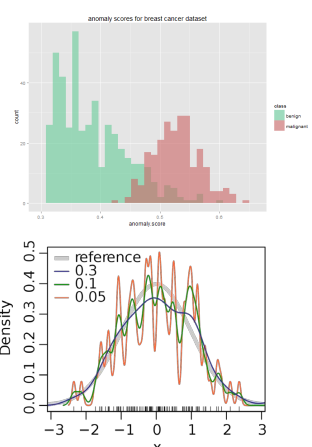
- 히스토그램 기반
- 훈련데이터로 히스토그램을 생성한 뒤 테스트 관측값이 유의미한 구간에 포함되면 정상, 그렇지 않으면 이상으로 판단
- 관측값이 포함되는 구간의 빈도를 바탕으로 이상점수를 구하기도 함
- 데이터가 다변량이면 각 변수에 대한 히스토그램으로 이상점수를 구한 뒤 합산하여 총 이상점수를 구함
- 커널함수 기반: 비모수적 밀도함수 추정기법, Parzen Window
스펙트럴 기법
- 변수들의 조합으로 자료의 변동을 대부분 설명하도록 근사
- 데이터를 더 낮은 차원의 부분공간으로 보내면 그 공간에서는 정상과 이상이 확연히 구분된다는 가정을 전제로 함
- 주성분 분석
- 데이터를 저차원 공간으로 사영시켰을 때, 데이터의 상관구조를 만족하는 정상개체는 사영값이 낮고, 상관구조를 벗어난 이상개체는 높은 값을 보이게 되는 방식
- 고차원 데이터 처리에 적합함
시계열 데이터의 이상 탐지
-
시계열 데이터에서 이상의 유형은 contextual anomalies가 자주 발견됨
-
context는 보통 시간적 특성을 의미함
-
이상의 유형
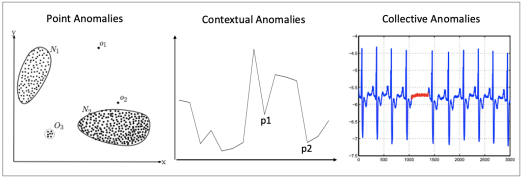
- Point anomalies: 개별적인 데이터 instance가 다른 데이터의 범주와 많이 벗어나는 것
- Contextual anomalies: instance 그 자체로는 다른 데이터의 값의 범주에서 벗어나지 않지만 특정한 context에서 변칙적인 것으로 여겨질 때
- Collective anomalies: 데이터 집합이 전체 데이터 집합과 비교하여 다른 유형인 경우
-
시계열 데이터의 이상 탐지에서는 전후 instance, context를 같이 고려해야 함
- Additive outliers: 짧은 기간에 급등하면 생기는 뾰족한 부분(e.g website에서 사용자의 수가 짧은 기간에 갑자기 증가한 경우)
- Temporal changes: website가 다운되어서 사용자의 수가 0에 가까워진 것과 같은 종류의 이상치
- Level shifts 또는 seasonal level shifts: 몇몇 conversion funnel을 다루다 보면 변화가 생겨 구매 전환율이 떨어지는 경우와 같은 이상치
-
Autoencoder 등의 이상 탐지 알고리즘과 RNN, LSTM 등 시퀀스 데이터 처리가 가능한 알고리즘을 결합하여 사용
-
RNN 등의 네트워크는 입력값으로 개별적인 instance 대신 sequence를 사용할 수 있어 시간적인 특성을 고려하여 이상치를 탐지해낼 수 있음
STL Decomposition
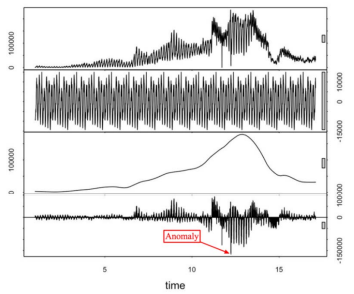
- STL: Loess에 기반한 Seasonal-trend decomposition
- Loess
* 국소회귀- 대표하는 포인트별로 회귀를 적합시킨 후 모델을 생성하는 비선형 회귀 알고리즘
- 시계열 데이터를 seasonal, trend, residue의 3개의 part로 분해할 수 있음
- 간단하고 robust함
- 많은 다른 상황에 적용 가능하고 모든 이상치들을 직관적으로 해석 가능함
- Additive outliers를 탐지하는 데 특히 좋음
- 데이터의 특성이 급격히 변할 때 잘 작동하지 않음
SH-ESD
- Seasonal Hybrid ESD(Extreme Studentized Deviate)
- STL을 사용해 seasonality와 trend의 영향을 제거함
- MAD, Grubb's test 등 robust한 metric을 사용함
- MAD(Median Absoulte Deviation)
* 관측값에서 중앙값을 뺀 값들의 중앙값- 표본분산보다 이상치에 덜 영향을 받는 분산 측정 방법
- Grubb's test(=ESD test): 정규분포 가정 하에 단일 이상치를 탐지하는 방법
- Generalized ESD
* 여러 개의 이상치를 가정한 검정방법- 정규성을 가정하고 있기 때문에 정규성 테스트를 먼저 해야 함
- 계절성을 고려하지 않음 -> STL 먼저 수행
ARIMA(Auto-regressive Integrated Moving Average)
-
AR(Autoregression) 모형 + MA(Moving Average) 모형
-
시계열 데이터의 정상성(Stationary)를 가정함
-
정상성: 평균, 분산이 시간에 따라 일정한 성질, 시계열 데이터의 특성이 시간의 흐름에 따라 변화히지 않음을 의미함
-
정상 시계열 변환
- 변동폭이 일정하지 않은 경우: 로그 변환
- 추세, 계절성이 존재하는 경우: 차분(differencing), 1차 차분으로 정상성을 띄지 않으면, 차분을 반복함
-
AR 모형: 이전 자신의 관측값이 이후 자신의 관측값에 영향을 준다는 아이디어에서 기반함
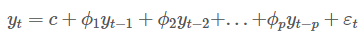
-
MA 모형: 예측 오차를 이용하여 미래를 예측하는 모형
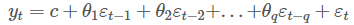
-
ARIMA 모형: d차 차분한 데이터에 위 AR(p) 모형과 MA(q) 모형을 합친 모형
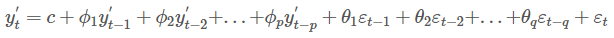
-
과거의 point들을 통해, 다음 point의 예측에 white noise라고 불리는 확률변수를 더해서 예측을 생성하는 방식
-
이렇게 예측된 point들은 다시 다음 point의 예측에 auto-regressive하게 이용됨
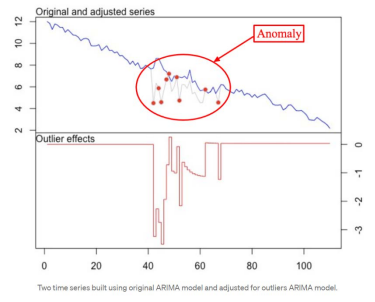
-
Signal의 adjusted series를 만들어 original series와의 비교를 통해 이상치를 탐지함
-
Autoregression의 차수(p), 차분의 수(d), forecast error coefficient(q)를 선택해야 함
-
Signal이 차분 후에도 정상성을 유지해야 함
Exponential Smoothing
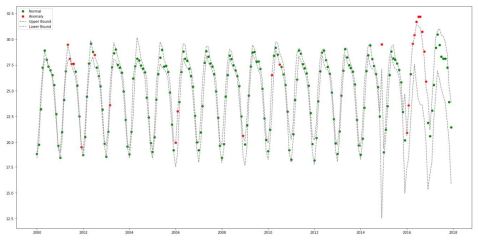
- ARIMA와 유사하게 Trend, Level, Seasonality를 활용하지만, 최근의 결과값에 더 가중치를 준다거나 줄일 수 있음
- SES(Single Exponential Smoothing): 단순히 Trend와 Level만 참조
- Holt-Winters 모델: Trend, Level, Seasonality 같이 고려
- Brutlag 알고리즘으로 신뢰구간을 계산하여 정상치과 이상치를 구별할 수 있음
Classification and Regression Trees(CART)
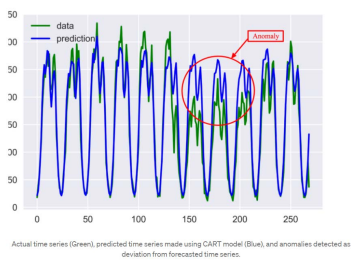
- 가장 널리 사용되는 의사결정나무 알고리즘
- 머신러닝 기법 중 가장 robust하고 효과적인 기법 중 하나
- 실제 데이터 그래프와 예측 그래프의 편차가 큰 부분을 이상치로 판단
- Signal의 어떠한 구조에도 묶여있지 않음
- 많은 feature parameter들을 학습에 이용해서 더욱 정교한 모델을 얻을 수 있음
LSTM 기반 이상탐지
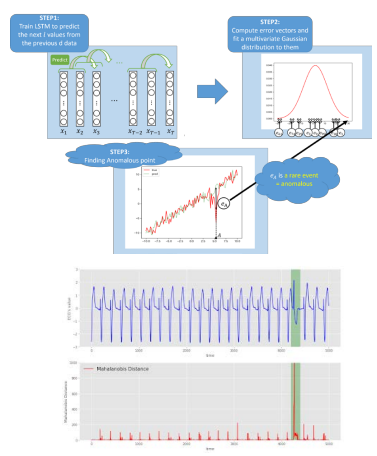
- 시계열 데이터의 과거값들을 이용해, 한 단계 바로 뒤의 값들을 예측하도록 모델 학습
- 오차벡터를 계산하고 다변량 가우스 분포를 오차벡터에 적합시킴
- 예측값과 실제값의 오차가 가우스 분포의 끝 부분에 위치해 있다면 이상치로 판단함
- 분포 내 예측과 오차에 대한 희소한 양을 표시하기 위해 마할라노비스 거리를 사용함
LSTM-Autoencoder
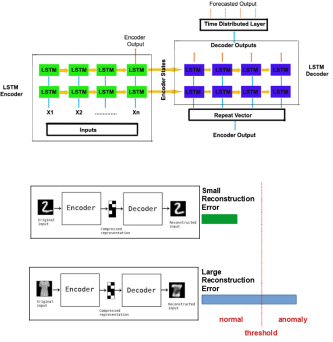
- RNN 장점 중 하나는 이전의 정보를 현재의 문제해결에 활용할 수 있음
- Vanishing gradient 문제를 해결하기 위해 LSTM이 주로 사용됨
- Autoencoder: 비정상 데이터가 거의 없거나, 존재하지 않는 상황에서도 적용시킬 수 있음
- 기존의 오토인코더는 시간적 특성을 담을 수 없으므로, LSTM층을 이용해 오토인코더를 구성함
- 이상치 데이터가 모델에 입력되면 복원 에러가 굉장히 높게 나옴
- 산출한 에러를 그래도 사용하면 정상적인 경우에서 에러값이 급격하게 증가하는 경우가 있기 때문에 EWMA를 사용해 smoothing 후 사용함
- Dynamic Error Thresholds
- 에러 셋을 통해 threshold를 산출하고 적용시킴
- 각 에러 셋에 따라 threshold가 달라질 수 있음
- 에러 셋을 기반으로 threshold를 산출하기 때문에 편리하고 정확함

잘 정리되어 있는 글 잘 읽었습니다~