Matrix

1학년 공수, 선대 이후로 수학 지식들이 삭제됐다.. 되새기는 겸으로 numpy 기호들과 기록.

Annotation

scalar calculation

numpy에서 +, - 가능.

scalar product

Hadmard Product : 은 모양의 vector끼리 성분곱하는 것
X · Y

X * Y

Norm

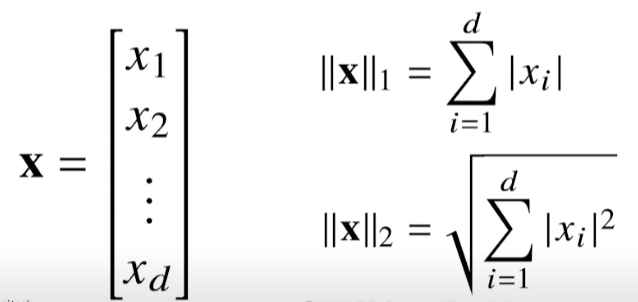
원점에서부터 벡터까지의 거리.
L1 norm = 변화량의 절대값의 합
L2 norm = 유클리드 거리

Vector 사이의 각도

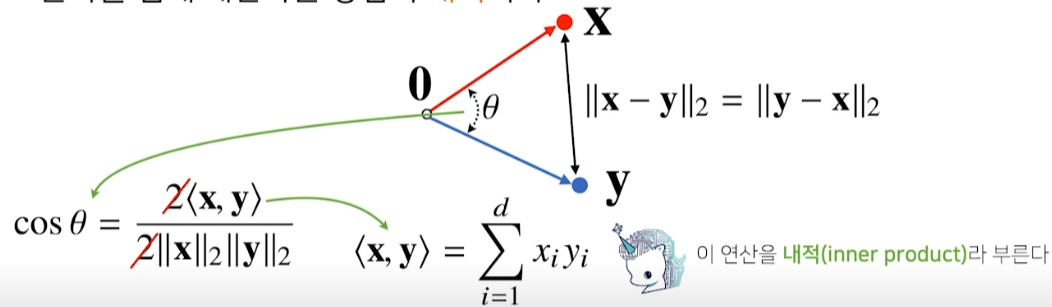
제2 코사인 법칙을 사용해, 두 벡터 사이의 각도 계산 가능.

def angle(x, y):
    v = np.inner(x, y) / (l2_norm(x) * l2_norm(y))
    theta = np.arccos(v)
    return theta

multiplication

XY

X @ Y

행렬곱을 통해 Matrix를 벡터 공간에서의 operator로 이해할 수도 있다. 행렬곱으로 벡터를 다른 차원의 벡터로 보낼 수 있기 때문.
즉, 패턴 추출, 데이터 압축에 사용 가능.

inner product

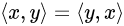
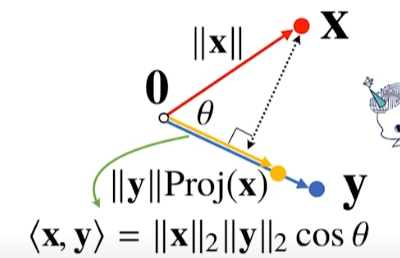
inner in numpy

np.inner는 벡터간의 내적이다. 벡터간의 내적을 행렬에서 표현하고자 하면 보통 Transpose를 활용해서 수식으로 표현한다.

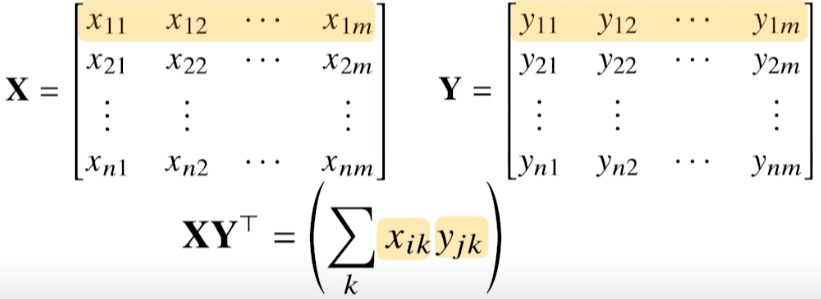
np.inner(X, Y)

Inverse matrix

np.linalg.inv(X)

Pseudo-inverse(유사역행렬), Moore-Penrose 행렬

• 역행렬과 다르게 행과 열의 수가 반드시 고정되지 않는다.
• 그럼에도 역행렬과 유사한 역할을 한다.
  
  n = 행, m = 열

np.linalg.pinv(X)

연릭방정식 풀이

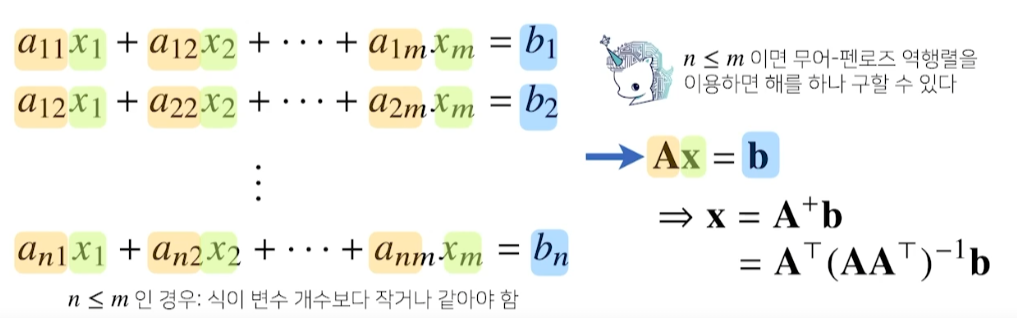
선형회귀분석

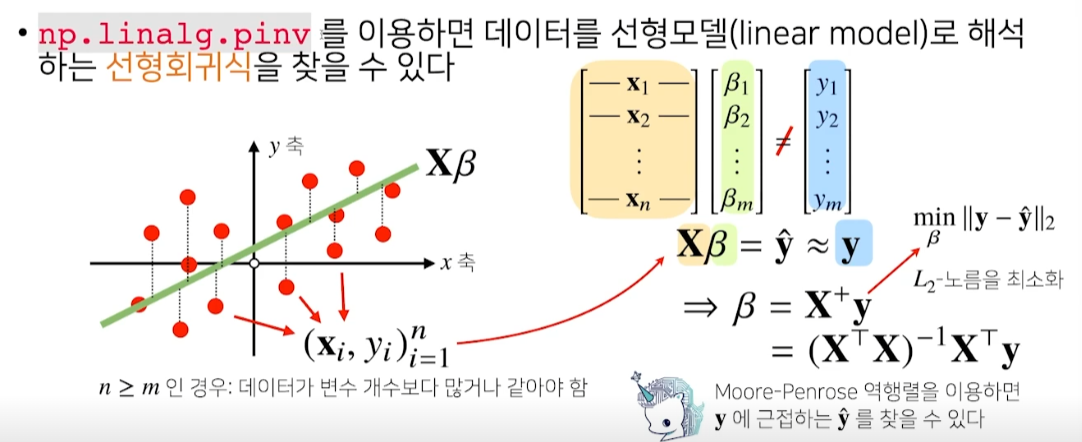
데이터의 분포를 고려하면 연립방정식처럼 선형회귀분석을 하는 것은 불가능하다.
따라서, y의 L2 norm을 최소화하는 방향으로 해를 찾는 것이 일반적이다.

# using sklearn for linear regression
from sklearn.linear_model import LinearRegression
model = LinearRegression()
model.fit(X, y)
y_test = model.predict(x_test)

# Moore-Penrose inverse matrix
X_ = np.array([np.append(x, [1]) for x in X]) # y절편(intercept) 추가
beta = np.linalg.pinv(X_) @ y
y_test = np.append(x_test) @ beta

sklearn에서 linear regression시에 y 절편을 자동으로 추정해서 계산한다.
Moore-Penrose 역행렬을 통해서 선형회귀를 할 때, 직접 y 절편을 추가해서 X를 구성해야 한다.