[Lv.2] 리코쳇 로봇

https://school.programmers.co.kr/learn/courses/30/lessons/169199

문제 설명

리코쳇 로봇이라는 보드게임이 있습니다.

이 보드게임은 격자모양 게임판 위에서 말을 움직이는 게임으로, 시작 위치에서 목표 위치까지 최소 몇 번만에 도달할 수 있는지 말하는 게임입니다.

이 게임에서 말의 움직임은 상, 하, 좌, 우 4방향 중 하나를 선택해서 게임판 위의 장애물이나 맨 끝에 부딪힐 때까지 미끄러져 이동하는 것을 한 번의 이동으로 칩니다.

다음은 보드게임판을 나타낸 예시입니다.

. . . D . . R
. D . G . . .
. . . . D . D
D . . . . D .
. . D . . . .

여기서 "."은 빈 공간을, "R"은 로봇의 처음 위치를, "D"는 장애물의 위치를, "G"는 목표지점을 나타냅니다.
위 예시에서는 "R" 위치에서 아래, 왼쪽, 위, 왼쪽, 아래, 오른쪽, 위 순서로 움직이면 7번 만에 "G" 위치에 멈춰 설 수 있으며, 이것이 최소 움직임 중 하나입니다.

게임판의 상태를 나타내는 문자열 배열 board가 주어졌을 때, 말이 목표위치에 도달하는데 최소 몇 번 이동해야 하는지 return 하는 solution함수를 완성하세요. 만약 목표위치에 도달할 수 없다면 -1을 return 해주세요.

제한사항

• 3 ≤ board의 길이 ≤ 100
  • 3 ≤ board의 원소의 길이 ≤ 100
  • board의 원소의 길이는 모두 동일합니다.
  • 문자열은 ".", "D", "R", "G"로만 구성되어 있으며 각각 빈 공간, 장애물, 로봇의 처음 위치, 목표 지점을 나타냅니다.
  • "R"과 "G"는 한 번씩 등장합니다.

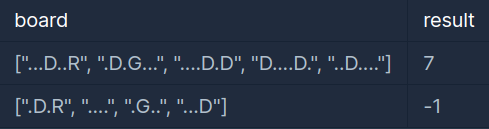
입출력 예

문제 풀이

해당 문제는 기존 BFS와 방식이 거의 같아서 크게 특별할 것이 없는 문제이다.
시작 위치에서 목표 위치까지 가는 방식에서 미끄러지는 로직을 추가만 하면 된다.
유의할 점은 가장 처음 시작 위치 또는 벽에 막혀 더이상 미끄러지지 않을 때만 Queue 에서 노드를 꺼내야 한다는 점이다.

풀이 코드

class Node {
    int x;
    int y;
    int[] currentDirection;
    int count;

    public Node(int x, int y, int[] currentDirection, int count) {
        this.x = x;
        this.y = y;
        this.currentDirection = currentDirection;
        this.count = count;
    }
}

class Solution {
    public int solution(String[] board) {
        int answer = -1;
        Queue<Node> bfsQueue = new LinkedList<>();
        boolean[][] visited = new boolean[board.length][board[0].length()];
        int[] startPosition = new int[2];
        int[] xDirection = {0, 0, 1, -1};
        int[] yDirection = {1, -1, 0, 0};

        // find start position
        for (int i = 0; i < board.length; i++) {
            for (int j = 0; j < board[i].length(); j++) {
                if (board[i].charAt(j) == 'R') {
                    startPosition[0] = i;
                    startPosition[1] = j;
                }
            }
        }

        // BFS
        bfsQueue.add(new Node(startPosition[0], startPosition[1], new int[]{0, 0}, 0));

        while (!bfsQueue.isEmpty()) {
            // 미끄러져 이동
            Node peekNode = bfsQueue.peek();
            if (peekNode.currentDirection[0] != peekNode.currentDirection[1]
                    && isSafePath(peekNode.x + peekNode.currentDirection[0], peekNode.y + peekNode.currentDirection[1], board)) {
                peekNode.x += peekNode.currentDirection[0];
                peekNode.y += peekNode.currentDirection[1];
                continue;
            }

            Node node = bfsQueue.poll();

            // 목표 도달 체크
            if (board[node.x].charAt(node.y) == 'G') {
                answer = node.count;
                break;
            }

            if (visited[node.x][node.y]) continue;
            visited[node.x][node.y] = true;

            // 방향 전환
            for (int i = 0; i < 4; i++) {
                int x = node.x + xDirection[i];
                int y = node.y + yDirection[i];

                if (!isSafePath(x, y, board)) {
                    continue;
                }

                bfsQueue.add(new Node(x, y, new int[]{xDirection[i], yDirection[i]}, node.count + 1));
            }
        }

        return answer;
    }

    private boolean isSafePath(int x, int y, String[] board) {
        return x >= 0 && x < board.length && y >= 0 && y < board[x].length() && board[x].charAt(y) != 'D';
    }
}