Image Classification

Image Classification이란 이미지를 넣으면 시스템은 미리 정해진 레이블들 중에서 하나를 선택해서 출력하는 것이다. 사람의 입장에서는 이 과정이 매우 쉬운 작업으로 보이지만, 컴퓨터에게 이미지는 거대한 숫자 격자일 뿐이며 수천 또는 그 이상의 배열이지 고양이 이미지에서 고양이를 추출하는 것은 매우 어렵다.

Semantic Gap

컴퓨터가 표현하는 방식이 우리에게 목적(여기에서는 image classification)을 완수할 수 있도록 하는 영감을 주지 못한다는 것을 말한다.
왜 영감을 주지 못하는 걸까? 그건 우리가 보기에는 작은 변화임에도 불구하고, 실제로 컴퓨터의 표현 방식으로 보면 완전히 다른 것으로 보이기 때문이다.
이 떄 완전히 다르게 보이게 하는 것은 무엇일까?
촬영 각도, 조명(Illumination), 객체의 변형(Deformation), 폐색(Occlusion), 배경 교란(background Clutter), 클래스 내부 변화(Intraclass Variation)가 있다.
따라서 알고리즘은 이 다양한 변형에 대응 가능해야 한다는 것이다.

Data-Driven Approach

edge를 감지하는 알고리즘을 사용하여 edge를 추출한 다음 코너나 다른 유형의 해석 가능한 패턴을 찾으려고 할 것이다. 인간이 아는 모든 것을 하드코딩하려고 하지만, 그것은 좋은 방법이 아니다.

그렇다면 좋은 방법은 무엇일까?
물체에 관해서 일일이 다 코딩할 수 없기에 데이터 기반 접근 방식을 사용하고 데이터에서 학습하는 알고리즘을 사용하는 것이다.

1. collect a dataset of images and lavels
2. Use Machine Learning to train a classifier
3. Evaluate the classifier on new images

따라서 훈련 함수와 예상 함수가 필요해졌다. 많은 데이터를 통해 훈련시킨 모델로 예상하는 구조가 Data-Driven Approach라 할 수 있겠다.

def train(images, labels):
	# Machine Learning!
    return model

def predict(model, test_images):
	# Use model to predict labes
    return test_labels

KNN(K-Nearest Neighbor)

KNN은 가까이에 있는 훈련이미지 예시들에 근거해서 라벨을 예측한다.

Hyperparameter

해당 사이트에서 K값과 Distance metric의 값에 따라 어떤 영향을 미치는지 테스트해볼 수 있다.

k

몇번째로 가까운 데이터까지 살펴볼 것인가

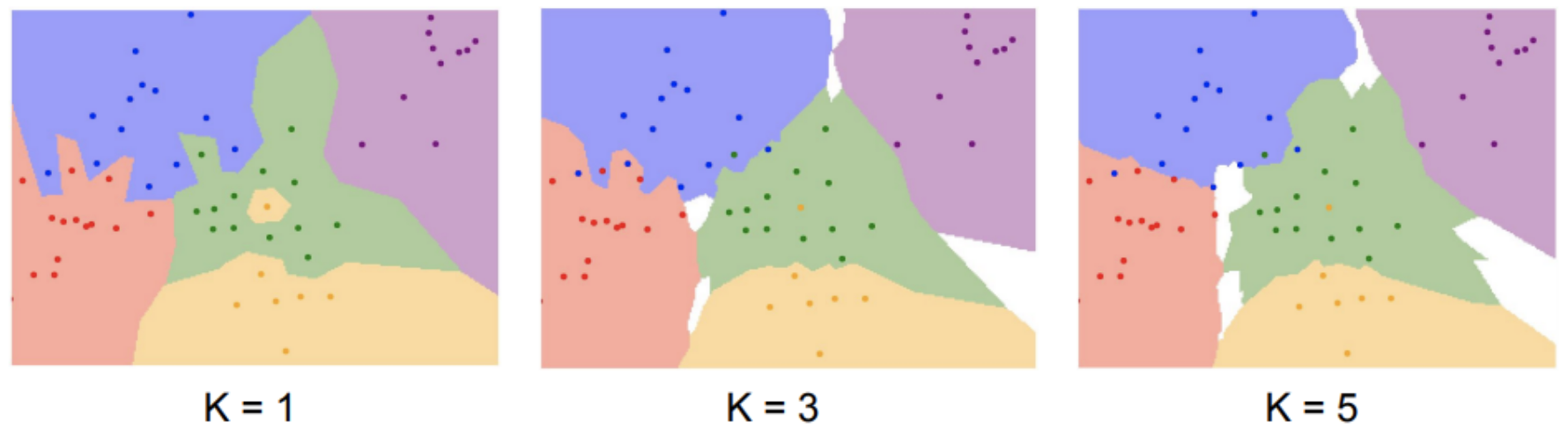
k=1이란, 각 좌표가 근처 이웃 1개랑 비교하여 카테고리를 나눈 것이다. 하지만 이미지에서도 보이는 것처럼 경계선들이 삐죽하거나 한 레이블 안에 다른 레이블이 들어가있는(초록 레이블 안 노란 레이블) 등 단점이 있다. 따라서 개선한 것이 k개 만큼의 가까운 이웃과 비교하여 가장 많은 레이블에 속한 레이블로 투표하여 정하는 방법이다.

Distance metric

각 좌표가 주변 좌표와 비교하는 과정에서 어떤 방식으로 할 것인가

• L1(Manhattan) distance
  
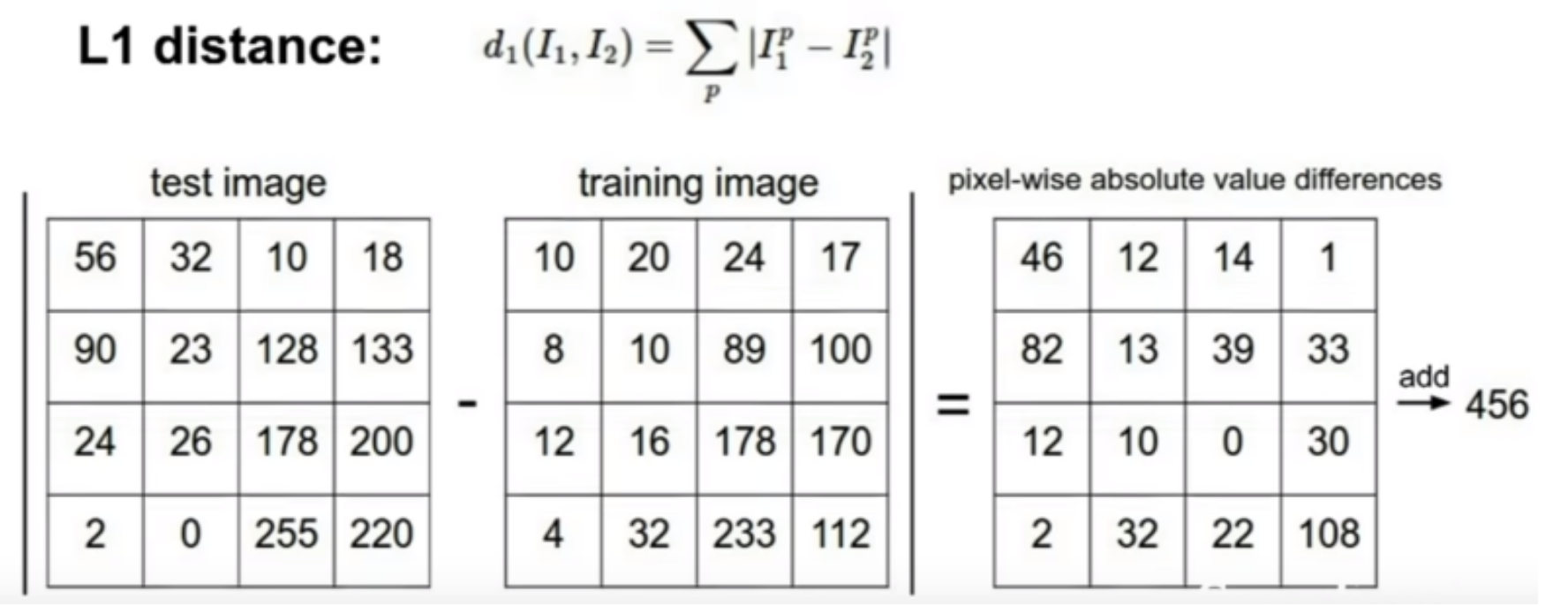
  테스트 이미지와 트레이닝 이미지의 각각 대응되는 픽셀들끼리 비교하여 각각의 distance(절대값)를 구하고, 이를 모두 더하여 최종 결과값을 출력한다.

• L2(Euclidean) distance
  테스트군 - 훈련군을 제곱한 것의 합에 대한 제곱근을 구하는 방식
  L1은 좌표계를 회전했을 때 실제 거리도 달라지는 반면, L2는 좌표계의 회전과 무관하게 거리가 일정하다. 많은 경우에 L2가 유용하다고 한다.

두 점 사이의 거리 공식(Distance Formula) 쉽게 이해하기

Hyperparameter 고려사항

• What is the best value of K to use?
• What is the best distance metric to use?

이러한 값들은 해결해야할 문제에 따라서, 문제에 정의된 데이터 타입에 따라서 모두 다르다. 이러한 사항들은 데이터로부터 추출할 수 있는 것이 아니라 설계자가 결정해주어야하는 문제이다. 하이퍼파라미터는 여러번 실험을 통해 그 중에서 가장 좋은 것으로 설정하는 것이 일반적이다.

1. 훈련셋에서 가장 좋은 결과를 내는 하이퍼파라미터를 설정하기 ❌

K=1, training data(훈련 셋)는 항상 완벽하게 분류하겠지만 test data(테스트 셋)는 잘못 분류하는 경우가 있을 수 있다. 궁극적으로 훈련셋보다 아직 label을 예측하지 못한 테스트셋에 대한 성능이 중요하다.

2. 훈련셋과 테스트셋 사전에 분리하기 ❌

훈련셋으로 다양한 하이퍼파라미터 값들을 학습을 시키고 테스트셋에 적용시켜본 다음, 하이퍼파라미터를 선택하는 경우이다. 아예 한번도 보지 못한 데이터에서 알고리즘의 성능을 측정해야하기 때문에 이 방법도 좋은 방법이 아니다. 이와 같이 한다면 그저 테스트셋에서만 잘 동작하는 하이퍼파라미터를 고른 것일 수 있다.

3. 데이터를 3등분으로 나누기

훈련셋(Train), 검증셋(Validation), 테스트셋(Test)으로 나누어, 훈련셋에서 다양한 하이퍼 파라미터로 알고리즘을 훈련시키고, 검증셋에서 평가하고, 검증셋에서 가장 잘 동작하는 하이퍼파라미터를 선택하는 것이다. 그리고 검증셋과 테스트셋을 엄격하게 분리 유지하는 것이 중요하다.

4. 교차검증

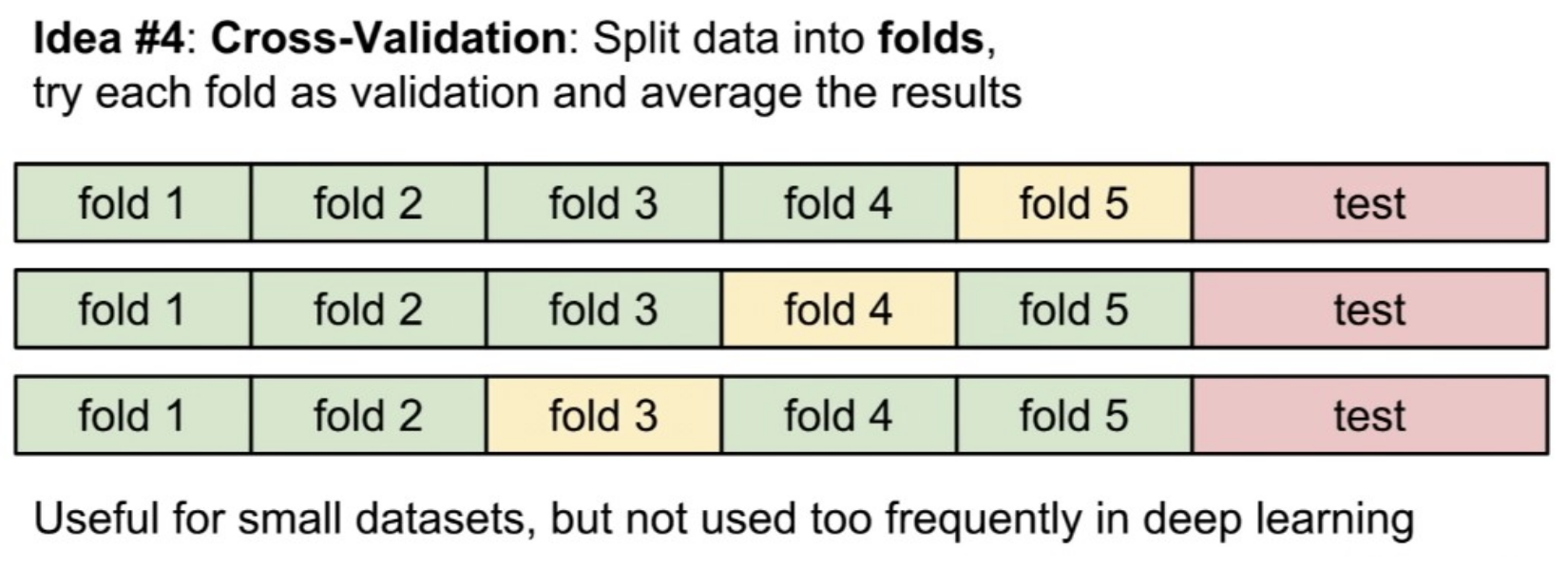
훈련셋을 여러개로 나누고 번갈아가면서 검증셋을 지정해준다.
데이터셋에서 먼저 테스트셋을 분리한 뒤, 나머지 데이터셋을 fold라는 단위로 나눈다. 그 후 fold들 중에 검증셋을 선택하는 과정을 반복한다.
위의 예제는 5개의 폴드 교차 검증이다. 먼저 fold 1-4에서 학습시키고 fold5에서 검증한다. 그 후 fold1-3,5에서 학습시키고 fold4에서 검증한다. 이처럼 반복하는 것을 볼 수 있다.
이를 통해 최적의 하이퍼파라미터를 얻을 수 있지만, 계산량이 많기 때문에 보통 작은 데이터셋일 경우 주로 사용하고, 딥러닝에서는 잘 사용하지는 않는다.

KNN의 단점

1. Curse of Dimensionality 차원의 저주 - 많은 훈련셋이 필요하다.
   
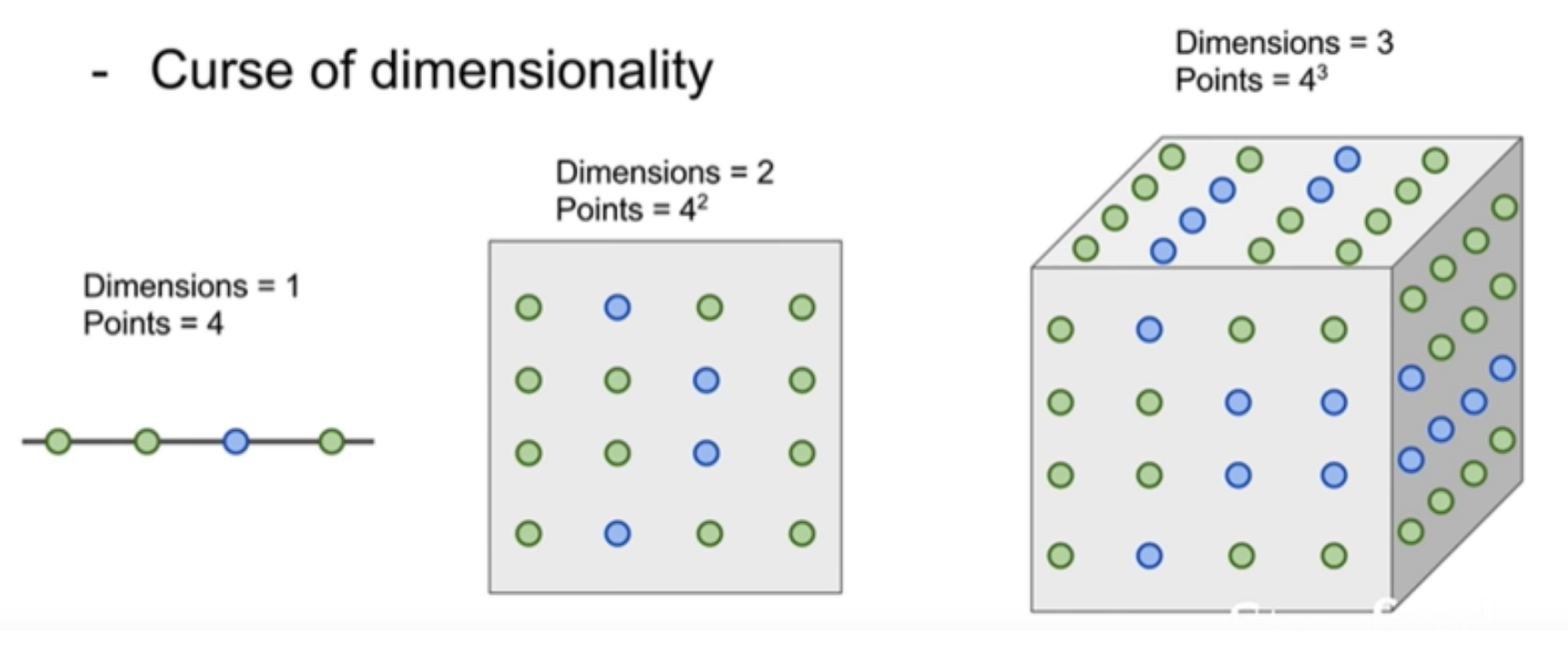
   만약 훈련셋이 적다면 새로 들어온 데이터와 제일 근접한 이웃 포인트가 실제로는 꽤 멀리 떨어져 있을 수 있기 때문이다. 즉 공간 안에 data point가 빽빽하게 들어가 있어야한다. 공간이 클수록 훈련셋은 많이 필요할테고 그 수가 기하급수적으로 늘어날 수 있다.

2. 테스트 시간이 너무 오래 걸린다.

3. L1이나 L2 기반의 유사도 측정 방식은 이미지 유사도 측정에 좋지 않은 방식이다.
   
   위의 이미지를 보면 원본이미지(가장 왼쪽)에서 조금씩 변형한 이미지들을 볼 수 있다. 이것을 L2로 유사도를 측정했을 때 원본이미지와의 거리가 모두 같다고 나온다. 즉 pixel단위의 유사도를 측정하는 것이 좋은 지표가 될 수 없다는 것으로 해석할 수 있다.

Question

Nearest Neighbor Classifier, With N examples, how fast is training?
Nearest Neighbor Classifier, With N examples, how fast is testing?
단순히 데이터를 기억하기만 하면 되기 때문에 훈련 복잡도는 O(1)이다.
훈련셋과 일일이 비교하는 과정이 들어가기 때문에 테스트 복잡도는 O(N)이다. (N=훈련셋)
사실 실제로 이렇게 서비스가 나온다면 그닥 좋은 서비스가 아닐 것이다. 학습은 느려도 괜찮지만 테스트 시점에는 빠르기를 원할테니까.

What is the best value of K to use?
알고리즘을 수행하기 전에 바로 알 수 있는 경우는 거의 없다. 때문에 여러가지 값들을 시도해보고 가장 좋은 값들을 찾아낸다.

What is the best distance metric to use?
L1 방식은 좌표계가 돌아가면 모양도 달라진다(좌표의존성). L2 방식은 돌아가도 모양에 아무 변화가 없다. 따라서 L1방식은 특징 벡터의 요소가 실질적인 의미를 가질 경우, L2 방식은 특징 벡터의 요소가 일반적이고 실질적인 의미를 모를 때 사용한다.
그럼 예를 들면?

참고 사이트
강의동영상