Parameter 기반의 접근 방식
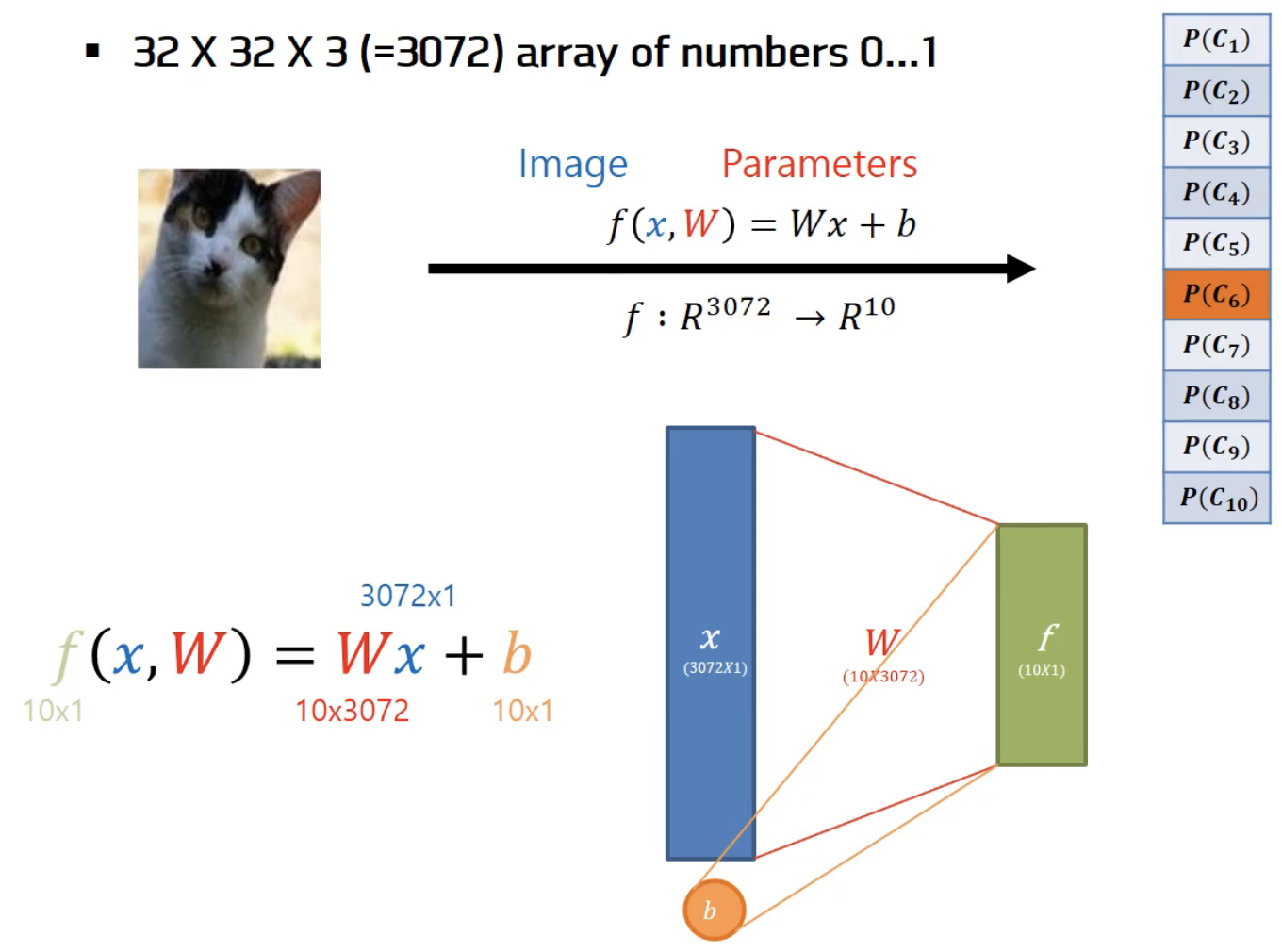
f(x, W) = Wx + b
- x : 입력이미지
- W : 파라미터(가중치,weight), 세타(theta)라고도 한다.
- b : 바이어스(bias), 입력과 직접 연결되지 않고 대신 데이터와 무관하게 특정 클래스에 우선권을 부여한다.
그리고 10개의 숫자를 출력하는데 이는 10개 카테고리의 스코어(각각의 클래스에 해당하는 확률)이다. 고양이의 스코어가 높다는 것은 입력x가 고양이일 확률이 높다는 것을 의미한다.
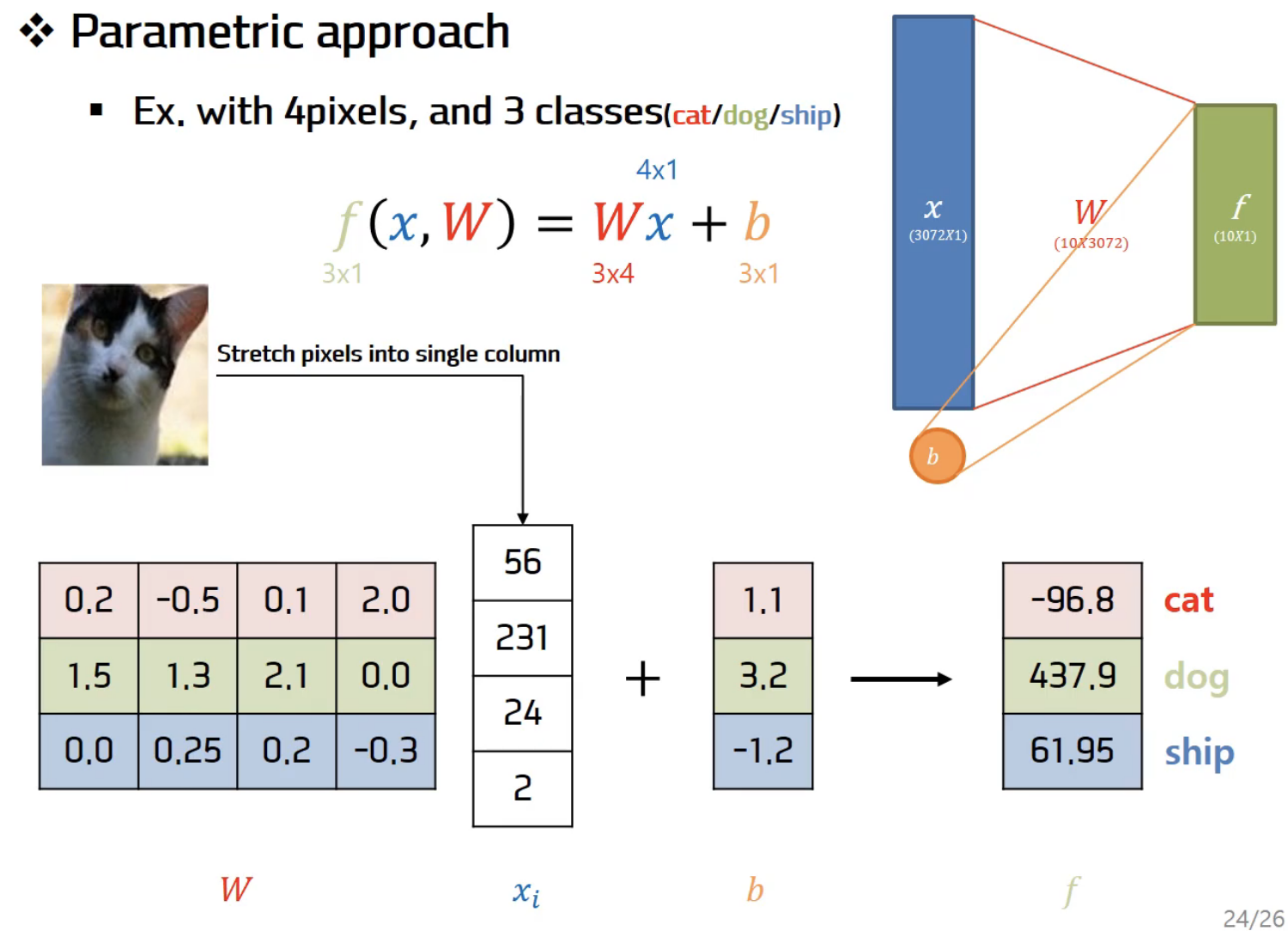
위 이미지에서 임의로 W, b값을 주었을 때 나온 결과값이 -96.8, 437.9, 61.95라면 저 고양이의 이미지는 dog로 결정된다.
계산 : ((0.2*56)+(-0.5*231)+(0.1*24)+(2.0*2))+1.1 = -96.8
앞서 KNN은 파라미터가 없었다. 그저 전체 트레이닝셋을 가지고 있었고 모든 트레이닝셋을 test time에 사용했다. 하지만 parametric approach에서는 트레이닝 데이터의 정보를 요약한다. 그리고 그 요약된 정보를 파라미터 W에 모아준다. 이런 방식을 사용하면 Test time에서 더이상 트레이닝 데이터가 필요하지 않는다. 그저 Test time에는 파라미터 W만 있으면 되는 것이다. 이 방법은 휴대폰과 같은 작은 디바이스에서 모델을 동작시켜야할 때 유용하다.
Linear classification은 템플릿 매칭과 유사하다. 가중치 행렬 W의 각 행은 각 이미지에 대한 템플릿으로 볼 수 있고 그 행 벡터와 이미지의 열벡터 간의 내적을 계산하는데, 여기에서 내적이란 결국 클래스 간 템플릿의 유사도를 측정하는 것과 유사함을 알 수 있다.
Visual Viewpoint
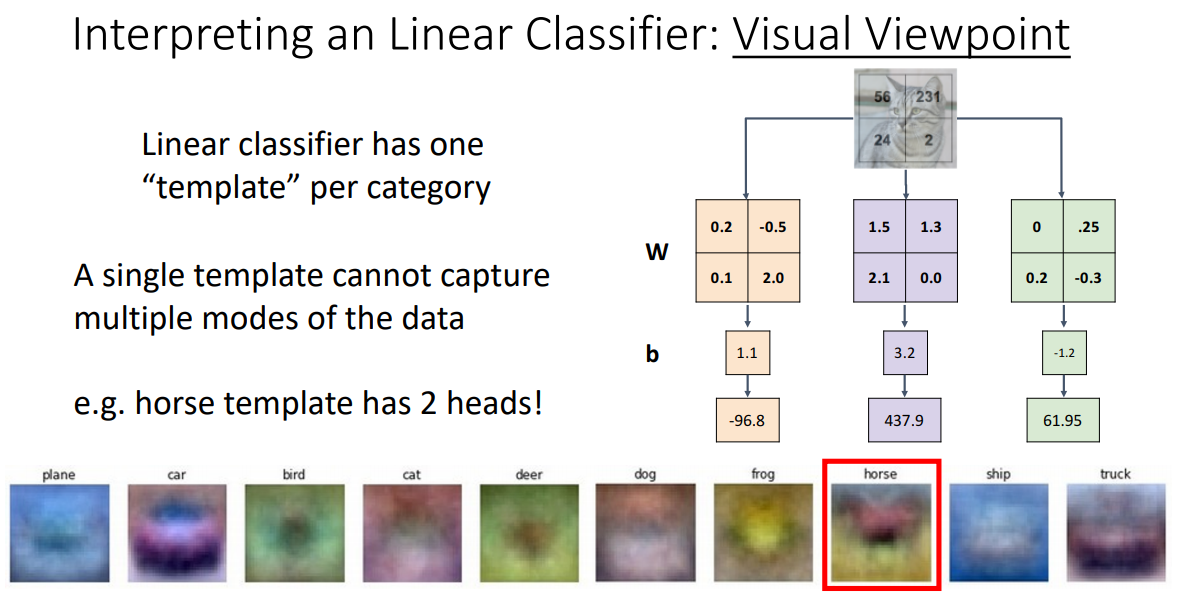
각각의 W들의 행을 이미지화함으로써 어떤 과정을 거치는지 알 수 있다. 위 이미지의 하단을 보면 각각의 클래스에 대한 템플릿 이미지를 볼 수 있다.
비행기는 전체적으로 푸른 빛을 띄고 있는데 이러한 특징이 비행기를 더 잘 찾을 수 있도록 도와준다고 해석할 수 있다. 하지만 말을 보면 약간 이상하다는 것을 느낄 수 있다. 말의 머리가 두개인 것처럼 보인다. 여기서 Linear classifier의 문제가 드러난다.
한 클래스 내에 다양한 특징들이 존재할 수 있지만, 모든 것들을 평균화시키기 때문에 클래스 당 하나의 템플릿밖에 허용하지 않으므로 이 방법이 최선이다.
Geometric Viewpoint
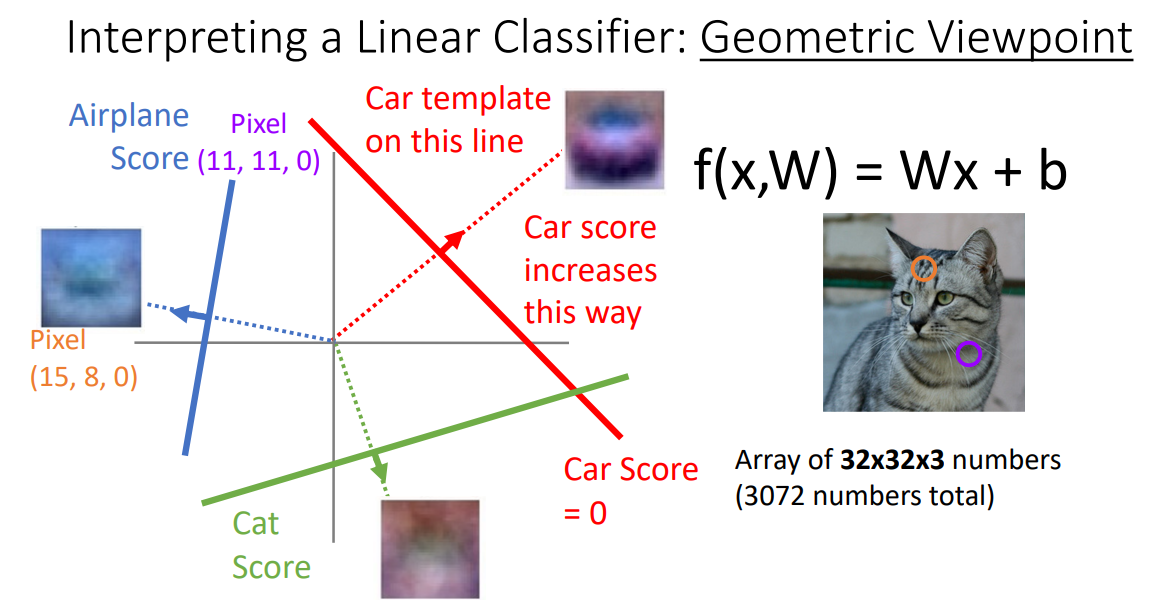
Linear classifier를 또 다른 관점으로 해석하자면 이미지를 고차원 공간의 한 점으로 보는 것이다. 각 이미지를 고차원 공간의 한 점이라고 생각했을 때 Linear classifier는 각 클래스를 구분시켜 주는 선형 결정 경계를 그어주는 역할을 한다.
하지만 Linear classifier로 분류하기 힘든 케이스가 많다.
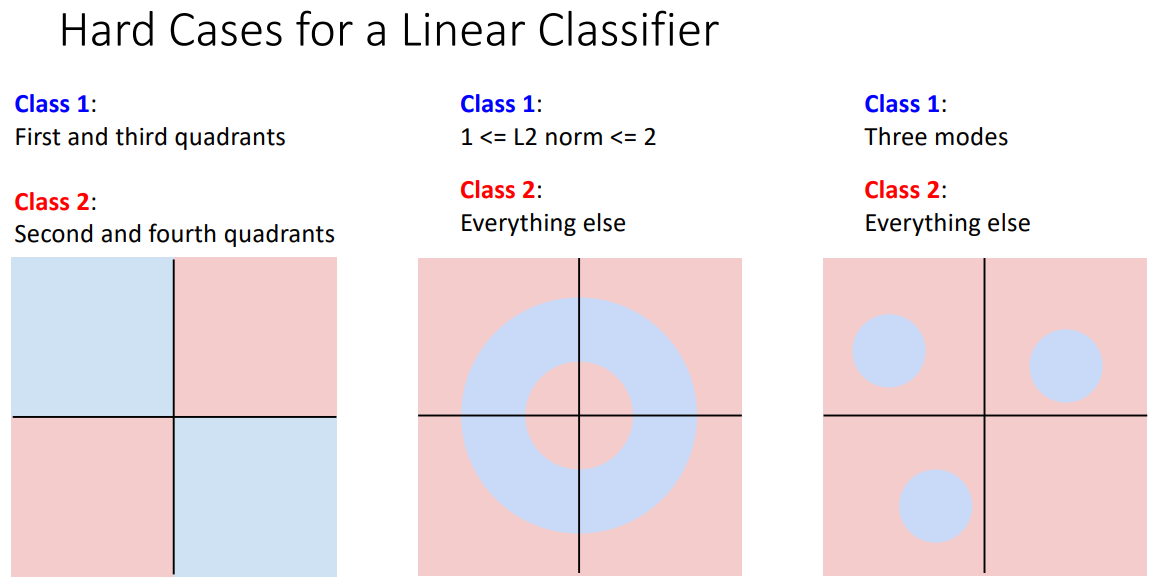
홀짝을 분류하는 것과 같은 반전성문제(parity problem)나 Multimodel data라면 한 클래스가 다양한 공간에 분포할 수 있는데 이러한 문제들은 일반적으로 Linear classification으로 풀기 힘들다.

위의 예시는 3개의 이미지에 랜덤으로 할당한 W를 가지고 있는 함수 F에 적용해본 것이다.
고양이 이미지는 개로, 자동차는 자동차로, 개구리는 트럭으로 예측이 된 것을 볼 수 있다.
W를 랜덤으로 주는 것이 아니라, 최적화방법론 등을 이용하여 optimize할 필요성이 있다는 것을 알 수 있다.
강의 동영상 : https://www.youtube.com/watch?v=f3gMzIt_d-A&feature=youtu.be
